
Jacobson radical
Encyclopedia
In mathematics
, more specifically ring theory
, a branch of abstract algebra
, the Jacobson radical of a ring
R is an ideal
which consists of those elements in R which annihilate
all simple
right R-modules
. It happens that substituting "left" in place of "right" in the definition yields the same ideal, and so the notion is left-right symmetric. The Jacobson radical of a ring is frequently denoted by J(R) or rad(R); however to avoid confusion with other radicals of rings
, the former notation will be preferred in this article. The Jacobson radical is named after Nathan Jacobson
, who was the first to study it for arbitrary rings in .
The Jacobson radical of a ring has numerous internal characterizations, including a few definitions which successfully extend the notion to rings without unity. The radical of a module
extends the definition of the Jacobson radical to include modules. The Jacobson radical plays a prominent role in many ring and module theoretic results, such as Nakayama's lemma.
, the Jacobson radical can be thought of as a collection of "bad" elements. In this case the "bad" property is that these elements annihilate all simple left and right modules of the ring. For purposes of comparison, consider the nilradical
of a commutative ring
, which consists of all elements which are nilpotent. In fact for any ring, the nilpotent elements in the center
of the ring are also in the Jacobson radical. So, for commutative rings, the nilradical is contained in the Jacobson radical.
The Jacobson radical is very similar to the nilradical in an intuitive sense. A weaker notion of being bad, weaker than being a zero divisor
, is being a non-unit (not invertible under multiplication). The Jacobson radical of a ring consists of elements which satisfy a stronger property than being merely a non-unit – in some sense, a member of the Jacobson radical must not "act as a unit" in any module
"internal to the ring." More precisely, a member of the Jacobson radical must project under the canonical homomorphism to the zero of every "right division ring" (each non-zero element of which has a right inverse
) internal to the ring in question. Concisely, it must belong to every maximal right ideal of the ring. These notions are of course imprecise, but at least explain why the nilradical of a commutative ring is contained in the ring's Jacobson radical.
In yet a simpler way, we may think of the Jacobson radical of a ring as method to "mod out bad elements" of the ring – that is, members of the Jacobson radical act as 0 in the quotient ring
, R/J(R). If N is the nilradical of commutative ring R, then the quotient ring R/N has no nilpotent elements. Similarly for any ring R, the quotient ring has J(R/J(R))={0} and so all of the "bad" elements in the Jacobson radical have been removed by modding out J(R). Elements of the Jacobson radical and nilradical can be therefore seen as generalizations of 0.
The following are equivalent characterizations of the Jacobson radical in rings with unity (characterizations for rings without unity are given immediately afterward):
For rings without unity it is possible for R=J(R), however the equation that J(R/J(R))={0} still holds. The following are equivalent characterizations of J(R) for rings without unity appear in :
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a branch of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the Jacobson radical of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
which consists of those elements in R which annihilate
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
all simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
right R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. It happens that substituting "left" in place of "right" in the definition yields the same ideal, and so the notion is left-right symmetric. The Jacobson radical of a ring is frequently denoted by J(R) or rad(R); however to avoid confusion with other radicals of rings
Radical of a ring
In ring theory, a branch of mathematics, a radical of a ring is an ideal of "bad" elements of the ring.The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is...
, the former notation will be preferred in this article. The Jacobson radical is named after Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
, who was the first to study it for arbitrary rings in .
The Jacobson radical of a ring has numerous internal characterizations, including a few definitions which successfully extend the notion to rings without unity. The radical of a module
Radical of a module
In mathematics, in the theory of modules, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical for rings. In many ways, it is the dual notion to that of the socle soc of M.-Definition:Let R be a ring and M a left...
extends the definition of the Jacobson radical to include modules. The Jacobson radical plays a prominent role in many ring and module theoretic results, such as Nakayama's lemma.
Intuitive discussion
As with other radicals of ringsRadical of a ring
In ring theory, a branch of mathematics, a radical of a ring is an ideal of "bad" elements of the ring.The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is...
, the Jacobson radical can be thought of as a collection of "bad" elements. In this case the "bad" property is that these elements annihilate all simple left and right modules of the ring. For purposes of comparison, consider the nilradical
Nilradical
In algebra, the nilradical of a commutative ring is the ideal consisting of the nilpotent elements of the ring. In the non-commutative ring case, more care is needed resulting in several related radicals.- Commutative rings :...
of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, which consists of all elements which are nilpotent. In fact for any ring, the nilpotent elements in the center
Center (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of the ring are also in the Jacobson radical. So, for commutative rings, the nilradical is contained in the Jacobson radical.
The Jacobson radical is very similar to the nilradical in an intuitive sense. A weaker notion of being bad, weaker than being a zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
, is being a non-unit (not invertible under multiplication). The Jacobson radical of a ring consists of elements which satisfy a stronger property than being merely a non-unit – in some sense, a member of the Jacobson radical must not "act as a unit" in any module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
"internal to the ring." More precisely, a member of the Jacobson radical must project under the canonical homomorphism to the zero of every "right division ring" (each non-zero element of which has a right inverse
Right inverse
A right inverse in mathematics may refer to:* A right inverse element with respect to a binary operation on a set* A right inverse function for a mapping between sets...
) internal to the ring in question. Concisely, it must belong to every maximal right ideal of the ring. These notions are of course imprecise, but at least explain why the nilradical of a commutative ring is contained in the ring's Jacobson radical.
In yet a simpler way, we may think of the Jacobson radical of a ring as method to "mod out bad elements" of the ring – that is, members of the Jacobson radical act as 0 in the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
, R/J(R). If N is the nilradical of commutative ring R, then the quotient ring R/N has no nilpotent elements. Similarly for any ring R, the quotient ring has J(R/J(R))={0} and so all of the "bad" elements in the Jacobson radical have been removed by modding out J(R). Elements of the Jacobson radical and nilradical can be therefore seen as generalizations of 0.
Equivalent characterizations
The Jacobson radical of a ring has various internal and external characterizations. The following equivalences appear in many noncommutative algebra texts such as , , and .The following are equivalent characterizations of the Jacobson radical in rings with unity (characterizations for rings without unity are given immediately afterward):
- J(R) equals the intersection of all maximal right idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
within the ring. It is also true that J(R) equals the intersection of all maximal left ideals within the ring. These characterizations are internal to the ring, since one only needs to find the maximal right ideals of the ring. For example, if a ring is localLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, and has a unique maximal right ideal, then this unique maximal right ideal is an ideal because it is exactly J(R). Maximal ideals are in a sense easier to look for than annihilators of modules. This characterization is deficient, however, because it does not prove useful when working computationally with J(R). The left-right symmetry of these two definitions is remarkable and has various interesting consequences. This symmetry stands in contrast to the lack of symmetry in the socles of R, for it may happen that soc(RR) is not equal to soc(RR). However, J(R) is not necessarily equal to the intersection of all maximal (double-sided) ideals within R. For instance, if V is a countable direct sum of copies of a field k and R=End(V) (the ring of endomorphisms of V as a k-module), then J(R)=0 because R is known to be von Neumann regular, but there is exactly one maximal double-sided ideal in R consisting of endomorphisms with finite-dimensional image.
- J(R) equals the sum of all superfluous right ideals (or symmetrically, the sum of all superfluous left ideals) of R. Comparing this with the previous definition, the sum of superfluous right ideals equals the intersection of maximal right ideals. This phenomenon is reflected dually for the right socle of R: soc(RR) is both the sum of minimal right ideals and the intersection of essential right ideals. In fact, these two astounding relationships hold for the radicals and socles of modules in general.
- As defined in the introduction, J(R) equals the intersection of all annihilatorsAnnihilator (ring theory)In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of simpleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
right R-modules, however it is also true that it is the intersection of annihilators of simple left modules. An ideal that is the annihilator of a simple module is known as a primitive idealPrimitive idealIn mathematics, a left primitive ideal in ring theory is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that left and right primitive ideals are always two-sided ideals....
, and so a reformulation of this states that the Jacobson radical is the intersection of all primitive ideals. Although this characterization is not useful computationally, or as useful as the previous two characterizations in aiding intuition, it is useful in studying modules over rings. For instance, if U is right R-module, and V is a maximal submodule of U, U·J(R) is contained in V, where U·J(R) denotes all products of elements of J(R) (the "scalars") with elements in U, on the right. This follows from the fact that the quotient moduleQuotient moduleIn abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
, U/V is simple and hence annihilated by J(R). As another example, this result motivates Nakayama's lemma.
- J(R) is the unique right ideal of R maximal with the property that every element is right quasiregularQuasiregular elementIn mathematics, specifically ring theory, the notion of quasiregularity provides a computationally convenient way to work with the Jacobson radical of a ring. Intuitively, quasiregularity captures what it means for an element of a ring to be "bad"; that is, have undesirable properties...
. Alternatively, one could replace "right" with "left" in the previous sentence. This characterization of the Jacobson radical is useful both computationally and in aiding intuition. Furthermore, this characterization is useful in studying modules over a ring. Nakayama's lemma is perhaps the most well-known instance of this. Although every element of the J(R) is necessarily quasiregularQuasiregular elementIn mathematics, specifically ring theory, the notion of quasiregularity provides a computationally convenient way to work with the Jacobson radical of a ring. Intuitively, quasiregularity captures what it means for an element of a ring to be "bad"; that is, have undesirable properties...
, not every quasiregular element is necessarily a member of J(R).
- While not every quasiregular element is in J(R), it can be shown that y is in J(R) if and only if xy is left quasiregular for all x in R.
For rings without unity it is possible for R=J(R), however the equation that J(R/J(R))={0} still holds. The following are equivalent characterizations of J(R) for rings without unity appear in :
- The notion of left quasiregularity can be generalized in the following way. Call an element a in R left generalized quasiregular if there exists c in R such that c+a-ca= 0. Then J(R) consists of every element a for which ra is left generalized quasiregular for all r in R. It can be checked that this definition coincides with the previous quasiregular definition for rings with unity.
- For a ring without unity, the definition of a left simple moduleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
M is amended by adding the condition that R•M ≠ 0. With this understanding, J(R) may be defined as the intersection of all simple left R modules, or just R if there are no simple left R modules. Rings without unity with no simple modules do exist, in which case R=J(R), and the ring is called a radical ring. By using the generalized quasiregular characterization of the radical, it is clear that if one finds a ring with J(R) nonzero, then J(R) is a radical ring when considered as a ring without unity.
Examples
- Rings for which J(R) is {0} are called semiprimitive ringSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
s, or sometimes "Jacobson semisimple rings". The Jacobson radical of any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, any von Neumann regular ringVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
and any left or right primitive ringPrimitive ringIn the branch of abstract algebra known as ring theory, a left primitive ring is a ring which has a faithful simple left module. Well known examples include endomorphism rings of vector spaces and Weyl algebras over fields of characteristic zero.- Definition :...
is {0}. The Jacobson radical of the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is {0}. - The Jacobson radical of the ring Z/12Z (see modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
) is 6Z/12Z, which is the intersection of the maximal ideals 2Z/12Z and 3Z/12Z. - If K is a field and R is the ring of all upper triangular n-by-n matrices with entries in K, then J(R) consists of all upper triangular matrices with zeros on the main diagonal.
- If K is a field and R = K
X1, ..., Xn is a ring of formal power series Formal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, then J(R) consists of those power series whose constant term is zero. More generally: the Jacobson radical of every local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
is the unique maximal ideal of the ring, which consists precisely of the ring's non-units. - Start with a finite, acyclic quiverQuiver (mathematics)In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
Γ and a field K and consider the quiver algebra KΓ (as described in the quiver articleQuiver (mathematics)In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
). The Jacobson radical of this ring is generated by all the paths in Γ of length ≥ 1. - The Jacobson radical of a C*-algebra is {0}. This follows from the Gelfand–Naimark theoremGelfand–Naimark theoremIn mathematics, the Gelfand–Naimark theorem states that an arbitrary C*-algebra A is isometrically *-isomorphic to a C*-algebra of bounded operators on a Hilbert space...
and the fact for a C*-algebra, a topologically irreducible *-representation on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is algebraically irreducible, so that its kernel is a primitive ideal in the purely algebraic sense (see spectrum of a C*-algebra).
Properties
- If R is unital and is not the trivial ring {0}, the Jacobson radical is always distinct from R since rings with unity always have maximal right ideals. However, some important theorems and conjectures in ring theory consider the case when J(R) = R - "If R is a nil ring (that is, each of its elements is nilpotent), is the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x] equal to its Jacobson radical?" is equivalent to the open Köthe conjecture.
- The Jacobson radical of the ring R/J(R) is zero. Rings with zero Jacobson radical are called semiprimitive ringSemiprimitive ringIn mathematics, especially in the area of algebra known as ring theory, a semiprimitive ring is a type of ring more general than a semisimple ring, but where simple modules still provide enough information about the ring. Important rings such as the ring of integers are semiprimitive, and an...
s.
- A ring is semisimpleSemisimpleIn mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
if and only if it is ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
and its Jacobson radical is zero.
- If f : R → S is a surjective ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
, then f(J(R)) ⊆ J(S).
- If M is a finitely generated left R-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with J(R)M = M, then M = 0 (Nakayama's lemma).
- J(R) contains all central nilpotent elements, but contains no idempotentIdempotenceIdempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application...
elements except for 0.
- J(R) contains every nil idealNil idealIn mathematics, more specifically ring theory, an ideal of a ring is said to be a nil ideal if each of its elements is nilpotent. The nilradical of a commutative ring is an example of a nil ideal; in fact, it is the ideal of the ring maximal with respect to the property of being nil...
of R. If R is left or right ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
, then J(R) is a nilpotent idealNilpotent idealIn mathematics, more specifically ring theory, an ideal, I, of a ring is said to be a nilpotent ideal, if there exists a natural number k such that Ik = 0. By Ik, it is meant the additive subgroup generated by the set of all products of k elements in I...
. This can actually be made stronger: If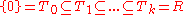 is a composition series for the right R-module R (such a series is sure to exist if R is right artinian, and there is a similar left composition series if R is left artinian), then
is a composition series for the right R-module R (such a series is sure to exist if R is right artinian, and there is a similar left composition series if R is left artinian), then  . (Proof: Since the factors
. (Proof: Since the factors  are simple right R-modules, right multiplication by any element of J(R) annihilates these factors. In other words,
are simple right R-modules, right multiplication by any element of J(R) annihilates these factors. In other words,  , whence
, whence  . Consequently, induction over i shows that all nonnegative integers i and u (for which the following makes sense) satisfy
. Consequently, induction over i shows that all nonnegative integers i and u (for which the following makes sense) satisfy 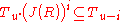 . Applying this to u = i = k yields the result.) Note, however, that in general the Jacobson radical need not consist of only the nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
. Applying this to u = i = k yields the result.) Note, however, that in general the Jacobson radical need not consist of only the nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements of the ring.
- If R is commutative and finitely generated as a Z-module, then J(R) is equal to the nilradical of R.
- In a right Noetherian ring, J(R) is a superfluous right ideal.
See also
- Nilradical
- Radical of a moduleRadical of a moduleIn mathematics, in the theory of modules, the radical of a module is a component in the theory of structure and classification. It is a generalization of the Jacobson radical for rings. In many ways, it is the dual notion to that of the socle soc of M.-Definition:Let R be a ring and M a left...
- Radical of an idealRadical of an idealIn commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
- Frattini subgroupFrattini subgroupIn mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...

