
Fundamental unit (number theory)
Encyclopedia
In algebraic number theory
, a fundamental unit is a generator for the torsion-free unit group of the ring of integers
of a number field, when that group is infinite cyclic. See also Dirichlet's unit theorem
.
For rings of the form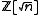 , the fundamental unit has the form
, the fundamental unit has the form  where (x,y) is the smallest nontrivial solution to Pell's equation
where (x,y) is the smallest nontrivial solution to Pell's equation
x2 - ny2 = 1 or x2 - ny2 = -1. (For example, if n is a prime that is 1 mod 4 then
the fundamental unit comes from a solution of the second equation.)
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, a fundamental unit is a generator for the torsion-free unit group of the ring of integers
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
of a number field, when that group is infinite cyclic. See also Dirichlet's unit theorem
Dirichlet's unit theorem
In mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
.
For rings of the form
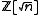 , the fundamental unit has the form
, the fundamental unit has the form  where (x,y) is the smallest nontrivial solution to Pell's equation
where (x,y) is the smallest nontrivial solution to Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
x2 - ny2 = 1 or x2 - ny2 = -1. (For example, if n is a prime that is 1 mod 4 then
the fundamental unit comes from a solution of the second equation.)

