
Monodromy theorem
Encyclopedia
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the monodromy theorem is an important result about analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of a complex-analytic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
to a larger set. The idea is that one can extend a complex-analytic function (from here on called simply analytic function) along curves starting in the original domain of the function and ending in the larger set. A potential problem of this analytic continuation along a curve strategy is there are usually many curves which end up at the same point in the larger set. The monodromy theorem gives sufficient conditions for analytic continuation to give the same value at a given point regardless of the curve used to get there, so that the resulting extended analytic function is well-defined and single-valued.
Before stating this theorem it is necessary to define analytic continuation along a curve and study its properties.
Analytic continuation along a curve
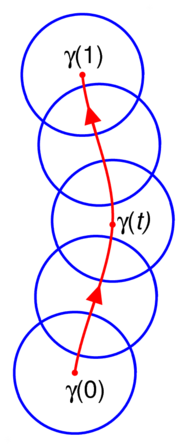
The definition of analytic continuation along a curve is a bit technical, but the basic idea is that one starts with an analytic function defined around a point, and one extends that function along a curve via analytic functions defined on small overlapping disks covering that curve.Formally, consider a curve (a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
)
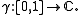 Let
Let  be an analytic function defined on an open disk
be an analytic function defined on an open disk 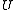 centered at
centered at 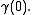 An analytic continuation of the pair
An analytic continuation of the pair 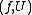 along
along 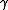 is a collection of pairs
is a collection of pairs 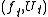 for
for 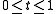 such that
such that
-
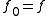 and
and 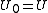
- For each
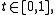
 is an open disk centered at
is an open disk centered at 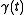 and
and  is an analytic function
is an analytic function - For each
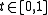 there exists
there exists 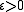 such that for all
such that for all 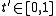 with
with 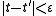 one has that
one has that 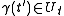 (which implies that
(which implies that  and
and  have a non-empty intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
have a non-empty intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
) and the functions and
and 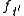 coincide on the intersection
coincide on the intersection 
Properties of analytic continuation along a curve
Analytic continuation along a curve is essentially unique, in the sense that given two analytic continuations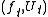 and
and 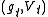
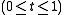 of
of  along
along 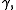 the functions
the functions 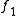 and
and 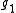 coincide on
coincide on 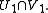 Informally, this says that any two analytic continuations of
Informally, this says that any two analytic continuations of 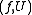 along
along 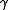 will end up with the same values in a neighborhood of
will end up with the same values in a neighborhood of 
If the curve
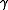 is closed (that is,
is closed (that is,  ), one need not have
), one need not have 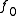 equal
equal 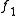 in a neighborhood of
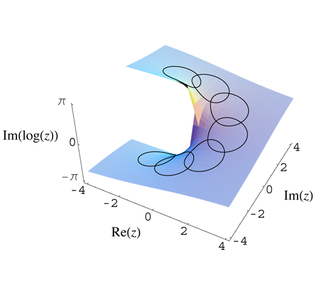
in a neighborhood of  For example, if one starts at a point
For example, if one starts at a point 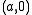 with
with  and the complex logarithm
and the complex logarithmComplex logarithm
In complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
defined in a neighborhood of this point, and one lets
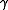 be the circle of radius
be the circle of radius  centered at the origin (traveled counterclockwise from
centered at the origin (traveled counterclockwise from 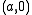 ), then by doing an analytic continuation along this curve one will end up with a value of the logarithm at
), then by doing an analytic continuation along this curve one will end up with a value of the logarithm at 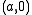 which is
which is 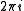 plus the original value (see the second illustration on the right).
plus the original value (see the second illustration on the right).Monodromy theorem

Indeed, one can consider, as in the previous section, the complex logarithm defined in a neighborhood of a point
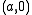 and the circle centered at the origin and radius
and the circle centered at the origin and radius 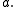 Then, it is possible to travel from
Then, it is possible to travel from  to
to  in two ways, counterclockwise, on the upper half-plane arc of this circle, and clockwise, on the lower half-plane arc. The values of the logarithm at
in two ways, counterclockwise, on the upper half-plane arc of this circle, and clockwise, on the lower half-plane arc. The values of the logarithm at  obtained by analytic continuation along these two arcs will differ by
obtained by analytic continuation along these two arcs will differ by 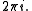
If, however, one can continuously deform one of the curves into another while keeping the starting points and ending points fixed, and analytic continuation is possible on each of the intermediate curves, then the analytic continuations along the two curves will yield the same results at their common endpoint. This is called the monodromy theorem and its statement is made precise below.
- Let
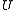 be an open disk in the complex plane centered at a point
be an open disk in the complex plane centered at a point 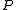 and
and 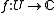 be a complex-analytic function. Let
be a complex-analytic function. Let 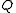 be another point in the complex plane. If there exists a family of curves
be another point in the complex plane. If there exists a family of curves 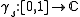 with
with 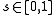 such that
such that 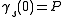 and
and 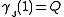 for all
for all 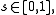 the function
the function 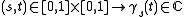 is continuous, and for each
is continuous, and for each 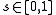 it is possible to do an analytic continuation of
it is possible to do an analytic continuation of 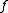 along
along  then the analytic continuations of
then the analytic continuations of 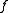 along
along 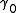 and
and 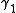 will yield the same values at
will yield the same values at 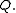
The monodromy theorem makes it possible to extend an analytic function to a larger set via curves connecting a point in the original domain of the function to points in the larger set. The theorem below which states that is also called the monodromy theorem.
- Let
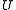 be an open disk in the complex plane centered at a point
be an open disk in the complex plane centered at a point 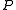 and
and 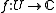 be a complex-analytic function. If
be a complex-analytic function. If 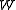 is an open simply-connected set containing
is an open simply-connected set containing  , and it is possible to perform an analytic continuation of
, and it is possible to perform an analytic continuation of 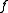 on any curve contained in
on any curve contained in 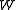 which starts at
which starts at 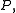 then
then 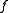 admits a direct analytic continuation to
admits a direct analytic continuation to 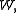 meaning that there exists a complex-analytic function
meaning that there exists a complex-analytic function 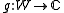 whose restriction to
whose restriction to 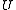 is
is 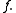
External links
- Monodromy theorem at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Monodromy theorem at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Monodromy theorem at the Encyclopaedia of MathematicsEncyclopaedia of MathematicsThe Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....

