Yield surface
Encyclopedia
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex
and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point
and the material is said to have become plastic
. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity
, though not in some models of viscoplasticity
.
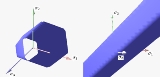
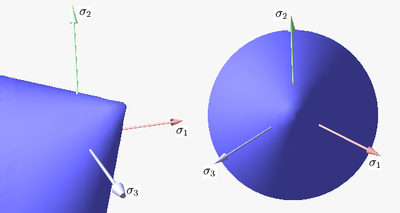
The yield surface is usually expressed in terms of (and visualized in) a three-dimensional principal stress space (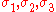
), a two- or three-dimensional space spanned by stress invariants (
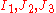) or a version of the three-dimensional Haigh–Westergaard stress space
. Thus we may write the equation of the yield surface (that is, the yield function) in the forms:
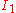) of the Cauchy stress (
), and the second and third principal invariants (
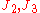) of the deviatoric part (
) of the Cauchy stress are defined as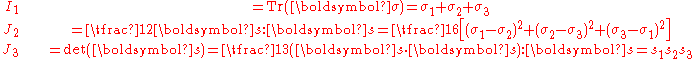
where (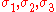
) are the principal values of 
, (
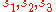) are the principal values of 
, and
where
is the identity matrix.
A related set of quantities, (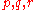
), are usually used to describe yield surfaces for cohesive frictional materials such as rocks, soils, and ceramics. These are defined as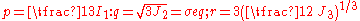
where
is the equivalent stress. However, the possibility of negative values of 
and the resulting imaginary 
makes the use of these quantities problematic in practice.
Another related set of widely used invariants is (
) which describe a cylindrical coordinate system
(the Haigh–Westergaard coordinates). These are defined as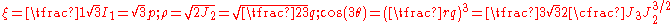
The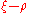
plane is also called the Rendulic plane. The angle 
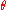is called the Lode angle and the relation between 
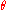and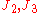 
was first given by Nayak and Zienkiewicz in 1972
The principal stresses and the Haigh–Westergaard coordinates are related by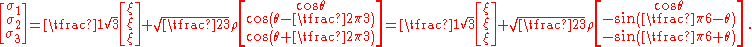
A different definition of the Lode angle can also be found in the literature: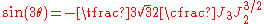
in which case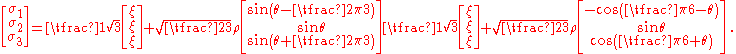
Whatever definition is chosen, the angle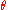
varies between -30 degrees to +30 degrees.
. It is also referred as also known as the maximum shear stress theory (MSST) and the Tresca–Guest (TG) criterion. In terms of the principal stresses the Tresca criterion is expressed as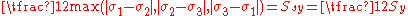
Where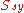
is the yield strength in shear, and 
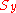is the tensile yield strength.
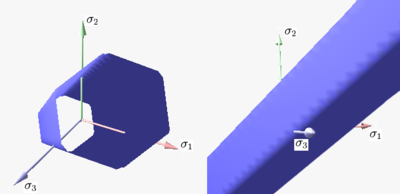
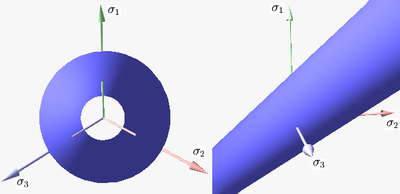
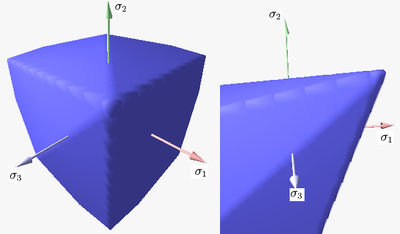
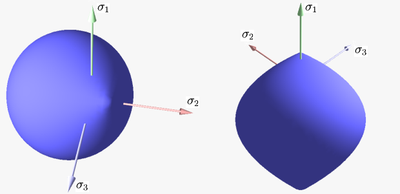
Figure 1 shows the Tresca–Guest yield surface in the three-dimensional space of principal stresses. It is a prism
of six sides and having infinite length. This means that the material remains elastic when all three principal stresses are roughly equivalent (a hydrostatic pressure), no matter how much it is compressed or stretched. However, when one of principal stresses becomes smaller (or larger) than the others the material is subject to shearing. In such situations, if the shear stress reaches the yield limit then the material enters the plastic domain. Figure 2 shows the Tresca–Guest yield surface in two-dimensional stress space, it is a cross section of the prism along the
plane.
>
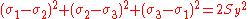
where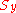
is the yield strength in uniaxial tension.
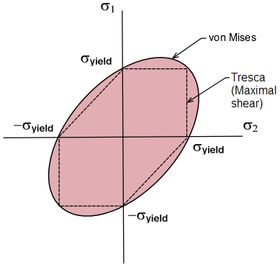
Figure 3 shows the von Mises yield surface in the three-dimensional space of principal stresses. It is a circular cylinder
of infinite length with its axis inclined at equal angles to the three principal stresses. Figure 4 shows the von Mises yield surface in two-dimensional space compared with Tresca–Guest criterion. A cross section of the von Mises cylinder on the plane of
produces the elliptical
shape of the yield surface.
>
, soil
or granular material
s. The Mohr–Coulomb yield criterion may be expressed as: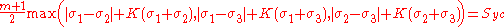
where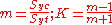
and the parameters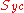
and 
are the yield (failure) stresses of the material in uniaxial compression and tension, respectively. The formula reduces to the Tresca criterion if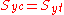 
.
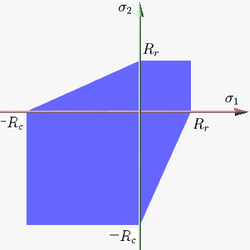
Figure 5 shows Mohr–Coulomb yield surface in the three-dimensional space of principal stresses. It is a conical prism and
determines the inclination angle of conical surface. Figure 6 shows Mohr–Coulomb yield surface in two-dimensional stress space. It is a cross section of this conical prism on the plane of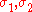 
.
>
where both normal and shear stresses can determine failure. The Drucker–Prager yield criterion may be expressed as
where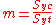
and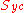
, 
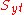are the uniaxial yield stresses in compression and tension respectively. The formula reduces to the von Mises equation if 
.
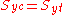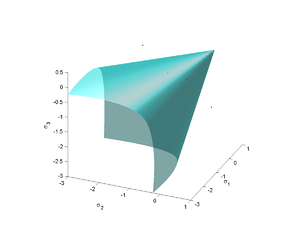
Figure 7 shows Drucker–Prager yield surface in the three-dimensional space of principal stresses. It is a regular cone
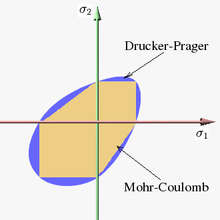
. Figure 8 shows Drucker–Prager yield surface in two-dimensional space. The ellipsoidal-shaped elastic domain is a cross section of the cone on the plane of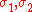
; here it is shown enclosing the elastic domain for the Mohr–Coulomb yield criterion, although the converse scenario is also possible.
>
that uses three parameters, and has additional terms for materials that yield under hydrostatic compression.
In terms of the principal stresses, this yield criterion may be expressed as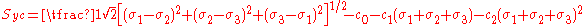
where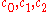
are material constants. The additional parameter 
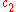gives the yield surface an ellipsoidal
cross section when viewed from a direction perpendicular to its axis. If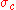
is the yield stress in uniaxial compression, 
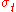is the yield stress in uniaxial tension, and 
is the yield stress in biaxial compression, the parameters can be expressed as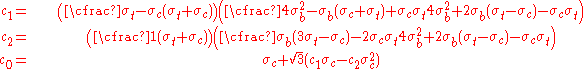
>
yield criteria.
The yield criterion has the functional form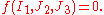
However, it is more commonly expressed in Haigh–Westergaard coordinates as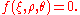
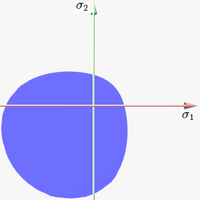
The cross-section of the surface when viewed along its axis is a smoothed triangle (unlike Mohr–Coulumb). The Willam–Warnke yield surface is convex and has unique and well defined first and second derivatives on every point of its surface. Therefore the Willam–Warnke model is computationally robust and has been used for a variety of cohesive-frictional materials.
>
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
and the material is said to have become plastic
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
, though not in some models of viscoplasticity
Viscoplasticity
Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied...
.
The yield surface is usually expressed in terms of (and visualized in) a three-dimensional principal stress space (
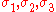), a two- or three-dimensional space spanned by stress invariants (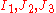) or a version of the three-dimensional Haigh–Westergaard stress spaceStress space
In continuum mechanics, Haigh–Westergaard stress space, or simply stress space is a 3-dimensional space in which the three spatial axes represent the three principal stresses for a body subject to stress....
. Thus we may write the equation of the yield surface (that is, the yield function) in the forms:
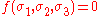where 
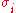are the principal stresses.
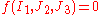where 
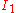is the first principal invariant of the Cauchy stress and 
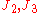are the second and third principal invariants of the deviatoric part of the Cauchy stress.
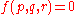where 
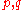are scaled versions of 
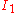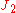and 
and 
is a function of 
.
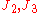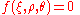where 
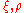are scaled versions of 
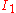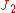and 
, and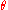 
is the Lode angle.
Invariants used to describe yield surfaces
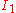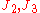The first principal invariant () of the Cauchy stress (), and the second and third principal invariants () of the deviatoric part () of the Cauchy stress are defined as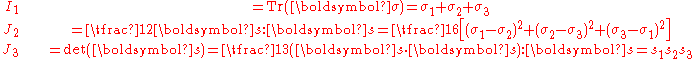where (
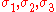) are the principal values of , (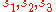) are the principal values of , andwhere
is the identity matrix.A related set of quantities, (
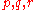), are usually used to describe yield surfaces for cohesive frictional materials such as rocks, soils, and ceramics. These are defined as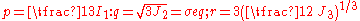where
is the equivalent stress. However, the possibility of negative values of and the resulting imaginary makes the use of these quantities problematic in practice.Another related set of widely used invariants is (
) which describe a cylindrical coordinate systemCylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
(the Haigh–Westergaard coordinates). These are defined as
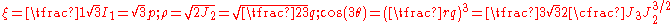
The
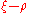plane is also called the Rendulic plane. The angle 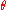is called the Lode angle and the relation between 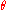and 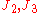was first given by Nayak and Zienkiewicz in 1972 The principal stresses and the Haigh–Westergaard coordinates are related by
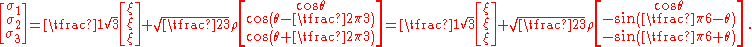
A different definition of the Lode angle can also be found in the literature:
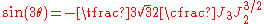
in which case
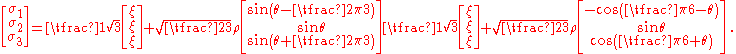
Whatever definition is chosen, the angle
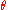varies between -30 degrees to +30 degrees.Examples of yield surfaces
There are several different yield surfaces known in engineering, and those most popular are listed below.Tresca yield surface
The Tresca yield criterion is taken to be the work of Henri TrescaHenri Tresca
Henri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
. It is also referred as also known as the maximum shear stress theory (MSST) and the Tresca–Guest (TG) criterion. In terms of the principal stresses the Tresca criterion is expressed as
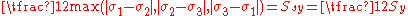
Where
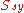is the yield strength in shear, and 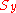is the tensile yield strength.Figure 1 shows the Tresca–Guest yield surface in the three-dimensional space of principal stresses. It is a prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
of six sides and having infinite length. This means that the material remains elastic when all three principal stresses are roughly equivalent (a hydrostatic pressure), no matter how much it is compressed or stretched. However, when one of principal stresses becomes smaller (or larger) than the others the material is subject to shearing. In such situations, if the shear stress reaches the yield limit then the material enters the plastic domain. Figure 2 shows the Tresca–Guest yield surface in two-dimensional stress space, it is a cross section of the prism along the
plane.von Mises yield surface
The von Mises yield criterion is expressed in the principal stresses as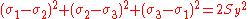where
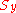is the yield strength in uniaxial tension.Figure 3 shows the von Mises yield surface in the three-dimensional space of principal stresses. It is a circular cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
of infinite length with its axis inclined at equal angles to the three principal stresses. Figure 4 shows the von Mises yield surface in two-dimensional space compared with Tresca–Guest criterion. A cross section of the von Mises cylinder on the plane of
produces the ellipticalEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
shape of the yield surface.
Mohr–Coulomb yield surface
The Mohr–Coulomb yield (failure) criterion is similar to the Tresca criterion, with additional provisions for materials with different tensile and compressive yield strengths. This model is often used to model concreteConcrete
Concrete is a composite construction material, composed of cement and other cementitious materials such as fly ash and slag cement, aggregate , water and chemical admixtures.The word concrete comes from the Latin word...
, soil
Soil
Soil is a natural body consisting of layers of mineral constituents of variable thicknesses, which differ from the parent materials in their morphological, physical, chemical, and mineralogical characteristics...
or granular material
Granular material
A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact . The constituents that compose granular material must be large enough such that they are not subject to thermal motion fluctuations...
s. The Mohr–Coulomb yield criterion may be expressed as:
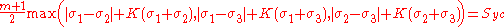
where
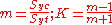
and the parameters
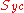and are the yield (failure) stresses of the material in uniaxial compression and tension, respectively. The formula reduces to the Tresca criterion if 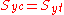.Figure 5 shows Mohr–Coulomb yield surface in the three-dimensional space of principal stresses. It is a conical prism and
determines the inclination angle of conical surface. Figure 6 shows Mohr–Coulomb yield surface in two-dimensional stress space. It is a cross section of this conical prism on the plane of .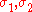
Drucker–Prager yield surface
The Drucker–Prager yield criterion is similar to the von Mises yield criterion, with provisions for handling materials with differing tensile and compressive yield strengths. This criterion is most often used for concreteConcrete
Concrete is a composite construction material, composed of cement and other cementitious materials such as fly ash and slag cement, aggregate , water and chemical admixtures.The word concrete comes from the Latin word...
where both normal and shear stresses can determine failure. The Drucker–Prager yield criterion may be expressed as
where
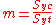
and
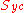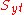, are the uniaxial yield stresses in compression and tension respectively. The formula reduces to the von Mises equation if 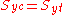.Figure 7 shows Drucker–Prager yield surface in the three-dimensional space of principal stresses. It is a regular cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
. Figure 8 shows Drucker–Prager yield surface in two-dimensional space. The ellipsoidal-shaped elastic domain is a cross section of the cone on the plane of
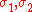; here it is shown enclosing the elastic domain for the Mohr–Coulomb yield criterion, although the converse scenario is also possible.Bresler–Pister yield surface
The Bresler–Pister yield criterion is an extension of the Drucker Prager yield criterionDrucker Prager yield criterion
The Drucker–Prager yield criterion is a pressure-dependent model for determining whether a material has failed or undergone plastic yielding. The criterion was introduced to deal with the plastic deformation of soils...
that uses three parameters, and has additional terms for materials that yield under hydrostatic compression.
In terms of the principal stresses, this yield criterion may be expressed as
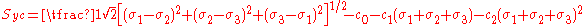
where
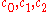are material constants. The additional parameter 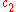gives the yield surface an ellipsoidalEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
cross section when viewed from a direction perpendicular to its axis. If
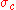is the yield stress in uniaxial compression, 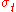is the yield stress in uniaxial tension, and is the yield stress in biaxial compression, the parameters can be expressed as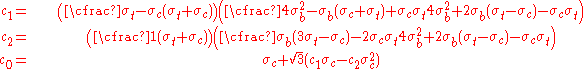Willam–Warnke yield surface
The Willam–Warnke yield criterion is a three-parameter smoothed version of the Mohr–Coulomb yield criterion that has similarities in form to the Drucker–Prager and Bresler–PisterBresler Pister yield criterion
The Bresler-Pister yield criterion is a function that was originally devised to predict the strength of concrete under multiaxial stress states...
yield criteria.
The yield criterion has the functional form
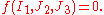
However, it is more commonly expressed in Haigh–Westergaard coordinates as
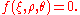
The cross-section of the surface when viewed along its axis is a smoothed triangle (unlike Mohr–Coulumb). The Willam–Warnke yield surface is convex and has unique and well defined first and second derivatives on every point of its surface. Therefore the Willam–Warnke model is computationally robust and has been used for a variety of cohesive-frictional materials.
See also
- Yield (engineering)Yield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
- Plasticity (physics)Plasticity (physics)In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
- StressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- Henri TrescaHenri TrescaHenri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
- von Mises stressVon Mises stressThe von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J_2 reaches a critical value k. For this reason, it is sometimes called the J_2-plasticity or J_2 flow theory. It is part of a plasticity theory that applies best to ductile...
- Mohr–Coulomb theory
- StrainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
- Strain tensor
- Stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
- Stress concentrationStress concentrationA stress concentration is a location in an object where stress is concentrated. An object is strongest when force is evenly distributed over its area, so a reduction in area, e.g. caused by a crack, results in a localized increase in stress...
- 3-D elasticity