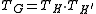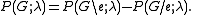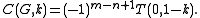Tutte polynomial
Encyclopedia

Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in two variables which plays an important role in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
. It is defined for every undirected graph and contains information about how the graph is connected.
The importance of the Tutte polynomial
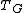 comes from the information it contains about
comes from the information it contains about 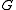 . Though originally studied in algebraic graph theory
. Though originally studied in algebraic graph theoryAlgebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
as a generalisation of counting problems related to graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
and nowhere-zero flow, it contains several famous other specialisations from other sciences such as the Jones polynomial from knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
and the partition functions of the Potts model
Potts model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
from statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
. It is also the source of several central computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
s in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
.
The Tutte polynomial has several equivalent definitions. It is equivalent to Whitney’s rank polynomial, Tutte’s own dichromatic polynomial and Fortuin–Kasteleyn’s random cluster model under simple transformations. It is essentially a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the number of edge sets of a given size and connected components, with immediate generalisations to matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s. It is also the most general graph invariant that can be defined by a deletion–contraction recurrence. Several textbooks about graph theory and matroid theory devote entire chapters to it.
Definitions
For an undirected graph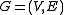 one may define the Tutte polynomial as
one may define the Tutte polynomial as
Here,
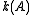 denotes the number of connected component
denotes the number of connected componentConnected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
s of the graph
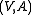 .
.In this definition it is clear that
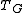 is well-defined and a polynomial in
is well-defined and a polynomial in  and
and  . The same definition can be given using slightly different notation by letting
. The same definition can be given using slightly different notation by letting  denote the rank
denote the rankRank (graph theory)
In graph theory, a branch of mathematics, the rank of an undirected graph is defined as the number , where is the number of vertices and is the number of connected components of the graph...
of the graph
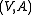 . Then the Whitney rank generating function is defined as
. Then the Whitney rank generating function is defined as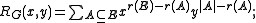
the two functions are equivalent under a simple change of variables:
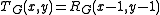 . Tutte’s dichromatic polynomial
. Tutte’s dichromatic polynomial 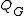 is the result of another simple transformation:
is the result of another simple transformation: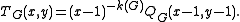
Tutte’s original definition of
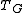 is equivalent but less easily stated. For connected
is equivalent but less easily stated. For connected 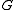 we set
we set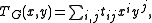
where
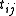 denotes the number of spanning tree
denotes the number of spanning treeSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s of “internal activity
 and external activity
and external activity 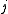 .”
.”A third definition uses a deletion–contraction recurrence. The edge contraction
Edge contraction
In graph theory, an edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors...
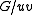 of graph
of graph 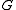 is the graph obtained by merging the vertices
is the graph obtained by merging the vertices  and
and  and removing the edge
and removing the edge 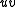 . We write
. We write 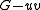 for the graph where the edge
for the graph where the edge  is merely removed. Then the Tutte polynomial is defined by the recurrence relation
is merely removed. Then the Tutte polynomial is defined by the recurrence relation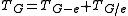 if
if  is neither a loop nor a bridge
is neither a loop nor a bridgewith base case
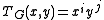 if
if  contains
contains  bridges and
bridges and  loops and no other edges.
loops and no other edges.Especially,
 if
if 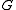 contains no edges.
contains no edges.The random cluster model from statistical mechanics provides yet another equivalent definition. The polynomial
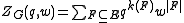
is equivalent to
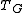 under the transformation
under the transformation .
.Properties
The Tutte polynomial factors into connected components: If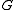 is the union of disjoint graphs
is the union of disjoint graphs 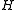
and
 then
then
If
 is planar and
is planar and 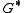 denotes its dual graph
denotes its dual graphDual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
then
Especially, the chromatic polynomial of a planar graph is the flow polynomial of its dual.
Examples
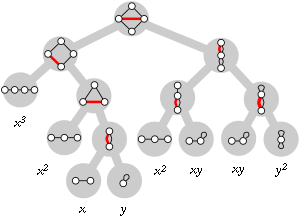
Isomorphic graphs have the same Tutte polynomial, but the opposite is not true. For example, the Tutte polynomial of every tree on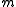 edges is
edges is  .
.Tutte polynomials are often given in tabular form by listing the coefficients
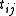 of
of 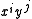 in row
in row 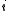 and column
and column 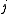 . For example, the Tutte polynomial of the Petersen graph
. For example, the Tutte polynomial of the Petersen graphPetersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
,
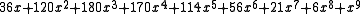
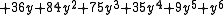

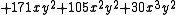


is given by the following table.
|114
|->
History
W. T. TutteW. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
’s interest in the deletion–contraction formula started in his undergraduate days at Trinity College, Cambridge
Trinity College, Cambridge
Trinity College is a constituent college of the University of Cambridge. Trinity has more members than any other college in Cambridge or Oxford, with around 700 undergraduates, 430 graduates, and over 170 Fellows...
, originally motivated by perfect rectangles and spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s. He often applied the formula in his research and “wondered if there were other interesting functions of graphs, invariant under isomorphism, with similar recursion formulae.” R. M. Foster
R. M. Foster
Ronald Martin Foster , was a Bell Labs mathematician whose work was of significance regarding electronic filters for use on telephone lines...
had already observed that the chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
is one such function, and Tutte began to discover more. His original terminology for graph invariants that satisfy the delection–contraction recursion was W-function (and V-function if multiplicative over component). Tutte writes, “Playing with my W-functions I obtained a two-variable polynomial from which either
the chromatic polynomial or the flow-polynomial could be obtained by setting one of the
variables equal to zero, and adjusting signs.” Tutte called this function the dichromate, as he saw it as a generalization of the chromatic polynomial to two variables, but it is usually referred to as the Tutte polynomial. In Tutte’s words, “This may be unfair to Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
who knew and used analogous coefficients without bothering to affix them to two variables.” There is “notable confusion” about the terms dichromate and dichromatic polynomial, introduced by Tutte in different papers and differ slightly.
The generalisation of the Tutte polynomial to matroids was first published by Crapo, though it appears already in Tutte’s thesis.
Independently of the work in algebraic graph theory
Algebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
, Potts began studying the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of certain models in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
in 1952. The work of Fortuin and Kasteleyn
Pieter Kasteleyn
Pieter Willem Kasteleyn was a Dutch physicist famous for his contributions to the field of Statistical Mechanics.-Biography:...
on the random cluster model, a generalisation of Potts model
Potts model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
, provided a unifying expression that showed the relation to the Tutte polynomial.
Specialisations
At various points and lines of the -plane, the Tutte polynomial evaluates to quantities that have been studied in their own right in diverse fields of mathematics and physics. Part of the appeal of the Tutte polynomial comes from the unifying framework it provides for analysing these quantities.
-plane, the Tutte polynomial evaluates to quantities that have been studied in their own right in diverse fields of mathematics and physics. Part of the appeal of the Tutte polynomial comes from the unifying framework it provides for analysing these quantities.Chromatic polynomial

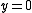 , the Tutte polynomial specialises to the chromatic polynomial,
, the Tutte polynomial specialises to the chromatic polynomial,
where
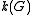 denote the number of connected components of
denote the number of connected components of 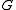
For integer
 the value of chromatic polynomial
the value of chromatic polynomial 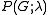 equals the number of vertex colourings of
equals the number of vertex colourings of 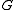 using a set of
using a set of 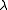 colours. It is clear that
colours. It is clear that  does not depend on the set of colours. What is less clear is that it is the evaluation at
does not depend on the set of colours. What is less clear is that it is the evaluation at  of a polynomial with integer coefficients. To see this, we observe:
of a polynomial with integer coefficients. To see this, we observe:
- If
 has
has  vertices and no edges, then
vertices and no edges, then 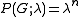 .
. - If
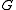 contains a loop (a single edge connecting a vertex to itself), then
contains a loop (a single edge connecting a vertex to itself), then  .
. - If
 is an edge which is not a loop, then
is an edge which is not a loop, then
The three conditions above enable us to calculate
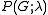 ,
,by applying a sequence of edge deletions and contractions; but they give no guarantee that a different sequence of deletions and contractions will lead to the same value. The guarantee comes from the fact that
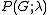 counts something, independently of the recurrence. In particular,
counts something, independently of the recurrence. In particular, 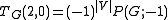 gives the number of acyclic orientations.
gives the number of acyclic orientations.Jones polynomial

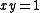 the Tutte polynomial specialises to the Jones polynomial of an alternating knot
the Tutte polynomial specialises to the Jones polynomial of an alternating knotAlternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
if
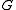 is planar.
is planar.Individual points
(2,1)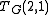 counts the number of forest
counts the number of forestTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s, i.e., the number of acyclic edge subsets.
(1,1)
-
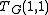 equals the number of spanning trees.
equals the number of spanning trees.
(1,2)
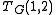 the Tutte polynomial counts the number of connected spanning subgraphs.
the Tutte polynomial counts the number of connected spanning subgraphs.(0,2)
 counts the number of strongly connected orientations
counts the number of strongly connected orientationsRobbins theorem
In graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs...
of G.
(3,3)
- If
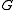 is the
is the 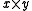 grid graph then
grid graph then 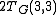 equals the number of ways to tile a rectangle of width
equals the number of ways to tile a rectangle of width 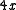 and height
and height  with T-tetrominoesTetrominoA tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino...
with T-tetrominoesTetrominoA tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino...
.
Potts and Ising models
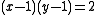 , the Tutte polynomial specialises to the partition function of the Ising model
, the Tutte polynomial specialises to the partition function of the Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
studied in statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
.
More generally, along the hyperbolae
 defined by
defined by 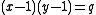 for any positive integer
for any positive integer  , the Tutte polynomial specialises to the partition function of the
, the Tutte polynomial specialises to the partition function of the 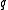 -state Potts model
-state Potts modelPotts model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
.
Various physical quantities analysed in the framework of the Potts model translate to specific parts of the
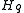 .
.| Potts model | Tutte polynomial |
|---|---|
| Ferromagnetism Ferromagnetism Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished... |
Positive branch of  |
| Antiferromagnetism Antiferromagnetism In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usuallyrelated to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism... |
Negative branch of 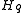 with with 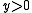 |
| High temperature | Asymptote of  to to 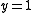 |
| Low temperature ferromagnetic | Positive branch of 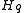 asymptotic to asymptotic to 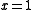 |
| Zero temperature antiferromagnetic | Graph 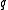 -colouring -colouringGraph coloring In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the... , i.e.,  |
Flow polynomial
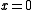 , the Tutte polynomial specialises to the flow polynomial studied in combinatorics. For a connected and undirected graph
, the Tutte polynomial specialises to the flow polynomial studied in combinatorics. For a connected and undirected graph  and integer
and integer 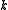 , a nowhere-zero
, a nowhere-zero 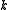 -flow is an assignment of “flow” values
-flow is an assignment of “flow” values  to the edges of an arbitrary orientation of
to the edges of an arbitrary orientation of 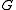 such that the total flow entering and leaving each vertex is congruent modulo
such that the total flow entering and leaving each vertex is congruent modulo 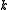 .
.The flow polynomial
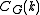 denotes the number of nowhere-zero
denotes the number of nowhere-zero 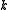 -flows. This value is intimately connected with the chromatic polynomial, in fact, if
-flows. This value is intimately connected with the chromatic polynomial, in fact, if  is a planar graph
is a planar graphPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, the chromatic polynomial of
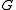 is equivalent to the flow polynomial of its dual graph
is equivalent to the flow polynomial of its dual graphDual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
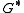 in the sense that
in the sense that
- Theorem (Tutte):
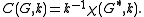
The connection to the Tutte polynomial is given by
Reliability polynomial
 , the Tutte polynomial specialises to the all-terminal reliability polynomial studied in network theory. For a connected graph
, the Tutte polynomial specialises to the all-terminal reliability polynomial studied in network theory. For a connected graph  remove every edge with probability
remove every edge with probability  ; this models a network subject to random edge failures. Then the reliability polynomial is a function
; this models a network subject to random edge failures. Then the reliability polynomial is a function  , a polynomial in
, a polynomial in 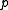 , that gives the probability that every pair of vertices in
, that gives the probability that every pair of vertices in  remains connected after the edges fail. The connection to the Tutte polynomial is given by
remains connected after the edges fail. The connection to the Tutte polynomial is given by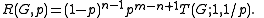
Dichromatic polynomial
Tutte also defined a closer 2-variable generalization of the chromatic polynomial, the dichromatic polynomial of a graph. This is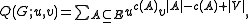
where
 is the number of connected components
is the number of connected componentsConnected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
of the spanning subgraph (V,A). This is related to the corank-nullity polynomial by
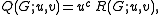
where c is the number of components of G. The dichromatic polynomial does not generalize to matroids because c is not a matroid property: different graphs with the same matroid can have different numbers of components.
Deletion–contraction
-
 (
( not a loop nor a bridge)
not a loop nor a bridge)
immediately yields a recursive algorithm for computing it: choose any such edge
 and repeatedly apply the formula until all edges are either loops or bridges; the resulting base cases at the bottom of the evaluation are easy to compute.
and repeatedly apply the formula until all edges are either loops or bridges; the resulting base cases at the bottom of the evaluation are easy to compute.Within a polynomial factor, the running time
 of this algorithm can be expressed in terms of the number of vertices
of this algorithm can be expressed in terms of the number of vertices  and the number of edges
and the number of edges 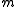 of the graph,
of the graph,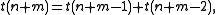
a recurrence relation that scales as the Fibonacci numbers with solution
 √
√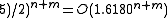 . The analysis can be improved to within a polynomial factor of the number
. The analysis can be improved to within a polynomial factor of the number  of spanning trees
of spanning treesSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of the input graph. For sparse graphs with
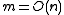 this running time is
this running time is 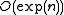 . For regular graphs of degree
. For regular graphs of degree 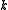 , the number of spanning trees can be bounded by
, the number of spanning trees can be bounded by
-
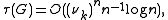 where
where 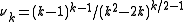
so the deletion–contraction algorithm runs within a polynomial factor of this bound. For example, for
 , the base of the exponent
, the base of the exponent  is around 4.4066.
is around 4.4066.In practice, graph isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
testing is used to avoid some recursive calls. This approach works well for graphs that are quite sparse and exhibit many symmetries; the performance of the algorithm depends on the heuristic used to pick the edge e.
Gaussian elimination
In some restricted instances, the Tutte polynomial can be computed in polynomial time, ultimately because Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
efficiently computes the matrix operations determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
. These algorithms are themselves important results from algebraic graph theory
Algebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
 equals the number
equals the number 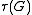 of spanning tree
of spanning treeSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s of a connected graph. This is
computable in polynomial time as the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
a maximal principal submatrix of the Laplacian matrix
Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
of
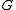 ,
,an early result in algebraic graph theory known as Kirchhoff’s Matrix–Tree theorem.
Likewise, the dimension of the bicycle space at
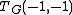 can be computed in polynomial time by Gaussian
can be computed in polynomial time by Gaussianelimination.
For planar graphs, the partition function of the Ising model, i.e., the Tutte polynomial at the hyperbola
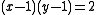 , can be expressed as a Pfaffian and computed efficiently via the FKT algorithm
, can be expressed as a Pfaffian and computed efficiently via the FKT algorithmFKT algorithm
The FKT algorithm, named after Fisher, Kasteleyn, and Temperley, counts the number of perfect matchings in a planar graph in polynomial time. This same task is #P-complete for general graphs. Counting the number of matchings, even for planar graphs, is also #P-complete...
. This idea was developed by Fisher
Michael Fisher
Michael Ellis Fisher is an English physicist, as well as chemist and mathematician, known for his many seminal contributions...
, Kasteleyn
Pieter Kasteleyn
Pieter Willem Kasteleyn was a Dutch physicist famous for his contributions to the field of Statistical Mechanics.-Biography:...
, and Temperley
Harold Neville Vazeille Temperley
Harold Neville Vazeille Temperley is a mathematical physicist working on "lattice gases". His father, Harold William Vazeille Temperley, was a distinguished British historian....
to compute for the number of dimer
Domino tiling
A domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge...
covers of a planar lattice model
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
.
Markov chain Monte Carlo
Using a Markov chain Monte CarloMarkov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
method, the Tutte polynomial can be arbitrarily well approximated along the positive branch of
 , equivalently, the partition function of the ferromagnetic Ising model. This exploits the close connection between the Ising model and the problem of counting matchings in a graph. The idea behind this celebrated result of Jerrum and Sinclair is to set up a Markov chain
, equivalently, the partition function of the ferromagnetic Ising model. This exploits the close connection between the Ising model and the problem of counting matchings in a graph. The idea behind this celebrated result of Jerrum and Sinclair is to set up a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
whose states are the matchings of the input graph. The transitions are defined by choosing edges at random and modifying the matching accordingly. The resulting Markov chain is rapidly mixing and leads to “sufficiently random” matchings, which can be used to recover the partition function using random sampling. The resulting algorithm is a fully polynomial-time randomized approximation scheme (fpras).
Computational complexity
Several computational problems are associated with the Tutte polynomial. The most straightforward one isInput
- A graph
Output
- The coefficients of
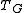
Especially, the output allows evaluating
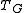 at
at  , equivalent to counting the number of 3-colourings of
, equivalent to counting the number of 3-colourings of  This latter question is #P-complete even restricted to the family of planar graph
This latter question is #P-complete even restricted to the family of planar graphPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, so the problem of computing the coefficients of the Tutte polynomial for a given graph is #P-hard even for planar graphs.
Much more attention has been given to the family of problems called Tutte
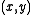 defined for every rational pair
defined for every rational pair 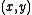 :
:Input
- A graph
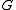
Output
- The value of

The hardness of these problems varies with the coordinates
 .
.Exact computation
If both and
and  are nonnegative integers, the problem Tutte
are nonnegative integers, the problem Tutte belongs to #P
belongs to #PSharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
. For general integer pairs, the Tutte polynomial contains negative terms, which places the problem in the complexity class GapP
GapP
GapP is a counting complexity class, consisting of all of the functions f such that there exists a polynomial-time non-deterministic Turing machine M where, for any input x, f is equal to the number of accepting paths of M minus the number of rejecting paths of M. GapP is exactly the closure of...
, the closure under subtraction of #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
. To accommodate rational coordinates
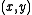 , one can define a rational analogue of #P
, one can define a rational analogue of #PSharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
.
The computational complexity of exactly computing Tutte
 is completely understood for
is completely understood for 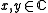 . The problem is #P-hard unless
. The problem is #P-hard unless 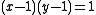 or
or 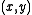 is one of the points (1, 1), (-1, -1), (0, -1), (-1, 0), (i, -i), (-i, i), (j, j2), (j2, j) where
is one of the points (1, 1), (-1, -1), (0, -1), (-1, 0), (i, -i), (-i, i), (j, j2), (j2, j) where 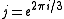 , in which cases it is computable in polynomial time. If the problem is restricted to the class of planar graphs, the points on the hyperbola defined by
, in which cases it is computable in polynomial time. If the problem is restricted to the class of planar graphs, the points on the hyperbola defined by  become polynomial-time computable, but all other points remain #P-hard. This result contains several notable special cases. For example, the problem of computing the partition function of the Ising model is #P-hard in general, even though celebrated algorithms of Onsager and Fisher solve it for planar lattices. Also, the Jones polynomial is #P-hard to compute. Finally, computing the number of four-colourings of a planar graph is #P-complete, even though the decision problem is trivial by the four color theorem
become polynomial-time computable, but all other points remain #P-hard. This result contains several notable special cases. For example, the problem of computing the partition function of the Ising model is #P-hard in general, even though celebrated algorithms of Onsager and Fisher solve it for planar lattices. Also, the Jones polynomial is #P-hard to compute. Finally, computing the number of four-colourings of a planar graph is #P-complete, even though the decision problem is trivial by the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. In contrast, it is easy to see that counting the number of three-colourings for planar graphs is #P-complete because the decision problem is known to be NP-complete.
Approximation
The question which points admit a good approximation algorithm has been very well studied.Apart from the points already in P, the only approximation algorithm known for Tutte
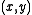 is Jerrum and Sinclair’s FPRAS, which works for points on the “Ising” hyperbola
is Jerrum and Sinclair’s FPRAS, which works for points on the “Ising” hyperbola 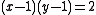 for y > 0. If the input graphs are restricted to dense instances, with degree
for y > 0. If the input graphs are restricted to dense instances, with degree  , there is an FPRAS if x ≥ 1, y ≥ 1.
, there is an FPRAS if x ≥ 1, y ≥ 1.Even though the situation is not as well understood as for exact computation, large areas of the plane are known to be hard to approximate.
External links
- PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
Chromatic polynomial - Steven R. Pagano: Matroids and Signed Graphs
- Sandra Kingan: Matroid theory. Lots of links.
- Code for computing Tutte, Chromatic and Flow Polynomials by Gary Haggard, David J. Pearce and Gordon Royle: http://www.ecs.vuw.ac.nz/~djp/tutte/