
Potts model
Encyclopedia
In statistical mechanics
, the Potts model, a generalization of the Ising model
, is a model of interacting spins
on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics. The strength of the Potts model is not so much that it models these physical systems well; it is rather that the one-dimensional case is exactly solvable, and that it has a rich mathematical formulation that has been studied extensively.
The model is named after Renfrey B. Potts who described the model near the end of his 1952 Ph.D. thesis. The model was related to the "planar Potts" or "clock model", which was suggested to him by his advisor Cyril Domb
. The Potts model is sometimes known as the Ashkin–Teller model (after Julius Ashkin and Edward Teller
), as they considered a four component version in 1943.
The Potts model is related to, and generalized by, several other models, including the XY model
, the Heisenberg model
and the N-vector model. The infinite-range Potts model is known as the Kac model. When the spins are taken to interact in a non-Abelian
manner, the model is related to the flux tube model, which is used to discuss confinement in quantum chromodynamics
. Generalizations of the Potts model have also been used to model grain growth
in metals and coarsening in foam
s. A further generalization of these methods by James Glazier and Francois Graner, known as the Cellular Potts model
has been used to simulate static and kinetic phenomena in foam and biological morphogenesis
.
; the lattice is usually taken to be a two-dimensional rectangular Euclidean
lattice, but is often generalized to other dimensions or other lattices. Domb originally suggested that the spin take one of q possible values, distributed uniformly about the circle
, at angles
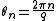 , where
, where 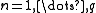
and that the interaction Hamiltonian
be given by
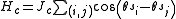
with the sum running over the nearest neighbor pairs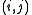 over all lattice sites. The site colors
over all lattice sites. The site colors 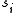 take on values, ranging from
take on values, ranging from  . Here,
. Here, 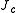 is a coupling constant, determining the interaction strength. This model is now known as the vector Potts model or the clock model. Potts provided a solution for two dimensions, for q=2,3 and 4. In the limit as q approaches infinity, this becomes the XY model
is a coupling constant, determining the interaction strength. This model is now known as the vector Potts model or the clock model. Potts provided a solution for two dimensions, for q=2,3 and 4. In the limit as q approaches infinity, this becomes the XY model
.
What is now known as the standard Potts model was suggested by Potts in the course of the solution above, and uses a simpler Hamiltonian, given by:
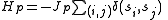
where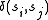 is the Kronecker delta, which equals one whenever
is the Kronecker delta, which equals one whenever 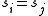 and zero otherwise.
and zero otherwise.
The q=2 standard Potts model is equivalent to the 2D Ising model
and the 2-state vector Potts model, with . The q=3 standard Potts model is equivalent to the three-state vector Potts model, with
. The q=3 standard Potts model is equivalent to the three-state vector Potts model, with 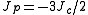 .
.
A common generalization is to introduce an external "magnetic field" term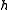 , and moving the parameters inside the sums and allowing them to vary across the model:
, and moving the parameters inside the sums and allowing them to vary across the model:
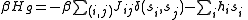
where the inverse temperature, k the Boltzmann constant and T the temperature
the inverse temperature, k the Boltzmann constant and T the temperature
. The summation may run over more distant neighbors on the lattice, or may in fact be an infinite-range force.
Different papers may adopt slightly different conventions, which can alter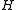 and the associated partition function
and the associated partition function
by additive or multiplicative constants.
s. For example, two dimensional lattices with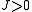 exhibit a first order transition if
exhibit a first order transition if  . When
. When 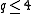 a continuous transition is observed, as in the Ising model where
a continuous transition is observed, as in the Ising model where 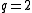 . Further use is found through the model's relation to percolation problems and the Tutte and chromatic polynomials found in combinatorics.
. Further use is found through the model's relation to percolation problems and the Tutte and chromatic polynomials found in combinatorics.
The model has a close relation to the Fortuin-Kasteleyn
random cluster model, another model in statistical mechanics. Understanding this relationship has helped develop efficient Markov chain Monte Carlo
methods for numerical exploration of the model at small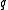 .
.
, and thus gains access to all of the mathematical techniques associated with this formalism. In particular, it can be solved exactly using the techniques of transfer operator
s. (However, Ernst Ising
used combinatorial methods to solve the Ising model
, which is the "ancestor" of the Potts model, in his 1925 PhD thesis). This section develops the mathematical formalism, based on measure theory, behind this solution.
While the example below is developed for the one-dimensional case, many of the arguments, and almost all of the notation, generalizes easily to any number of dimensions. Some of the formalism is also broad enough to handle related models, such as the XY model
, the Heisenberg model
and the N-vector model.
 be a finite set of symbols, and let
be a finite set of symbols, and let
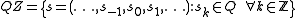
be the set of all bi-infinite strings of values from the set Q. This set is called a full shift. For defining the Potts model, either this whole space, or a certain subset of it, a subshift of finite type
, may be used. Shifts get this name because there exists a natural operator on this space, the shift operator
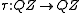 , acting as
, acting as

This set has a natural product topology
; the base
for this topology are the cylinder set
s
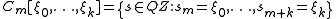
that is, the set of all possible strings where k+1 spins match up exactly to a given, specific set of values . Explicit representations for the cylinder sets can be gotten by noting that the string of values corresponds to a q-adic number
. Explicit representations for the cylinder sets can be gotten by noting that the string of values corresponds to a q-adic number
, and thus, intuitively, the product topology resembles that of the real number
line.
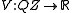 on this topology. Any continuous function will do; for example
on this topology. Any continuous function will do; for example
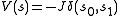
will be seen to describe the interaction between nearest neighbors. Of course, different functions give different interactions; so a function of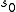 ,
, 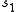 and
and 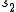 will describe a next-nearest neighbor interaction. A function V gives interaction energy between a set of spins; it is not the Hamiltonian, but is used to build it. The argument to the function V is an element
will describe a next-nearest neighbor interaction. A function V gives interaction energy between a set of spins; it is not the Hamiltonian, but is used to build it. The argument to the function V is an element  , that is, an infinite string of spins. In the above example, the function V just picked out two spins out of the infinite string: the values
, that is, an infinite string of spins. In the above example, the function V just picked out two spins out of the infinite string: the values 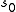 and
and  . In general, the function V may depend on some or all of the spins; currently, only those that depend on a finite number are exactly solvable.
. In general, the function V may depend on some or all of the spins; currently, only those that depend on a finite number are exactly solvable.
Define the function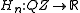 as
as
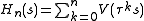
This function can be seen to consist of two parts: the self-energy of a configuration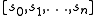 of spins, plus the interaction energy of this set and all the other spins in the lattice. The
of spins, plus the interaction energy of this set and all the other spins in the lattice. The 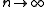 limit of this function is the Hamiltonian of the system; for finite n, these are sometimes called the finite state Hamiltonians.
limit of this function is the Hamiltonian of the system; for finite n, these are sometimes called the finite state Hamiltonians.
is given by

with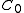 being the cylinder sets defined above. Here, β=1/kT, where k is Boltzmann's constant, and T is the temperature
being the cylinder sets defined above. Here, β=1/kT, where k is Boltzmann's constant, and T is the temperature
. It is very common in mathematical treatments to set β=1, as it is easily regained by rescaling the interaction energy. This partition function is written as a function of the interaction V to emphasize that it is only a function of the interaction, and not of any specific configuration of spins. The partition function, together with the Hamiltonian, are used to define a measure
on the Borel σ-algebra in the following way: The measure of a cylinder set, i.e. an element of the base, is given by

One can then extend by countable additivity to the full σ-algebra. This measure is a probability measure
; it gives the likelihood of a given configuration occurring in the configuration space
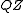 . By endowing the configuration space with a probability measure built from a Hamiltonian in this way, the configuration space turns into a canonical ensemble
. By endowing the configuration space with a probability measure built from a Hamiltonian in this way, the configuration space turns into a canonical ensemble
.
Most thermodynamic properties can be expressed directly in terms of the partition function. Thus, for example, the Helmholtz free energy
is given by
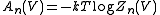
Another important related quantity is the topological pressure, defined as
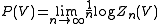
which will show up as the logarithm of the leading eigenvalue of the transfer operator
of the solution.
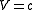 and
and 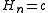 (with
(with  constant and independent of any spin configuration). The partition function becomes
constant and independent of any spin configuration). The partition function becomes
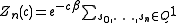
If all states are allowed, that is, the underlying set of states is given by a full shift, then the sum may be trivially evaluated as
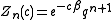
If neighboring spins are only allowed in certain specific configurations, then the state space is given by a subshift of finite type
. The partition function may then be written as
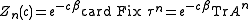
where card is the cardinality or count of a set, and Fix is the set of fixed points
of the iterated shift function:
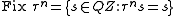
The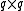 matrix
matrix 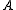 is the adjacency matrix
is the adjacency matrix
specifying which neighboring spin values are allowed.
, where the spin can only take on one of two values, and only nearest neighbor spins interact. The interaction potential is given by
and only nearest neighbor spins interact. The interaction potential is given by
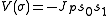
This potential can be captured in a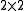 matrix with matrix elements
matrix with matrix elements
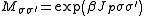
with the index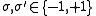 . The partition function is then given by
. The partition function is then given by
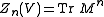
The general solution for an arbitrary number of spins, and an arbitrary finite-range interaction, is given by the same general form. In this case, the precise expression for the matrix M is a bit more complex.
The goal of solving a model such as the Potts model is to give the an exact closed-form expression
for the partition function (which we've done) and an expression for the Gibbs state
s or equilibrium states in the limit of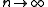 , the thermodynamic limit
, the thermodynamic limit
.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Potts model, a generalization of the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, is a model of interacting spins
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics. The strength of the Potts model is not so much that it models these physical systems well; it is rather that the one-dimensional case is exactly solvable, and that it has a rich mathematical formulation that has been studied extensively.
The model is named after Renfrey B. Potts who described the model near the end of his 1952 Ph.D. thesis. The model was related to the "planar Potts" or "clock model", which was suggested to him by his advisor Cyril Domb
Cyril Domb
Cyril Domb is a physicist best known for his lecturing and writing on the theory of phase transitions and critical phenomena of fluids. He is also known in the Orthodox Jewish world for his writings on Science and Judaism...
. The Potts model is sometimes known as the Ashkin–Teller model (after Julius Ashkin and Edward Teller
Edward Teller
Edward Teller was a Hungarian-American theoretical physicist, known colloquially as "the father of the hydrogen bomb," even though he did not care for the title. Teller made numerous contributions to nuclear and molecular physics, spectroscopy , and surface physics...
), as they considered a four component version in 1943.
The Potts model is related to, and generalized by, several other models, including the XY model
XY model
The classical XY model is a model of statistical mechanics. It is the special case of the n-vector model for n=2.-Definition:...
, the Heisenberg model
Heisenberg model
The Heisenberg model can refer to two models in statistical mechanics:*Heisenberg model , a classical nearest neighbour spin model*Heisenberg model , a model where the spins are treated quantum mechanically using Pauli matrices....
and the N-vector model. The infinite-range Potts model is known as the Kac model. When the spins are taken to interact in a non-Abelian
Non-abelian
In theoretical physics, a non-abelian gauge transformation means a gauge transformation taking values in some group G, the elements of which do not obey the commutative law when they are multiplied. The original choice of G in the physics of electromagnetism was U, which is commutative.For a...
manner, the model is related to the flux tube model, which is used to discuss confinement in quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. Generalizations of the Potts model have also been used to model grain growth
Grain growth
Grain growth is the increase in size of grains in a material at high temperature. This occurs when recovery and recrystallisation are complete and further reduction in the internal energy can only be achieved by reducing the total area of grain boundary...
in metals and coarsening in foam
Foam
-Definition:A foam is a substance that is formed by trapping gas in a liquid or solid in a divided form, i.e. by forming gas regions inside liquid regions, leading to different kinds of dispersed media...
s. A further generalization of these methods by James Glazier and Francois Graner, known as the Cellular Potts model
Cellular Potts model
The cellular Potts model is a lattice-based computational modeling method to simulate the collective behavior of cellular structures. Other names for the CPM are extended large-q Potts model and Glazier and Graner model...
has been used to simulate static and kinetic phenomena in foam and biological morphogenesis
Morphogenesis
Morphogenesis , is the biological process that causes an organism to develop its shape...
.
Physical description
The Potts model consists of spins that are placed on a latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
; the lattice is usually taken to be a two-dimensional rectangular Euclidean
Euclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
lattice, but is often generalized to other dimensions or other lattices. Domb originally suggested that the spin take one of q possible values, distributed uniformly about the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, at angles
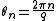 , where
, where 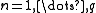
and that the interaction Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
be given by
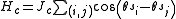
with the sum running over the nearest neighbor pairs
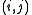 over all lattice sites. The site colors
over all lattice sites. The site colors 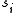 take on values, ranging from
take on values, ranging from  . Here,
. Here, 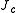 is a coupling constant, determining the interaction strength. This model is now known as the vector Potts model or the clock model. Potts provided a solution for two dimensions, for q=2,3 and 4. In the limit as q approaches infinity, this becomes the XY model
is a coupling constant, determining the interaction strength. This model is now known as the vector Potts model or the clock model. Potts provided a solution for two dimensions, for q=2,3 and 4. In the limit as q approaches infinity, this becomes the XY modelXY model
The classical XY model is a model of statistical mechanics. It is the special case of the n-vector model for n=2.-Definition:...
.
What is now known as the standard Potts model was suggested by Potts in the course of the solution above, and uses a simpler Hamiltonian, given by:
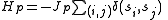
where
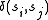 is the Kronecker delta, which equals one whenever
is the Kronecker delta, which equals one whenever 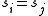 and zero otherwise.
and zero otherwise.The q=2 standard Potts model is equivalent to the 2D Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
and the 2-state vector Potts model, with
 . The q=3 standard Potts model is equivalent to the three-state vector Potts model, with
. The q=3 standard Potts model is equivalent to the three-state vector Potts model, with 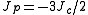 .
.A common generalization is to introduce an external "magnetic field" term
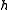 , and moving the parameters inside the sums and allowing them to vary across the model:
, and moving the parameters inside the sums and allowing them to vary across the model: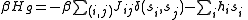
where
 the inverse temperature, k the Boltzmann constant and T the temperature
the inverse temperature, k the Boltzmann constant and T the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. The summation may run over more distant neighbors on the lattice, or may in fact be an infinite-range force.
Different papers may adopt slightly different conventions, which can alter
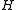 and the associated partition function
and the associated partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
by additive or multiplicative constants.
Discussion
Despite its simplicity as a model of a physical system, the Potts model is useful as a model system for the study of phase transitionPhase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s. For example, two dimensional lattices with
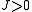 exhibit a first order transition if
exhibit a first order transition if  . When
. When 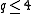 a continuous transition is observed, as in the Ising model where
a continuous transition is observed, as in the Ising model where 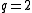 . Further use is found through the model's relation to percolation problems and the Tutte and chromatic polynomials found in combinatorics.
. Further use is found through the model's relation to percolation problems and the Tutte and chromatic polynomials found in combinatorics.The model has a close relation to the Fortuin-Kasteleyn
Pieter Kasteleyn
Pieter Willem Kasteleyn was a Dutch physicist famous for his contributions to the field of Statistical Mechanics.-Biography:...
random cluster model, another model in statistical mechanics. Understanding this relationship has helped develop efficient Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methods for numerical exploration of the model at small
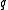 .
.Measure theoretic description
The one dimensional Potts model may be expressed in terms of a subshift of finite typeSubshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
, and thus gains access to all of the mathematical techniques associated with this formalism. In particular, it can be solved exactly using the techniques of transfer operator
Transfer operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
s. (However, Ernst Ising
Ernst Ising
Ernst Ising was a German physicist, who is best remembered for the development of the Ising model. He was a professor of physics at Bradley University until his retirement in 1976.-Life:Ernst Ising was born in Cologne in 1900...
used combinatorial methods to solve the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, which is the "ancestor" of the Potts model, in his 1925 PhD thesis). This section develops the mathematical formalism, based on measure theory, behind this solution.
While the example below is developed for the one-dimensional case, many of the arguments, and almost all of the notation, generalizes easily to any number of dimensions. Some of the formalism is also broad enough to handle related models, such as the XY model
XY model
The classical XY model is a model of statistical mechanics. It is the special case of the n-vector model for n=2.-Definition:...
, the Heisenberg model
Heisenberg model
The Heisenberg model can refer to two models in statistical mechanics:*Heisenberg model , a classical nearest neighbour spin model*Heisenberg model , a model where the spins are treated quantum mechanically using Pauli matrices....
and the N-vector model.
Topology of the space of states
Let be a finite set of symbols, and let
be a finite set of symbols, and let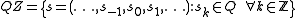
be the set of all bi-infinite strings of values from the set Q. This set is called a full shift. For defining the Potts model, either this whole space, or a certain subset of it, a subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
, may be used. Shifts get this name because there exists a natural operator on this space, the shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
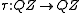 , acting as
, acting as
This set has a natural product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
; the base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for this topology are the cylinder set
Cylinder set
In mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s
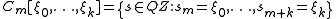
that is, the set of all possible strings where k+1 spins match up exactly to a given, specific set of values
 . Explicit representations for the cylinder sets can be gotten by noting that the string of values corresponds to a q-adic number
. Explicit representations for the cylinder sets can be gotten by noting that the string of values corresponds to a q-adic numberP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
, and thus, intuitively, the product topology resembles that of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
line.
Interaction energy
The interaction between the spins is then given by a continuous function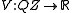 on this topology. Any continuous function will do; for example
on this topology. Any continuous function will do; for example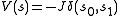
will be seen to describe the interaction between nearest neighbors. Of course, different functions give different interactions; so a function of
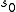 ,
, 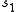 and
and 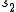 will describe a next-nearest neighbor interaction. A function V gives interaction energy between a set of spins; it is not the Hamiltonian, but is used to build it. The argument to the function V is an element
will describe a next-nearest neighbor interaction. A function V gives interaction energy between a set of spins; it is not the Hamiltonian, but is used to build it. The argument to the function V is an element  , that is, an infinite string of spins. In the above example, the function V just picked out two spins out of the infinite string: the values
, that is, an infinite string of spins. In the above example, the function V just picked out two spins out of the infinite string: the values 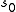 and
and  . In general, the function V may depend on some or all of the spins; currently, only those that depend on a finite number are exactly solvable.
. In general, the function V may depend on some or all of the spins; currently, only those that depend on a finite number are exactly solvable.Define the function
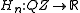 as
as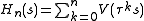
This function can be seen to consist of two parts: the self-energy of a configuration
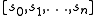 of spins, plus the interaction energy of this set and all the other spins in the lattice. The
of spins, plus the interaction energy of this set and all the other spins in the lattice. The 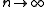 limit of this function is the Hamiltonian of the system; for finite n, these are sometimes called the finite state Hamiltonians.
limit of this function is the Hamiltonian of the system; for finite n, these are sometimes called the finite state Hamiltonians.Partition function and measure
The corresponding finite-state partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is given by

with
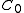 being the cylinder sets defined above. Here, β=1/kT, where k is Boltzmann's constant, and T is the temperature
being the cylinder sets defined above. Here, β=1/kT, where k is Boltzmann's constant, and T is the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. It is very common in mathematical treatments to set β=1, as it is easily regained by rescaling the interaction energy. This partition function is written as a function of the interaction V to emphasize that it is only a function of the interaction, and not of any specific configuration of spins. The partition function, together with the Hamiltonian, are used to define a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the Borel σ-algebra in the following way: The measure of a cylinder set, i.e. an element of the base, is given by

One can then extend by countable additivity to the full σ-algebra. This measure is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
; it gives the likelihood of a given configuration occurring in the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
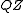 . By endowing the configuration space with a probability measure built from a Hamiltonian in this way, the configuration space turns into a canonical ensemble
. By endowing the configuration space with a probability measure built from a Hamiltonian in this way, the configuration space turns into a canonical ensembleCanonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
.
Most thermodynamic properties can be expressed directly in terms of the partition function. Thus, for example, the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
is given by
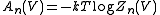
Another important related quantity is the topological pressure, defined as
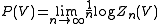
which will show up as the logarithm of the leading eigenvalue of the transfer operator
Transfer operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
of the solution.
Free field solution
The simplest model is the model where there is no interaction at all, and so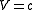 and
and 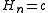 (with
(with  constant and independent of any spin configuration). The partition function becomes
constant and independent of any spin configuration). The partition function becomes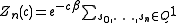
If all states are allowed, that is, the underlying set of states is given by a full shift, then the sum may be trivially evaluated as
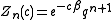
If neighboring spins are only allowed in certain specific configurations, then the state space is given by a subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
. The partition function may then be written as
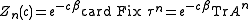
where card is the cardinality or count of a set, and Fix is the set of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the iterated shift function:
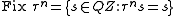
The
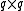 matrix
matrix 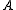 is the adjacency matrix
is the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
specifying which neighboring spin values are allowed.
Interacting model
The simplest case of the interacting model is the Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, where the spin can only take on one of two values,
 and only nearest neighbor spins interact. The interaction potential is given by
and only nearest neighbor spins interact. The interaction potential is given by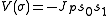
This potential can be captured in a
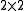 matrix with matrix elements
matrix with matrix elements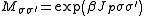
with the index
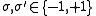 . The partition function is then given by
. The partition function is then given by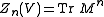
The general solution for an arbitrary number of spins, and an arbitrary finite-range interaction, is given by the same general form. In this case, the precise expression for the matrix M is a bit more complex.
The goal of solving a model such as the Potts model is to give the an exact closed-form expression
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
for the partition function (which we've done) and an expression for the Gibbs state
Gibbs state
In probability theory and statistical mechanics, a Gibbs state is an equilibrium probability distribution which remains invariant under future evolution of the system...
s or equilibrium states in the limit of
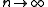 , the thermodynamic limit
, the thermodynamic limitThermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
.

