Robbins theorem
Encyclopedia
In graph theory
, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs
. That is, it is possible to choose a direction for each edge of an undirected graph , turning into a directed graph
that has a path from every vertex to every other vertex, if and only if is connected and has no bridge
.
Subsequently to the work of Robbins, a series of papers by Roberts and Xu modeled more carefully the problem of turning a grid of two-way city streets into one-way streets, and examined the effect of this conversion on the distances between pairs of points within the grid. As they showed, the traditional one-way layout in which parallel streets alternate in direction is not optimal in keeping the pairwise distances as small as possible. However, the improved orientations that they found include points where the traffic from two one-way blocks meets itself head-on, which may be viewed as a flaw in their solutions.
, a tool introduced by Robbins for this task.
If a graph has a bridge, then it cannot be strongly orientable, for no matter which orientation is chosen for the bridge there will be no path from one of the two endpoints of the bridge to the other.
In the other direction, it is necessary to show that every connected bridgeless graph can be strongly oriented. As Robbins proved, every such graph has a partition into a sequence of subgraphs called "ears", in which the first subgraph in the sequence is a cycle and each subsequent subgraph is a path, with the two path endpoints both belonging to earlier ears in the sequence. Orienting the edges within each ear so that it forms a directed cycle or a directed path leads to a strongly connected orientation of the overall graph.
that directs edges one at a time while preserving the existence of paths between every pair of vertices; it is impossible for such an algorithm to get stuck in a situation in which no additional orientation decisions can be made.
If an undirected graph has an Euler tour, an Eulerian orientation of the graph (an orientation for which every vertex has indegree equal to its outdegree) may be found by orienting the edges consistently around the tour. These orientations are automatically strong orientations.
A theorem of states that every undirected graph has a well-balanced orientation. This is an orientation with the property that, for every pair of vertices and in , the number of directed paths from to in the resulting directed graph is at least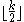
, where is the maximum number of paths in a set of edge-disjoint undirected paths from to . Nash-Williams' orientations also have the property that they are as close as possible to being Eulerian orientations: at each vertex, the indegree and the outdegree are within one of each other. The existence of well-balanced orientations, together with Menger's theorem
, immediately implies Robbins' theorem: by Menger's theorem, a 2-edge-connected graph has at least two edge-disjoint paths between every pair of vertices, from which it follows that any well-balanced orientation must be strongly connected. More generally this result implies that every -edge-connected undirected graph can be oriented to form a -edge-connected directed graph.
A totally cyclic orientation of a graph is an orientation in which each edge belongs to a directed cycle. For connected graphs, this is the same thing as a strong orientation, but totally cyclic orientations may also be defined for disconnected graphs, and are the orientations in which each connected component of becomes strongly connected. Robbins' theorem can be restarted as saying that a graph has a totally cyclic orientation if and only if it does not have a bridge. Totally cyclic orientations are dual to acyclic orientations (orientations that turn into a directed acyclic graph
) in the sense that, if is a planar graph
, and orientations of are transferred to orientations of the planar dual graph of by turning each edge 90 degrees clockwise, then a totally acyclic orientation of corresponds in this way to an acyclic orientation of the dual graph and vice versa. The number of different totally cyclic orientations of any graph is where is the Tutte polynomial
of the graph, and dually the number of acyclic orientations is . As a consequence, Robbins' theorem implies that the Tutte polynomial has a root at the point if and only if the graph has a bridge.
If is a 3-edge-connected graph, and and are any two different strong orientations of , then it is possible to transform into by changing the orientation of a single edge at a time, at each step preserving the property that the orientation is strong. Therefore, the flip graph whose vertices correspond to the strong orientations of , and whose edges correspond to pairs of strong orientations that differ in the direction of a single edge, forms a partial cube
.
If an undirected graph with bridges is given, together with a list of ordered pairs of vertices that must be connected by directed paths, it is possible in polynomial time to find an orientation of that connects all the given pairs, if such an orientation exists. However, the same problem is NP-complete
when the input may be a mixed graph.
It is #P-complete to count the number of strong orientations of a given graph , even when is planar and bipartite
. However, for dense graph
s (more specifically, graphs in which each vertex has a linear number of neighbors), the number of strong orientations may be estimated by a fully polynomial-time randomized approximation scheme. The problem of counting strong orientations may also be solved exactly, in polynomial time, for graphs of bounded treewidth.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
. That is, it is possible to choose a direction for each edge of an undirected graph , turning into a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
that has a path from every vertex to every other vertex, if and only if is connected and has no bridge
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
.
Application to traffic control
Robbins introduces the problem of strong orientation with a story about a town, whose streets and intersections are represented by the given graph . According to Robbins' story, the people of the town want to be able to repair any segment of road during the weekdays, while still allowing any part of the town to be reached from any other part using the remaining roads as two-way streets. On the weekends, all roads are open, but because of heavy traffic volume, they wish to convert all roads to one-way streets and again allow any part of town to be reached from any other part. Robbins' theorem states that a system of roads is suitable for weekday repairs if and only if it is suitable for conversion to a one-way system on weekends. For this reason, his result is sometimes known as the one-way street theorem.Subsequently to the work of Robbins, a series of papers by Roberts and Xu modeled more carefully the problem of turning a grid of two-way city streets into one-way streets, and examined the effect of this conversion on the distances between pairs of points within the grid. As they showed, the traditional one-way layout in which parallel streets alternate in direction is not optimal in keeping the pairwise distances as small as possible. However, the improved orientations that they found include points where the traffic from two one-way blocks meets itself head-on, which may be viewed as a flaw in their solutions.
Orientable graphs
Robbins' characterization of the graphs with strong orientations may be proven using ear decompositionEar decomposition
In graph theory, an ear of an undirected graph G is a path P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree two in P...
, a tool introduced by Robbins for this task.
If a graph has a bridge, then it cannot be strongly orientable, for no matter which orientation is chosen for the bridge there will be no path from one of the two endpoints of the bridge to the other.
In the other direction, it is necessary to show that every connected bridgeless graph can be strongly oriented. As Robbins proved, every such graph has a partition into a sequence of subgraphs called "ears", in which the first subgraph in the sequence is a cycle and each subsequent subgraph is a path, with the two path endpoints both belonging to earlier ears in the sequence. Orienting the edges within each ear so that it forms a directed cycle or a directed path leads to a strongly connected orientation of the overall graph.
Related results
An extension of Robbins' theorem to mixed graphs by shows that, if is a graph in which some edges may be directed and others undirected, and contains a path respecting the edge orientations from every vertex to every other vertex, then any undirected edge of that is not a bridge may be made directed without changing the connectivity of . In particular, a bridgeless undirected graph may be made into a strongly connected directed graph by a greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
that directs edges one at a time while preserving the existence of paths between every pair of vertices; it is impossible for such an algorithm to get stuck in a situation in which no additional orientation decisions can be made.
If an undirected graph has an Euler tour, an Eulerian orientation of the graph (an orientation for which every vertex has indegree equal to its outdegree) may be found by orienting the edges consistently around the tour. These orientations are automatically strong orientations.
A theorem of states that every undirected graph has a well-balanced orientation. This is an orientation with the property that, for every pair of vertices and in , the number of directed paths from to in the resulting directed graph is at least
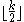, where is the maximum number of paths in a set of edge-disjoint undirected paths from to . Nash-Williams' orientations also have the property that they are as close as possible to being Eulerian orientations: at each vertex, the indegree and the outdegree are within one of each other. The existence of well-balanced orientations, together with Menger's theoremMenger's theorem
In the mathematical discipline of graph theory and related areas, Menger's theorem is a basic result about connectivity in finite undirected graphs. It was proved for edge-connectivity and vertex-connectivity by Karl Menger in 1927...
, immediately implies Robbins' theorem: by Menger's theorem, a 2-edge-connected graph has at least two edge-disjoint paths between every pair of vertices, from which it follows that any well-balanced orientation must be strongly connected. More generally this result implies that every -edge-connected undirected graph can be oriented to form a -edge-connected directed graph.
A totally cyclic orientation of a graph is an orientation in which each edge belongs to a directed cycle. For connected graphs, this is the same thing as a strong orientation, but totally cyclic orientations may also be defined for disconnected graphs, and are the orientations in which each connected component of becomes strongly connected. Robbins' theorem can be restarted as saying that a graph has a totally cyclic orientation if and only if it does not have a bridge. Totally cyclic orientations are dual to acyclic orientations (orientations that turn into a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
) in the sense that, if is a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, and orientations of are transferred to orientations of the planar dual graph of by turning each edge 90 degrees clockwise, then a totally acyclic orientation of corresponds in this way to an acyclic orientation of the dual graph and vice versa. The number of different totally cyclic orientations of any graph is where is the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
of the graph, and dually the number of acyclic orientations is . As a consequence, Robbins' theorem implies that the Tutte polynomial has a root at the point if and only if the graph has a bridge.
If is a 3-edge-connected graph, and and are any two different strong orientations of , then it is possible to transform into by changing the orientation of a single edge at a time, at each step preserving the property that the orientation is strong. Therefore, the flip graph whose vertices correspond to the strong orientations of , and whose edges correspond to pairs of strong orientations that differ in the direction of a single edge, forms a partial cube
Partial cube
In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...
.
Algorithms and complexity
A strong orientation of a given bridgeless undirected graph may be found in linear time by performing a depth first search of the graph, orienting all edges in the depth first search tree away from the tree root, and orienting all the remaining edges (which must necessarily connect an ancestor and a descendant in the depth first search tree) from the descendant to the ancestor. Although this algorithm is not suitable for parallel computers, due to the difficulty of performing depth first search on them, alternative algorithms are available that solve the problem efficiently in the parallel model. Parallel algorithms are also known for finding strongly connected orientations of mixed graphs.If an undirected graph with bridges is given, together with a list of ordered pairs of vertices that must be connected by directed paths, it is possible in polynomial time to find an orientation of that connects all the given pairs, if such an orientation exists. However, the same problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
when the input may be a mixed graph.
It is #P-complete to count the number of strong orientations of a given graph , even when is planar and bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. However, for dense graph
Dense graph
In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...
s (more specifically, graphs in which each vertex has a linear number of neighbors), the number of strong orientations may be estimated by a fully polynomial-time randomized approximation scheme. The problem of counting strong orientations may also be solved exactly, in polynomial time, for graphs of bounded treewidth.