Pfaffian
Encyclopedia
In mathematics
, the determinant
of a skew-symmetric matrix
can always be written as the square of a polynomial
in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff
. The Pfaffian is nonvanishing only for 2n × 2n skew-symmetric matrices, in which case it is a polynomial of degree n.
Explicitly, for a skew-symmetric matrix A,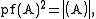
which was first proved by Thomas Muir
in 1882 .
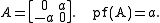
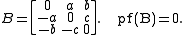
(3 x 3 is odd, so Pfaffian of B is 0)
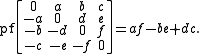
The Pfaffian of a 2n × 2n skew-symmetric tridiagonal matrix is given as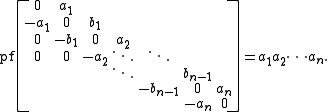
which contains the important case of a 2n × 2n skew-symmetric matrix with 2 × 2 blocks on the
diagonal: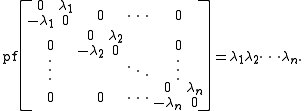
(Note that any skew-symmetric matrix can be reduced to this form, see Spectral theory of a skew-symmetric matrix)
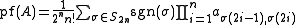
where S2n is the symmetric group
and sgn(σ) is the signature of σ.
One can make use of the skew-symmetry of A to avoid summing over all possible permutation
s. Let Π be the set of all partition
s of {1, 2, …, 2n} into pairs without regard to order. There are (2n − 1)!! such partitions. An element α ∈ Π can be written as
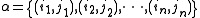
with ik < jk and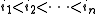
. Let
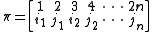
be the corresponding permutation. Given a partition α as above, define
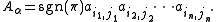
The Pfaffian of A is then given by
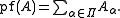
The Pfaffian of a n×n skew-symmetric matrix for n odd is defined to be zero, as the determinant of an odd skew-symmetric matrix is zero, since for a skew-symmetric matrix,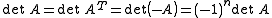
, and for n odd, this implies 
.
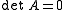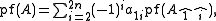
where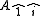
denotes the matrix A with both the first and i-th rows and columns removed.
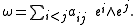
where {e1, e2, …, e2n} is the standard basis of R2n. The Pfaffian is then defined by the equation
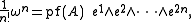
here ωn denotes the wedge product of n copies of ω with itself.
.
.
.
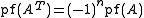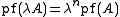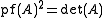For an arbitrary 2n × 2n matrix B,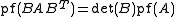
.
For a block-diagonal matrix
For an arbitrary n × n matrix M:
.
If A depends on some variable xi, then the gradient of Pfaffian is given by
,
and the Hessian of Pfaffian is given by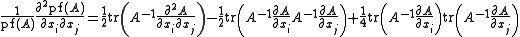
.
(Those properties can be derived from the identity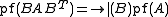
)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
can always be written as the square of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff
Johann Friedrich Pfaff
Johann Friedrich Pfaff was a German mathematician. He was described as one of Germany's most eminent mathematicians during the 19th century...
. The Pfaffian is nonvanishing only for 2n × 2n skew-symmetric matrices, in which case it is a polynomial of degree n.
Explicitly, for a skew-symmetric matrix A,
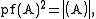
which was first proved by Thomas Muir
Thomas Muir (mathematician)
Sir Thomas Muir FRS was a Scottish mathematician, remembered as an authority on determinants. He was born in Stonebyres in South Lanarkshire, and brought up in the small town of Biggar. At the University of Glasgow he changed his studies from classics to mathematics after advice from the future...
in 1882 .
Examples
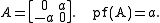
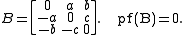
(3 x 3 is odd, so Pfaffian of B is 0)
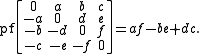
The Pfaffian of a 2n × 2n skew-symmetric tridiagonal matrix is given as
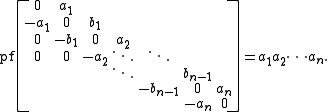
which contains the important case of a 2n × 2n skew-symmetric matrix with 2 × 2 blocks on the
diagonal:
(Note that any skew-symmetric matrix can be reduced to this form, see Spectral theory of a skew-symmetric matrix)
Formal definition
Let A = {ai,j} be a 2n × 2n skew-symmetric matrix. The Pfaffian of A is defined by the equation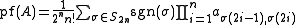where S2n is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and sgn(σ) is the signature of σ.
One can make use of the skew-symmetry of A to avoid summing over all possible permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s. Let Π be the set of all partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
s of {1, 2, …, 2n} into pairs without regard to order. There are (2n − 1)!! such partitions. An element α ∈ Π can be written as
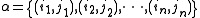
with ik < jk and
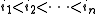. Let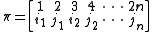be the corresponding permutation. Given a partition α as above, define
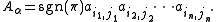
The Pfaffian of A is then given by
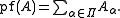
The Pfaffian of a n×n skew-symmetric matrix for n odd is defined to be zero, as the determinant of an odd skew-symmetric matrix is zero, since for a skew-symmetric matrix,
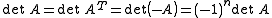, and for n odd, this implies 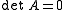.Recursive definition
By convention, the Pfaffian of the 0×0 matrix is equal to one. The Pfaffian of a skew-symmetric 2n×2n matrix A with n>0 can be computed recursively as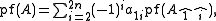where
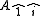denotes the matrix A with both the first and i-th rows and columns removed.Alternative definitions
- One can associate to any skew-symmetric 2n×2n matrix A ={aij} a bivectorExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
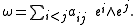
where {e1, e2, …, e2n} is the standard basis of R2n. The Pfaffian is then defined by the equation
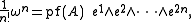
here ωn denotes the wedge product of n copies of ω with itself.
Identities
For a 2n × 2n skew-symmetric matrix A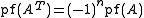..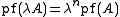.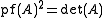For an arbitrary 2n × 2n matrix B,
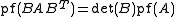.For a block-diagonal matrix
-
.
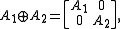
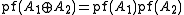For an arbitrary n × n matrix M:
.If A depends on some variable xi, then the gradient of Pfaffian is given by
,and the Hessian of Pfaffian is given by
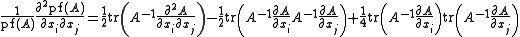.Properties
Pfaffians have the following properties similar to that of determinants- Multiplication of a row and a column by a constant is equivalent to multiplication of Pfaffian by the same constant.
- Simultaneous interchange of two different rows and corresponding columns changes the sign of Pfaffian.
- A multiple of a row and corresponding column added to another row and corresponding column does not change the value of Pfaffian.
(Those properties can be derived from the identity
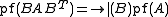)Applications
- The Pfaffian is an invariant polynomialInvariant polynomialIn mathematics, an invariant polynomial is a polynomial P that is invariant under a group \Gamma acting on a vector space V. Therefore P is a \Gamma-invariant polynomial ifP = Pfor all \gamma \in \Gamma and x \in V....
of a skew-symmetric matrix (note that it is not invariant under a general change of basis but rather under a proper orthogonalOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
transformation). As such, it is important in the theory of characteristic classCharacteristic classIn mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. In particular, it can be used to define the Euler classEuler classIn mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
which is used in the generalized Gauss-Bonnet theoremGeneralized Gauss-Bonnet theoremIn mathematics, the generalized Gauss–Bonnet theorem presents the Euler characteristic of a closed even-dimensional Riemannian manifold as an integral of a certain polynomial derived from its curvature...
.
- The number of perfect matchings in a planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
is given by a Pfaffian, hence is polynomial time computable via the FKT algorithmFKT algorithmThe FKT algorithm, named after Fisher, Kasteleyn, and Temperley, counts the number of perfect matchings in a planar graph in polynomial time. This same task is #P-complete for general graphs. Counting the number of matchings, even for planar graphs, is also #P-complete...
. This is surprising given that for general graphs, the problem is very difficult (so called #P-complete). This result is used to calculate the number of domino tilingDomino tilingA domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge...
s of a rectangle, the partition functionPartition function (statistical mechanics)Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
s in physics, or of Markov random fields in machine learningMachine learningMachine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, where the underlying graph is planar. It is also used to derive efficient algorithms for some otherwise seemingly intractable problems, including the efficient simulation of certain types of restricted quantum computation. Read Holographic algorithmHolographic algorithmIn computer science, a holographic algorithm is an algorithm that uses a holographic reduction. A holographic reduction is a reduction that preserves the number of solutions. These concepts were introduced by Leslie Valiant and are a natural type of reduction for #P problems.Holographic algorithms...
for more information.
External links
- Pfaffian at PlanetMath.org
- T. Jones, The Pfaffian and the Wedge Product (a demonstration of the proof of the Pfaffian/determinant relationship)
- R. Kenyon and A. OkounkovAndrei OkounkovAndrei Yuryevich Okounkov is a Russian mathematician who works on representation theory and its applications to algebraic geometry, mathematical physics, probability theory and special functions. He is currently a professor at Columbia University....
, What is ... a dimer?