Domino tiling
Encyclopedia
A domino tiling of a region in the Euclidean plane is a tessellation
of the region by domino
s, shapes formed by the union of two unit square
s meeting edge-to-edge. Equivalently, it is a matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.
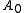with height 0, then for any node there is a path from 
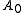to it. On this path define the height of each node 
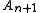(i.e. corners of the squares) to be the height of the previous node 
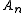plus one if the square on the right of the path from 
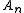to 
is black, and minus one else.
More details can be found in .
(1990) describes a test for determining whether a simply-connected region, formed as the union of unit squares in the plane, has a domino tiling. He forms an undirected graph that has as its vertices the points (x,y,z) in the three-dimensional integer lattice
, where each such point is connected to four neighbors: if x+y is even, then (x,y,z) is connected to (x+1,y,z+1), (x-1,y,z+1), (x,y+1,z-1), and (x,y-1,z-1), while if x+y is odd, then (x,y,z) is connected to (x+1,y,z-1), (x-1,y,z-1), (x,y+1,z+1), and (x,y-1,z+1). The boundary of the region, viewed as a sequence of integer points in the (x,y) plane, lifts uniquely (once a starting height is chosen) to a path in this three-dimensional graph. A necessary condition for this region to be tileable is that this path must close up to form a simple closed curve in three dimensions, however, this condition is not sufficient. Using more careful analysis of the boundary path, Thurston gave a criterion for tileability of a region that was sufficient as well as necessary.
-by-
rectangle with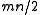 
dominoes, calculated independently by and , is given by
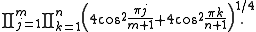
The sequence of values generated by this formula for squares with m = n = 0, 2, 4, 6, 8, 10, 12, ... is
These numbers can be found by writing them as the Pfaffian
of an mn by mn antisymmetric matrix whose eigenvalues can be found explicitly. This technique may be applied in many mathematics-related subjects, for example, in the classical, 2-dimensional computation of the dimer-dimer correlator function in statistical mechanics
.
The number of tilings of a region is very sensitive to boundary conditions, and can change dramatically with apparently insignificant changes in the shape of the region. This is illustrated by
the number of tilings of an Aztec diamond
of order n, where the number of tilings is 2(n+1)n/2. If this is replaced by the "augmented Aztec diamond" of order n with 3 long rows in the middle rather than 2, the
number of tilings drops to the much smaller number D(n,n), a Delannoy number
, which has only exponential rather than super-exponential growth in n. For the "reduced Aztec diamond" of order n with only one
long middle row, there is only one tiling.
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the region by domino
Domino (mathematics)
In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino....
s, shapes formed by the union of two unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
s meeting edge-to-edge. Equivalently, it is a matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.
Height functions
For some classes of tilings on a regular grid in two dimensions, it is possible to define a height function associating an integer to the nodes of the grid. For instance, draw a chessboard, fix a node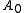 with height 0, then for any node there is a path from 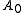to it. On this path define the height of each node 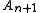(i.e. corners of the squares) to be the height of the previous node 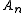plus one if the square on the right of the path from 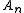to is black, and minus one else.More details can be found in .
Thurston's height condition
William ThurstonWilliam Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
(1990) describes a test for determining whether a simply-connected region, formed as the union of unit squares in the plane, has a domino tiling. He forms an undirected graph that has as its vertices the points (x,y,z) in the three-dimensional integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
, where each such point is connected to four neighbors: if x+y is even, then (x,y,z) is connected to (x+1,y,z+1), (x-1,y,z+1), (x,y+1,z-1), and (x,y-1,z-1), while if x+y is odd, then (x,y,z) is connected to (x+1,y,z-1), (x-1,y,z-1), (x,y+1,z+1), and (x,y-1,z+1). The boundary of the region, viewed as a sequence of integer points in the (x,y) plane, lifts uniquely (once a starting height is chosen) to a path in this three-dimensional graph. A necessary condition for this region to be tileable is that this path must close up to form a simple closed curve in three dimensions, however, this condition is not sufficient. Using more careful analysis of the boundary path, Thurston gave a criterion for tileability of a region that was sufficient as well as necessary.
Counting tilings of regions
The number of ways to cover a-by- rectangle with 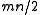dominoes, calculated independently by and , is given by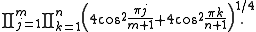The sequence of values generated by this formula for squares with m = n = 0, 2, 4, 6, 8, 10, 12, ... is
- 1, 2, 36, 6728, 12988816, 258584046368, 53060477521960000, ... .
These numbers can be found by writing them as the Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
of an mn by mn antisymmetric matrix whose eigenvalues can be found explicitly. This technique may be applied in many mathematics-related subjects, for example, in the classical, 2-dimensional computation of the dimer-dimer correlator function in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
the number of tilings of an Aztec diamond
Aztec diamond
In combinatorial mathematics, an Aztec diamond of order n consists of all squares of a square lattice whose centers satisfy |x| + |y| ≤ n...
of order n, where the number of tilings is 2(n+1)n/2. If this is replaced by the "augmented Aztec diamond" of order n with 3 long rows in the middle rather than 2, the
number of tilings drops to the much smaller number D(n,n), a Delannoy number
Delannoy number
In mathematics, a Delannoy number D describes the number of paths from the southwest corner of a rectangular grid to the northeast corner , using only single steps north, northeast, or east....
, which has only exponential rather than super-exponential growth in n. For the "reduced Aztec diamond" of order n with only one
long middle row, there is only one tiling.
See also
- Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
- Gaussian free fieldGaussian free fieldIn probability theory and statistical mechanics, the Gaussian free field is a Gaussian random field, a central model of random surfaces . A nice survey is ....
, the scaling limit of the height function in the generic situation (e.g., inside the inscribed disk of a large aztec diamond) - Mutilated chessboard problemMutilated chessboard problemThe mutilated chessboard problem is a tiling puzzle introduced by and discussed by Martin Gardner in his Scientific American column "Mathematical Games." The problem is as follows:...
, a puzzle concerning domino tiling of a 62-square subset of the chessboard - TatamiTatamiA is a type of mat used as a flooring material in traditional Japanese-style rooms. Traditionally made of rice straw to form the core , with a covering of woven soft rush straw, tatami are made in standard sizes, with the length exactly twice the width...
, floor mats in the shape of a domino that are used to tile the floors of Japanese rooms, with certain rules about how they may be placed