
Algebraic graph theory
Encyclopedia
Algebraic graph theory
is a branch of mathematics
in which algebra
ic methods are applied to problems about graphs
. This is in contrast to geometric
, combinatoric, or algorithmic approaches. There are three main branches of algebraic graph theory, involving the use of linear algebra
, the use of group theory
, and the study of graph invariants
.
. Especially, it studies the spectrum
of the adjacency matrix
, or the Laplacian matrix
of a graph (this part of algebraic graph theory is also called spectral graph theory
). For the Petersen graph
, for example, the spectrum of the adjacency matrix is (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Several theorems relate properties of the spectrum to other graph properties
. As a simple example, a connected
graph with diameter
D will have at least D+1 distinct values in its spectrum. Aspects
of graph spectra have been used in analysing the synchronizability of networks
.
, particularly automorphism groups
and geometric group theory
. The focus is placed on various families of graphs based on symmetry
(such as symmetric graph
s, vertex-transitive graph
s, edge-transitive graph
s, distance-transitive graph
s, distance-regular graph
s, and strongly regular graph
s), and on the inclusion relationships between these families. Certain of such categories of graphs are sparse enough that lists of graphs can be drawn up. By Frucht's theorem
, all groups
can be represented as the automorphism group of a connected graph (indeed, of a cubic graph
). Another connection with group theory is that, given any group, symmetrical graphs known as Cayley graph
s can be generated, and these have properties related to the structure of the group.
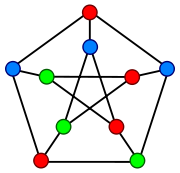 This second branch of algebraic graph theory is related to the first, since the symmetry properties of a graph are reflected in its spectrum. In particular, the spectrum of a highly symmetrical graph, such as the Petersen graph, has few distinct values (the Petersen graph has 3, which is the minimum possible, given its diameter). For Cayley graphs, the spectrum can be related directly to the structure of the group, in particular to its irreducible characters
This second branch of algebraic graph theory is related to the first, since the symmetry properties of a graph are reflected in its spectrum. In particular, the spectrum of a highly symmetrical graph, such as the Petersen graph, has few distinct values (the Petersen graph has 3, which is the minimum possible, given its diameter). For Cayley graphs, the spectrum can be related directly to the structure of the group, in particular to its irreducible characters
.
of graphs, and especially the chromatic polynomial
, the Tutte polynomial
and knot invariant
s. The chromatic polynomial of a graph, for example, counts the number of its proper vertex colorings. For the Petersen graph, this polynomial is . In particular, this means that the Petersen graph cannot be properly colored with one or two colors, but can be colored in 120 different ways with 3 colors. Much work in this area of algebraic graph theory was motivated by attempts to prove the four color theorem
. In particular, this means that the Petersen graph cannot be properly colored with one or two colors, but can be colored in 120 different ways with 3 colors. Much work in this area of algebraic graph theory was motivated by attempts to prove the four color theorem
. However, there are still many open problems, such as characterizing graphs which have the same chromatic polynomial, and determining which polynomials are chromatic.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
is a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
in which algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic methods are applied to problems about graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. This is in contrast to geometric
Geometric graph theory
In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...
, combinatoric, or algorithmic approaches. There are three main branches of algebraic graph theory, involving the use of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the use of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, and the study of graph invariants
Graph property
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...
.
Using linear algebra
The first branch of algebraic graph theory involves the study of graphs in connection with linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. Especially, it studies the spectrum
Eigendecomposition of a matrix
In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...
of the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
, or the Laplacian matrix
Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
of a graph (this part of algebraic graph theory is also called spectral graph theory
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
). For the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, for example, the spectrum of the adjacency matrix is (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Several theorems relate properties of the spectrum to other graph properties
Graph property
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...
. As a simple example, a connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
graph with diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
D will have at least D+1 distinct values in its spectrum. Aspects
Algebraic connectivity
The algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
of graph spectra have been used in analysing the synchronizability of networks
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
.
Using group theory
The second branch of algebraic graph theory involves the study of graphs in connection to group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, particularly automorphism groups
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
. The focus is placed on various families of graphs based on symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
(such as symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
s, vertex-transitive graph
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
s, edge-transitive graph
Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
s, distance-transitive graph
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
s, distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
s, and strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
s), and on the inclusion relationships between these families. Certain of such categories of graphs are sparse enough that lists of graphs can be drawn up. By Frucht's theorem
Frucht's theorem
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph...
, all groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be represented as the automorphism group of a connected graph (indeed, of a cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
). Another connection with group theory is that, given any group, symmetrical graphs known as Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s can be generated, and these have properties related to the structure of the group.


Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
.
Studying graph invariants
Finally, the third branch of algebraic graph theory concerns algebraic properties of invariantsGraph property
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...
of graphs, and especially the chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
, the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
and knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
s. The chromatic polynomial of a graph, for example, counts the number of its proper vertex colorings. For the Petersen graph, this polynomial is
 . In particular, this means that the Petersen graph cannot be properly colored with one or two colors, but can be colored in 120 different ways with 3 colors. Much work in this area of algebraic graph theory was motivated by attempts to prove the four color theorem
. In particular, this means that the Petersen graph cannot be properly colored with one or two colors, but can be colored in 120 different ways with 3 colors. Much work in this area of algebraic graph theory was motivated by attempts to prove the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. However, there are still many open problems, such as characterizing graphs which have the same chromatic polynomial, and determining which polynomials are chromatic.
See also
- Spectral graph theorySpectral graph theoryIn mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
- Algebraic combinatoricsAlgebraic combinatoricsAlgebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
- Algebraic connectivityAlgebraic connectivityThe algebraic connectivity of a graph G is the second-smallest eigenvalue of the Laplacian matrix of G. This eigenvalue is greater than 0 if and only if G is a connected graph. This is a corollary to the fact that the number of times 0 appears as an eigenvalue in the Laplacian is the number of...
- Dulmage–Mendelsohn decomposition
- Graph propertyGraph propertyIn graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...

