
Twistor theory
Encyclopedia
In theoretical
and mathematical physics
, twistor theory maps the geometric objects of conventional 3+1 space-time (Minkowski space
) into geometric objects in a 4 dimensional space with metric signature
(2,2). This space is called twistor space, and its complex
valued coordinates are called "twistors."
Twistor theory was first proposed by Roger Penrose
in 1967, as a possible path to a theory of quantum gravity
. The twistor approach is especially natural for solving the equations of motion of massless fields
of arbitrary spin
.
In 2003, Edward Witten
proposed to unite twistor and string theory
by embedding the topological B model
of string theory in twistor space. His objective was to model certain Yang-Mills amplitudes
. The resulting model has come to be known as twistor string theory (read below).
and the (2,2) metric signature
, and does not generalize to other dimensions or metric signatures. At the heart of twistor theory lies the isomorphism
between the conformal group
Spin(4,2) and SU(2,2), which is the group of unitary transformation
s of determinant
1 over a four dimensional complex vector space
. These transformations leave invariant a Hermitian norm of signature (2,2).
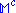 ,
,  ,
, 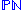 and
and  are all homogeneous spaces of the conformal group
are all homogeneous spaces of the conformal group
.
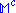 admits a conformal metric (i.e., an equivalence class of metric tensors under Weyl rescalings) with signature (+++−). Straight null rays map to straight null rays under
admits a conformal metric (i.e., an equivalence class of metric tensors under Weyl rescalings) with signature (+++−). Straight null rays map to straight null rays under
a conformal transformation and there is a unique canonical isomorphism
between null rays in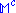 and points in
and points in 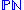 respecting the conformal group
respecting the conformal group
.
In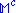 , it is the case that positive and negative frequency solutions cannot be locally separated. However, this is possible in twistor space.
, it is the case that positive and negative frequency solutions cannot be locally separated. However, this is possible in twistor space.
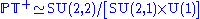
, its potential contributions to understanding the other fundamental interactions and particle physics
were less obvious.
Witten
(2003) proposed a connection between string theory
and twistor geometry, called twistor string theory. Witten (2004) built on this insight to propose a way to do string theory in twistor space, whose dimensionality is necessarily the same as that of 3+1 Minkowski spacetime. Hence twistor string theory is a possible way to eliminate the need for more than 3 spatial dimensions when doing (super)string theory. Although Witten has said that "I think twistor string theory is something that only partly works," his work has given new life to the twistor research program. For example, twistor string theory may simplify calculating scattering amplitude
s from Feynman diagram
s.
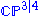 . Supertwistors are a supersymmetric
. Supertwistors are a supersymmetric
extension of twistors introduced by Alan Ferber in 1978. Along with the standard twistor degrees of freedom, a supertwistor contains N fermion
ic scalar
s, where N is the number of supersymmetries. The superconformal algebra
can be realized on supertwistor space.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, twistor theory maps the geometric objects of conventional 3+1 space-time (Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
) into geometric objects in a 4 dimensional space with metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(2,2). This space is called twistor space, and its complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued coordinates are called "twistors."
Twistor theory was first proposed by Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
in 1967, as a possible path to a theory of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. The twistor approach is especially natural for solving the equations of motion of massless fields
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of arbitrary spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
.
In 2003, Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
proposed to unite twistor and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
by embedding the topological B model
Topological string theory
In theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...
of string theory in twistor space. His objective was to model certain Yang-Mills amplitudes
S matrix
In physics, the scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process...
. The resulting model has come to be known as twistor string theory (read below).
Details
Twistor theory is unique to 4D Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
and the (2,2) metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
, and does not generalize to other dimensions or metric signatures. At the heart of twistor theory lies the isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between the conformal group
Conformal group
In mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
Spin(4,2) and SU(2,2), which is the group of unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
s of determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 over a four dimensional complex vector space
Complex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
. These transformations leave invariant a Hermitian norm of signature (2,2).
-
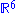 is the real 6D vector space corresponding to the vector representation of Spin(4,2).
is the real 6D vector space corresponding to the vector representation of Spin(4,2).
-
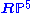 is the real 5D projective representationProjective representationIn the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
is the real 5D projective representationProjective representationIn the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
corresponding to the equivalence class of nonzero points in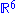 under scalar multiplication.
under scalar multiplication.
-
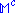 corresponds to the subspace of
corresponds to the subspace of 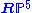 corresponding to vectors of zero norm. This is conformally compactified Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
corresponding to vectors of zero norm. This is conformally compactified Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
-
 is the 4D complex Weyl spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
is the 4D complex Weyl spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
representation and is called twistor space. It has an invariant Hermitian sesquilinear norm of signature (2,2).
-
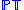 is a 3D complex manifold corresponding to projective twistor space.
is a 3D complex manifold corresponding to projective twistor space.
-
 is the subspace of
is the subspace of 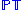 corresponding to projective twistors with positive norm (the sign of the norm, but not its absolute value is projectively invariant). This is a 3D complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
corresponding to projective twistors with positive norm (the sign of the norm, but not its absolute value is projectively invariant). This is a 3D complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
.
-
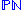 is the subspace of
is the subspace of 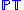 consisting of null projective twistors (zero norm). This is a real-complex manifold (i.e., it has 5 real dimensions, with four of the real dimensions having a complex structure making them two complex dimensions).
consisting of null projective twistors (zero norm). This is a real-complex manifold (i.e., it has 5 real dimensions, with four of the real dimensions having a complex structure making them two complex dimensions).
-
 is the subspace of
is the subspace of 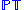 of projective twistors with negative norm.
of projective twistors with negative norm.
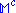 ,
,  ,
, 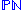 and
and  are all homogeneous spaces of the conformal group
are all homogeneous spaces of the conformal groupConformal group
In mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
.
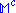 admits a conformal metric (i.e., an equivalence class of metric tensors under Weyl rescalings) with signature (+++−). Straight null rays map to straight null rays under
admits a conformal metric (i.e., an equivalence class of metric tensors under Weyl rescalings) with signature (+++−). Straight null rays map to straight null rays undera conformal transformation and there is a unique canonical isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between null rays in
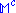 and points in
and points in 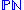 respecting the conformal group
respecting the conformal groupConformal group
In mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
.
In
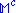 , it is the case that positive and negative frequency solutions cannot be locally separated. However, this is possible in twistor space.
, it is the case that positive and negative frequency solutions cannot be locally separated. However, this is possible in twistor space.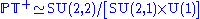
Twistor string theory
For many years after Penrose's foundational 1967 paper, twistor theory progressed slowly, in part because of mathematical challenges. Twistor theory also seemed unrelated to ideas in mainstream physics. While twistor theory appeared to say something about quantum gravityQuantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, its potential contributions to understanding the other fundamental interactions and particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
were less obvious.
Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
(2003) proposed a connection between string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
and twistor geometry, called twistor string theory. Witten (2004) built on this insight to propose a way to do string theory in twistor space, whose dimensionality is necessarily the same as that of 3+1 Minkowski spacetime. Hence twistor string theory is a possible way to eliminate the need for more than 3 spatial dimensions when doing (super)string theory. Although Witten has said that "I think twistor string theory is something that only partly works," his work has given new life to the twistor research program. For example, twistor string theory may simplify calculating scattering amplitude
Scattering amplitude
In quantum physics, the scattering amplitude is the amplitude of the outgoing spherical wave relative to the incoming plane wave in the stationary-state scattering process...
s from Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s.
Supertwistors
Witten's twistor string theory is defined on the supertwistor space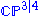 . Supertwistors are a supersymmetric
. Supertwistors are a supersymmetricSupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
extension of twistors introduced by Alan Ferber in 1978. Along with the standard twistor degrees of freedom, a supertwistor contains N fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
s, where N is the number of supersymmetries. The superconformal algebra
Superconformal algebra
In theoretical physics, the superconformal algebra is a graded Lie algebra or superalgebra that combines the conformal algebra and supersymmetry. It generates the superconformal group in some cases .In two dimensions, the superconformal algebra is infinite-dimensional...
can be realized on supertwistor space.
Further reading
- Baird, Paul "An Introduction To Twistors"
- Penrose, Roger (1987) "On the Origins of Twistor Theory" in Gravitation and Geometry, a volume in honour of I. Robinson. Naples: Bibliopolis.
- Penrose, Roger (1999) "The Central Programme of Twistor Theory," Chaos, Solitons and Fractals 10: 581-611.
- Arkani-Hamed, NimaNima Arkani-HamedNima Arkani-Hamed is a leading Canadian American theoretical physicist with interests in high-energy physics, string theory and cosmology....
; Cachazo, Freddy; Cheung, Clifford; Kaplan, Jared (2009) "The S-Matrix in Twistor Space."
External links
- Penrose, RogerRoger PenroseSir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
(1999) "Einstein's Equation and Twistor Theory: Recent Developments" - Penrose, Roger; Hadrovich, Fedja. "Twistor Theory."
- Dunajski, Maciej, "Twistor Theory and Differential Equations."
- Hadrovich, Fedja, "Twistor primer."
- Andrew HodgesAndrew HodgesAndrew Hodges is a mathematician, an author and a pioneer of the gay liberation movement of the 1970s.For the past decades , Hodges has focused his research activities on the twistor theory — the new approach to the problems of fundamental physics pioneered by the mathematician Roger...
, "Twistor Theory and the Twistor Programme." Includes many links. - Huggett, Stephen (2005) "The Elements of Twistor Theory."
- Richard JozsaRichard JozsaRichard Jozsa is the holder of the Leigh Trapnell Chair in Quantum Physics at the University of Cambridge. His research area is quantum information science; a pioneer of this field, he is the co-author of the Deutsch-Jozsa quantum algorithm and one of the co-inventors of quantum teleportation...
(1976) "Applications of Sheaf Cohomology in Twistor Theory." - Mason, L. J., "The twistor programme and twistor strings:From twistor strings to quantum gravity?"
- Sämann, Christian (2006) "Aspects of Twistor Geometry and Supersymmetric Field Theories within Superstring Theory."
- Sparling, George (1999) "On Time Asymmetry."
- Spradlin, Marcus, "Progress And Prospects In Twistor String Theory."
- MathWorld - Twistors.
- Universe Review "Twistor Theory."
- Twistor newsletter archives

