
Isometry (Riemannian geometry)
Encyclopedia
In the study of Riemannian geometry
in mathematics
, a local isometry from one (pseudo
-)Riemannian manifold
to another is a map which pulls back the metric tensor
on the second manifold to the metric tensor on the first. When such a map is also a diffeomorphism
, such a map is called an isometry (or isometric isomorphism), and provides a notion of isomorphism
("sameness") in the category
Rm of Riemannian manifolds.
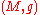 and
and  be two Riemannian manifolds, and let
be two Riemannian manifolds, and let 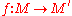 be a diffeomorphism. Then
be a diffeomorphism. Then  is called an isometry (or isometric isomorphism) if
is called an isometry (or isometric isomorphism) if
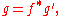
where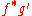 denotes the pullback of the rank (0, 2) metric tensor
denotes the pullback of the rank (0, 2) metric tensor 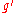 by
by  . Equivalently, in terms of the push-forward
. Equivalently, in terms of the push-forward 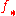 , we have that for any two vector fields
, we have that for any two vector fields  on
on  (i.e. sections of the tangent bundle
(i.e. sections of the tangent bundle
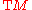 ),
),
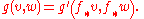
If is a local diffeomorphism
is a local diffeomorphism
such that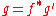 , then
, then  is called a local isometry.
is called a local isometry.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a local isometry from one (pseudo
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
-)Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
to another is a map which pulls back the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on the second manifold to the metric tensor on the first. When such a map is also a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
, such a map is called an isometry (or isometric isomorphism), and provides a notion of isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
("sameness") in the category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
Rm of Riemannian manifolds.
Definition
Let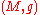 and
and  be two Riemannian manifolds, and let
be two Riemannian manifolds, and let 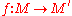 be a diffeomorphism. Then
be a diffeomorphism. Then  is called an isometry (or isometric isomorphism) if
is called an isometry (or isometric isomorphism) if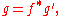
where
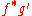 denotes the pullback of the rank (0, 2) metric tensor
denotes the pullback of the rank (0, 2) metric tensor 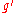 by
by  . Equivalently, in terms of the push-forward
. Equivalently, in terms of the push-forward 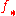 , we have that for any two vector fields
, we have that for any two vector fields  on
on  (i.e. sections of the tangent bundle
(i.e. sections of the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
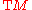 ),
),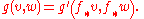
If
 is a local diffeomorphism
is a local diffeomorphismLocal diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
such that
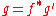 , then
, then  is called a local isometry.
is called a local isometry.

