
Cremona group
Encyclopedia
In mathematics
, in birational geometry
, the Cremona group (named for Luigi Cremona
) of order over a field
over a field
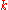 is the group of birational automorphisms of the n-dimensional projective space
is the group of birational automorphisms of the n-dimensional projective space
over k. It is denoted by Cr(Pn(k))
or Bir(Pn(k)) or Crn(k).
The Cremona group is naturally identified with the automorphism group of the function field
over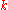 in
in  indeterminates, or in other words a pure transcendental extension of k, with transcendence degree n.
indeterminates, or in other words a pure transcendental extension of k, with transcendence degree n.
The projective general linear group of order , of projective transformations, is contained in the Cremona group of order
, of projective transformations, is contained in the Cremona group of order  . The two are equal only when
. The two are equal only when  , in which case both the numerator and the denominator of a transformation must be linear.
, in which case both the numerator and the denominator of a transformation must be linear.
In two dimensions, the Cremona group is generated by the standard quadratic transformation, along with PGL(3, k), provided that k is an algebraically closed field
.
The problem of describing the Cremona group in three dimensions and higher has still not been settled.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in birational geometry
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
, the Cremona group (named for Luigi Cremona
Luigi Cremona
Luigi Cremona was an Italian mathematician. His life was devoted to the study of geometry and reforming advanced mathematical teaching in Italy. His reputation mainly rests on his Introduzione ad una teoria geometrica delle curve piane...
) of order
 over a field
over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
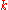 is the group of birational automorphisms of the n-dimensional projective space
is the group of birational automorphisms of the n-dimensional projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
over k. It is denoted by Cr(Pn(k))
or Bir(Pn(k)) or Crn(k).
The Cremona group is naturally identified with the automorphism group of the function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
over
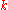 in
in  indeterminates, or in other words a pure transcendental extension of k, with transcendence degree n.
indeterminates, or in other words a pure transcendental extension of k, with transcendence degree n.The projective general linear group of order
 , of projective transformations, is contained in the Cremona group of order
, of projective transformations, is contained in the Cremona group of order  . The two are equal only when
. The two are equal only when  , in which case both the numerator and the denominator of a transformation must be linear.
, in which case both the numerator and the denominator of a transformation must be linear.In two dimensions, the Cremona group is generated by the standard quadratic transformation, along with PGL(3, k), provided that k is an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
.
The problem of describing the Cremona group in three dimensions and higher has still not been settled.

