
Cylinder set
Encyclopedia
In mathematics
, a cylinder set is the natural open set of a product topology
. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set. If V is a finite set, then each element of V can be represented by a letter, and the countable product can be represented by the collection of strings
of letters.
 of topological space
of topological space
s , indexed by some index
, indexed by some index  . The canonical projection is the function
. The canonical projection is the function  that selects out the
that selects out the  component of the product. Then, given any open set
component of the product. Then, given any open set
 , the preimage
, the preimage 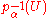 is called an open cylinder. The intersection of a finite number of open cylinders is a cylinder set. The collection of open cylinders form a subbase
is called an open cylinder. The intersection of a finite number of open cylinders is a cylinder set. The collection of open cylinders form a subbase
of the product topology
on ; the collection of all cylinder sets thus form a basis.
; the collection of all cylinder sets thus form a basis.
The restriction that the cylinder set be the intersection of a finite number of open cylinders is important; allowing infinite intersections generally results in a finer topology. In this case, the resulting topology is the box topology
; cylinder sets are never Hilbert cube
s.
 be a finite set, containing n objects or letters. The collection of all bi-infinite strings in these letters is denoted by
be a finite set, containing n objects or letters. The collection of all bi-infinite strings in these letters is denoted by
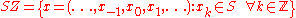
where denotes the integer
denotes the integer
s. The natural topology on is the discrete topology. Basic open sets in the discrete topology consist of individual letters; thus, the open cylinders of the product topology on
is the discrete topology. Basic open sets in the discrete topology consist of individual letters; thus, the open cylinders of the product topology on  are
are

The intersections a finite number of open cylinders are the cylinder sets

Cylinder sets are clopen set
s. As elements of the topology, cylinder sets are by definition open sets. The complement of an open set is a closed set, but the complement of a cylinder set is a union of cylinders, and so cylinder sets are also closed, and are thus clopen. As a result, the topology satisfies the axioms of a sigma algebra.
 over a field K (such as the real or complex numbers), the cylinder sets may be defined as
over a field K (such as the real or complex numbers), the cylinder sets may be defined as

where is a Borel set
is a Borel set
in , and each
, and each 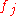 is a linear functional on
is a linear functional on  ; that is,
; that is,  , the algebraic dual space
, the algebraic dual space
to . When dealing with topological vector space
. When dealing with topological vector space
s, the definition is made instead for elements , the continuous dual space. That is, the functionals
, the continuous dual space. That is, the functionals 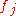 are taken to be continuous linear functionals. The article on dual space
are taken to be continuous linear functionals. The article on dual space
s discusses the differences between the algebraic and the continuous dual spaces.
 and occur frequently in the study of symbolic dynamics
and occur frequently in the study of symbolic dynamics
; see, for example, subshift of finite type
. Cylinder sets are often used to define a measure; for example, the measure of a cylinder set of length m might be given by 1/m or by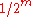 . Since strings in
. Since strings in  can be considered to be p-adic number
can be considered to be p-adic number
s, some of the theory of p-adic numbers can be applied to cylinder sets, and in particular, the definition of p-adic measures and p-adic metrics apply to cylinder sets. Cylinder sets may be used to define a metric
on the space: for example, one says that two strings are ε-close if a fraction 1-ε of the letters in the strings match.
Cylinder sets over topological vector spaces are the core ingredient in the formal definition of the Feynman path integral or functional integral of quantum field theory
, and the partition function
of statistical mechanics
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cylinder set is the natural open set of a product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set. If V is a finite set, then each element of V can be represented by a letter, and the countable product can be represented by the collection of strings
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of letters.
General definition
Consider the cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
 of topological space
of topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s
 , indexed by some index
, indexed by some index  . The canonical projection is the function
. The canonical projection is the function  that selects out the
that selects out the  component of the product. Then, given any open set
component of the product. Then, given any open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
 , the preimage
, the preimage 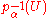 is called an open cylinder. The intersection of a finite number of open cylinders is a cylinder set. The collection of open cylinders form a subbase
is called an open cylinder. The intersection of a finite number of open cylinders is a cylinder set. The collection of open cylinders form a subbaseSubbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
of the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
on
 ; the collection of all cylinder sets thus form a basis.
; the collection of all cylinder sets thus form a basis.The restriction that the cylinder set be the intersection of a finite number of open cylinders is important; allowing infinite intersections generally results in a finer topology. In this case, the resulting topology is the box topology
Box topology
In topology, the cartesian product of topological spaces can be given several different topologies. The canonical one is the product topology, because it fits rather nicely with the categorical notion of a product. Another possibility is the box topology. The box topology has a somewhat more...
; cylinder sets are never Hilbert cube
Hilbert cube
In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
s.
Definition for infinite products of finite, discrete sets
Let be a finite set, containing n objects or letters. The collection of all bi-infinite strings in these letters is denoted by
be a finite set, containing n objects or letters. The collection of all bi-infinite strings in these letters is denoted by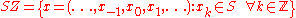
where
 denotes the integer
denotes the integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. The natural topology on
 is the discrete topology. Basic open sets in the discrete topology consist of individual letters; thus, the open cylinders of the product topology on
is the discrete topology. Basic open sets in the discrete topology consist of individual letters; thus, the open cylinders of the product topology on  are
are
The intersections a finite number of open cylinders are the cylinder sets

Cylinder sets are clopen set
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
s. As elements of the topology, cylinder sets are by definition open sets. The complement of an open set is a closed set, but the complement of a cylinder set is a union of cylinders, and so cylinder sets are also closed, and are thus clopen. As a result, the topology satisfies the axioms of a sigma algebra.
Definition for vector spaces
Given a finite or infinite-dimensional vector space over a field K (such as the real or complex numbers), the cylinder sets may be defined as
over a field K (such as the real or complex numbers), the cylinder sets may be defined as
where
 is a Borel set
is a Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
in
 , and each
, and each 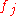 is a linear functional on
is a linear functional on  ; that is,
; that is,  , the algebraic dual space
, the algebraic dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
to
 . When dealing with topological vector space
. When dealing with topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, the definition is made instead for elements
 , the continuous dual space. That is, the functionals
, the continuous dual space. That is, the functionals 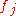 are taken to be continuous linear functionals. The article on dual space
are taken to be continuous linear functionals. The article on dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s discusses the differences between the algebraic and the continuous dual spaces.
Applications
Cylinder sets are often used to define a topology on sets that are subsets of and occur frequently in the study of symbolic dynamics
and occur frequently in the study of symbolic dynamicsSymbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
; see, for example, subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
. Cylinder sets are often used to define a measure; for example, the measure of a cylinder set of length m might be given by 1/m or by
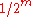 . Since strings in
. Since strings in  can be considered to be p-adic number
can be considered to be p-adic numberP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s, some of the theory of p-adic numbers can be applied to cylinder sets, and in particular, the definition of p-adic measures and p-adic metrics apply to cylinder sets. Cylinder sets may be used to define a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the space: for example, one says that two strings are ε-close if a fraction 1-ε of the letters in the strings match.
Cylinder sets over topological vector spaces are the core ingredient in the formal definition of the Feynman path integral or functional integral of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, and the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.

