Geometrical optics
Encyclopedia
Geometrical optics, or ray optics, describes light
propagation
in terms of "rays
". The "ray" in geometric optics is an abstraction
, or "instrument
", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in a homogeneous medium. Rays bend (and may split in two) at the interface between two dissimilar media, may curve in a medium where the refractive index
changes, and may be absorbed and reflected. Geometrical optics provides rules, which may depend on the color (wavelength) of the ray, for propagating these rays through an optical system. This is a significant simplification of optics that fails to account for optical effects such as diffraction
and interference. It is an excellent approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging
, including optical aberrations.
or curve
that is perpendicular
to the light's wavefront
s (and is therefore collinear with the wave vector
).
A slightly more rigorous definition of a light ray follows from Fermat's principle
, which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.
Geometrical optics is often simplified by making the paraxial approximation
, or "small angle approximation." The mathematical behavior then becomes linear
, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics
and paraxial ray tracing
, which are used to find basic properties of optical systems, such as approximate image
and object positions and magnification
s.
 Glossy surfaces such as mirror
Glossy surfaces such as mirror
s reflect light in a simple, predictable way. This allows for production of reflected images that can be associated with an actual (real
) or extrapolated (virtual
) location in space.
With such surfaces, the direction of the reflected ray is determined by the angle the incident ray makes with the surface normal
, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal. This is known as the Law of Reflection.
For flat mirrors
, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. (The magnification
of a flat mirror is equal to one.) The law also implies that mirror image
s are parity inverted
, which is perceived as a left-right inversion.
Mirrors with curved surfaces
can be modeled by ray tracing
and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces
, parallel rays incident on the mirror produce reflected rays that converge at a common focus
. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration
. Curved mirrors can form images with magnification greater than or less than one, and the image can be upright or inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.
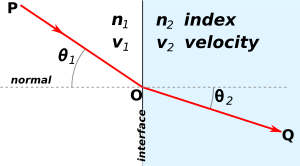 Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction
Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction 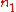 and another medium with index of refraction
and another medium with index of refraction 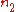 . In such situations, Snell's Law
. In such situations, Snell's Law
describes the resulting deflection of the light ray:

where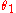 and
and 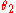 are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:

where and
and 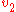 are the wave velocities through the respective media.
are the wave velocities through the respective media.
Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called total internal reflection
and allows for fiber optics technology. As light signals travel down a fiber optic cable, it undergoes total internal reflection allowing for essentially no light lost over the length of the cable. It is also possible to produce polarized light rays using a combination of reflection and refraction: When a refracted ray and the reflected ray form a right angle
, the reflected ray has the property of "plane polarization". The angle of incidence required for such a scenario is known as Brewster's angle
.
Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism
results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce dispersion
spectra
that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton
.
Some media have an index of refraction which varies gradually with position and, thus, light rays curve through the medium rather than travel in straight lines. This effect is what is responsible for mirage
s seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a varying index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including photocopiers and scanners
. The phenomenon is studied in the field of gradient-index optics.
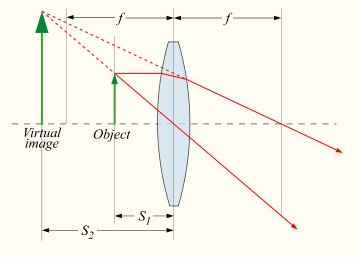 A device which produces converging or diverging light rays due to refraction is known as a lens
A device which produces converging or diverging light rays due to refraction is known as a lens
. Thin lenses produce focal points on either side that can be modeled using the lensmaker's equation. In general, two types of lenses exist: convex lenses, which cause parallel light rays to converge, and concave lenses, which cause parallel light rays to diverge. The detailed prediction of how images are produced by these lenses can be made using ray-tracing similar to curved mirrors. Similarly to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length ( ) and object distance (
) and object distance ( ):
):
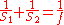
where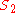 is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens. The focal length f is considered negative for concave lenses.
is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens. The focal length f is considered negative for concave lenses.
Incoming parallel rays are focused by a convex lens into an inverted real image one focal length from the lens, on the far side of the lens. Rays from an object at finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens. With concave lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at an upright virtual image one focal length from the lens, on the same side of the lens that the parallel rays are approaching on. Rays from an object at finite distance are associated with a virtual image that is closer to the lens than the focal length, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens.
Likewise, the magnification of a lens is given by
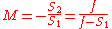
where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.
Lenses suffer from aberrations that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light (chromatic aberration
).
limit for solutions to hyperbolic partial differential equation
s. In this short-wavelength limit, it is possible to approximate the solution locally by
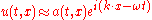
where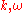 satisfy a dispersion relation
satisfy a dispersion relation
, and the amplitude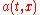 varies slowly. More precisely, the leading order solution takes the form
varies slowly. More precisely, the leading order solution takes the form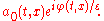
The phase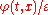 can be linearized to recover large wavenumber
can be linearized to recover large wavenumber 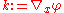 , and frequency
, and frequency 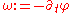 . The amplitude
. The amplitude  satisfies a transport equation. The small parameter
satisfies a transport equation. The small parameter  enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, refraction
enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, refraction
does not take place. The motivation for this technique comes from studying the typical scenario of light propagation where short wavelength light travels along rays that minimize (more or less) its travel time. Its full application requires tools from microlocal analysis
.

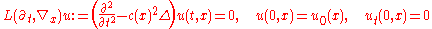
assume an asymptotic series solution of the form

Check that
with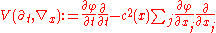
Plugging the series into this equation, and equating powers of , the most singular term
, the most singular term  satisfies the eikonal equation
satisfies the eikonal equation
(in this case called a dispersion relation),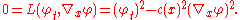
To order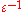 , the leading order amplitude must satisfy a transport equation
, the leading order amplitude must satisfy a transport equation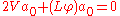
With the definition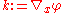 ,
, 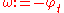 , the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution
, the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution 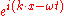 into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed
into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed  is non-constant. However, it can be shown that the amplitude
is non-constant. However, it can be shown that the amplitude  and phase
and phase 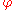 are smooth, so that on a local scale there are plane waves.
are smooth, so that on a local scale there are plane waves.
To justify this technique, the remaining terms are must be shown to be small in some sense. This can be done using energy estimates, and an assumption of rapidly oscillating initial conditions. It also must be shown that the series converges in some sense.
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
in terms of "rays
Ray (optics)
In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...
". The "ray" in geometric optics is an abstraction
Abstract object
An abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
, or "instrument
Instrumentalism
In the philosophy of science, instrumentalism is the view that a scientific theory is a useful instrument in understanding the world. A concept or theory should be evaluated by how effectively it explains and predicts phenomena, as opposed to how accurately it describes objective...
", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in a homogeneous medium. Rays bend (and may split in two) at the interface between two dissimilar media, may curve in a medium where the refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
changes, and may be absorbed and reflected. Geometrical optics provides rules, which may depend on the color (wavelength) of the ray, for propagating these rays through an optical system. This is a significant simplification of optics that fails to account for optical effects such as diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
and interference. It is an excellent approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
, including optical aberrations.
Explanation
A light ray is a lineLine (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
or curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
that is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the light's wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
s (and is therefore collinear with the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
).
A slightly more rigorous definition of a light ray follows from Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
, which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.
Geometrical optics is often simplified by making the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
, or "small angle approximation." The mathematical behavior then becomes linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics
Gaussian optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. In this approximation, trigonometric functions can...
and paraxial ray tracing
Ray tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces,...
, which are used to find basic properties of optical systems, such as approximate image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
and object positions and magnification
Magnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
s.
Reflection

Mirror
A mirror is an object that reflects light or sound in a way that preserves much of its original quality prior to its contact with the mirror. Some mirrors also filter out some wavelengths, while preserving other wavelengths in the reflection...
s reflect light in a simple, predictable way. This allows for production of reflected images that can be associated with an actual (real
Real image
In optics, a real image is a representation of an object in which the perceived location is actually a point of convergence of the rays of light that make up the image. If a screen is placed in the plane of a real image the image will generally become visible on the screen...
) or extrapolated (virtual
Virtual image
In optics, a virtual image is an image in which the outgoing rays from a point on the object always diverge. It will appear to converge in or behind the optical device . A simple example is a flat mirror where the image of oneself is perceived at twice the distance from oneself to the mirror...
) location in space.
With such surfaces, the direction of the reflected ray is determined by the angle the incident ray makes with the surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal. This is known as the Law of Reflection.
For flat mirrors
Plane mirror
A plane mirror is a mirror with a plane reflective surface.For light rays striking a plane mirror, the angle of reflection equals the angle of incidence...
, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. (The magnification
Magnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
of a flat mirror is equal to one.) The law also implies that mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
s are parity inverted
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
, which is perceived as a left-right inversion.
Mirrors with curved surfaces
Curved mirror
A curved mirror is a mirror with a curved reflective surface, which may be either convex or concave . Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices...
can be modeled by ray tracing
Ray tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces,...
and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces
Parabolic reflector
A parabolic reflector is a reflective device used to collect or project energy such as light, sound, or radio waves. Its shape is that of a circular paraboloid, that is, the surface generated by a parabola revolving around its axis...
, parallel rays incident on the mirror produce reflected rays that converge at a common focus
Focus (optics)
In geometrical optics, a focus, also called an image point, is the point where light rays originating from a point on the object converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the blur circle. This non-ideal focusing may be caused by...
. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration
Spherical aberration
thumb|right|Spherical aberration. A perfect lens focuses all incoming rays to a point on the [[Optical axis|optic axis]]. A real lens with spherical surfaces suffers from spherical aberration: it focuses rays more tightly if they enter it far from the optic axis than if they enter closer to the...
. Curved mirrors can form images with magnification greater than or less than one, and the image can be upright or inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.
Refraction

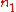 and another medium with index of refraction
and another medium with index of refraction 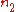 . In such situations, Snell's Law
. In such situations, Snell's LawSnell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
describes the resulting deflection of the light ray:

where
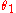 and
and 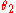 are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
are the angles between the normal (to the interface) and the incident and refracted waves, respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
where
 and
and 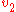 are the wave velocities through the respective media.
are the wave velocities through the respective media.Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called total internal reflection
Total internal reflection
Total internal reflection is an optical phenomenon that happens when a ray of light strikes a medium boundary at an angle larger than a particular critical angle with respect to the normal to the surface. If the refractive index is lower on the other side of the boundary and the incident angle is...
and allows for fiber optics technology. As light signals travel down a fiber optic cable, it undergoes total internal reflection allowing for essentially no light lost over the length of the cable. It is also possible to produce polarized light rays using a combination of reflection and refraction: When a refracted ray and the reflected ray form a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
, the reflected ray has the property of "plane polarization". The angle of incidence required for such a scenario is known as Brewster's angle
Brewster's angle
Brewster's angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly...
.
Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism
Prism (optics)
In optics, a prism is a transparent optical element with flat, polished surfaces that refract light. The exact angles between the surfaces depend on the application. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides, and in colloquial use...
results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
spectra
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
.
Some media have an index of refraction which varies gradually with position and, thus, light rays curve through the medium rather than travel in straight lines. This effect is what is responsible for mirage
Mirage
A mirage is a naturally occurring optical phenomenon in which light rays are bent to produce a displaced image of distant objects or the sky. The word comes to English via the French mirage, from the Latin mirare, meaning "to look at, to wonder at"...
s seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a varying index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including photocopiers and scanners
Scanners
Scanners is a 1981 science-fiction horror film written and directed by David Cronenberg and starring Jennifer O'Neill, Stephen Lack, Michael Ironside, and Patrick McGoohan...
. The phenomenon is studied in the field of gradient-index optics.

Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
. Thin lenses produce focal points on either side that can be modeled using the lensmaker's equation. In general, two types of lenses exist: convex lenses, which cause parallel light rays to converge, and concave lenses, which cause parallel light rays to diverge. The detailed prediction of how images are produced by these lenses can be made using ray-tracing similar to curved mirrors. Similarly to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length (
 ) and object distance (
) and object distance ( ):
):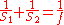
where
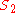 is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens. The focal length f is considered negative for concave lenses.
is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens. The focal length f is considered negative for concave lenses.Incoming parallel rays are focused by a convex lens into an inverted real image one focal length from the lens, on the far side of the lens. Rays from an object at finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens. With concave lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at an upright virtual image one focal length from the lens, on the same side of the lens that the parallel rays are approaching on. Rays from an object at finite distance are associated with a virtual image that is closer to the lens than the focal length, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens.
Likewise, the magnification of a lens is given by
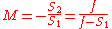
where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.
Lenses suffer from aberrations that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light (chromatic aberration
Chromatic aberration
In optics, chromatic aberration is a type of distortion in which there is a failure of a lens to focus all colors to the same convergence point. It occurs because lenses have a different refractive index for different wavelengths of light...
).
Underlying mathematics
As a mathematical study, geometrical optics emerges as a short-wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
limit for solutions to hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s. In this short-wavelength limit, it is possible to approximate the solution locally by
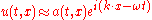
where
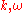 satisfy a dispersion relation
satisfy a dispersion relationDispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
, and the amplitude
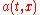 varies slowly. More precisely, the leading order solution takes the form
varies slowly. More precisely, the leading order solution takes the form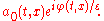
The phase
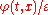 can be linearized to recover large wavenumber
can be linearized to recover large wavenumber 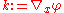 , and frequency
, and frequency 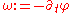 . The amplitude
. The amplitude  satisfies a transport equation. The small parameter
satisfies a transport equation. The small parameter  enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, refraction
enters the scene due to highly oscillatory initial conditions. Thus, when initial conditions oscillate much faster than the coefficients of the differential equation, solutions will be highly oscillatory, and transported along rays. Assuming coefficients in the differential equation are smooth, the rays will be too. In other words, refractionRefraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
does not take place. The motivation for this technique comes from studying the typical scenario of light propagation where short wavelength light travels along rays that minimize (more or less) its travel time. Its full application requires tools from microlocal analysis
Microlocal analysis
In mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
.
A simple example
Starting with the wave equation for
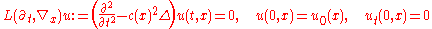
assume an asymptotic series solution of the form

Check that

with
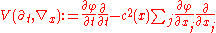
Plugging the series into this equation, and equating powers of
 , the most singular term
, the most singular term  satisfies the eikonal equation
satisfies the eikonal equationEikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
(in this case called a dispersion relation),
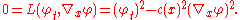
To order
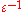 , the leading order amplitude must satisfy a transport equation
, the leading order amplitude must satisfy a transport equation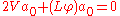
With the definition
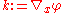 ,
, 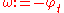 , the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution
, the eikonal equation is precisely the dispersion relation that results by plugging the plane wave solution 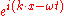 into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed
into the wave equation. The value of this more complicated expansion is that plane waves cannot be solutions when the wavespeed  is non-constant. However, it can be shown that the amplitude
is non-constant. However, it can be shown that the amplitude  and phase
and phase 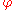 are smooth, so that on a local scale there are plane waves.
are smooth, so that on a local scale there are plane waves.To justify this technique, the remaining terms are must be shown to be small in some sense. This can be done using energy estimates, and an assumption of rapidly oscillating initial conditions. It also must be shown that the series converges in some sense.

