
Particle number operator
Encyclopedia
In quantum mechanics
, for systems where the total number of particles
may not be preserved, the number operator is the observable
that counts the number of particles.
The number operator acts on Fock space
. Given a Fock state
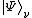 composed of single-particle basis state
composed of single-particle basis state
s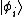 :
:

with creation and annihilation operators
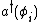 and
and 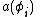 we define the number operator
we define the number operator 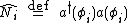 and we have:
and we have:
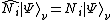
where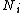 is the number of particles in state
is the number of particles in state 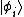 . The above equality can be proven by noting that
. The above equality can be proven by noting that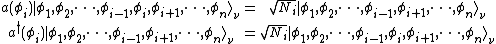
then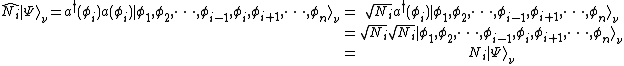
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, for systems where the total number of particles
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
may not be preserved, the number operator is the observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
that counts the number of particles.
The number operator acts on Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
. Given a Fock state
Fock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
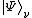 composed of single-particle basis state
composed of single-particle basis stateBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
s
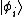 :
:
with creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
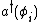 and
and 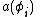 we define the number operator
we define the number operator 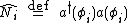 and we have:
and we have: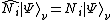
where
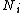 is the number of particles in state
is the number of particles in state 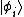 . The above equality can be proven by noting that
. The above equality can be proven by noting that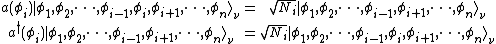
then
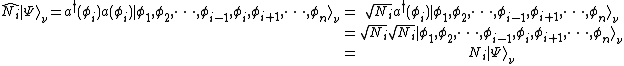
See also
- Harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
- Quantum harmonic oscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
- Second quantization
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Particle numberParticle numberThe particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...

