
Microstate (statistical mechanics)
Encyclopedia
In statistical mechanics
, a microstate is a specific microscopic configuration of a thermodynamic system
that the system may occupy with a certain probability in the course of its thermal fluctuations
. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature
and pressure
.
A macrostate is characterized by a probability distribution
of possible states across a certain statistical ensemble
of all microstates. This distribution describes the probability
of finding the system in a certain microstate. In the thermodynamic limit
, the microstates visited by a macroscopic system during its fluctuations all have the same macroscopic properties.
At any moment a system is distributed across an ensemble of N microstates, each denoted by i, and having a probability of occupation pi, and an energy . These microstates form a discrete set as defined by quantum statistical mechanics
. These microstates form a discrete set as defined by quantum statistical mechanics
, and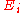 is an energy level
is an energy level
of the system.
of the system's energy
This is a microscopic statement of the first law of thermodynamics
.
exclusively depends on the probabilities of the microstates and is defined as
where is Boltzmann's constant.
is Boltzmann's constant.
Entropy is formulated by the second law of thermodynamics
. The third law of thermodynamics
is consistent with this definition, since zero entropy means that the macrostate of the system reduces to a single microstate.
is the energy transfer associated with a disordered, microscopic action on the system, associated with jumps in energy level
s of the system.
Work
is the energy transfer associated to the effect of an ordered, macroscopic action on the system. If this action acts very slowly then the Adiabatic theorem
implies that this will not cause a jump in the energy level of the system. The internal energy of the system can only change due to a change of the energies of the system's energy levels.
The microscopic definitions of heat and work are the following:
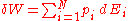
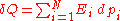
so that
The two above definitions of heat and work are among the few expressions of statistical mechanics
where the sum corresponding to the quantum case cannot be converted into an integral
in the classical limit of a microstate continuum
. The reason is that classical microstates are usually not defined in relation to a precise associated quantum microstate, which means that when work changes the energy associated to the energy levels of the system, the energy of classical microstates doesn't follow this change.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a microstate is a specific microscopic configuration of a thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
that the system may occupy with a certain probability in the course of its thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
.
A macrostate is characterized by a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of possible states across a certain statistical ensemble
Statistical ensemble (mathematical physics)
In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real...
of all microstates. This distribution describes the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of finding the system in a certain microstate. In the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
, the microstates visited by a macroscopic system during its fluctuations all have the same macroscopic properties.
Microscopic definitions of thermodynamic concepts
Statistical mechanics links the empirical thermodynamic properties of a system to the statistical distribution of an ensemble of microstates. All macroscopic thermodynamic properties of a system may be calculated from the partition function that sums the energy of all its microstates.At any moment a system is distributed across an ensemble of N microstates, each denoted by i, and having a probability of occupation pi, and an energy
 . These microstates form a discrete set as defined by quantum statistical mechanics
. These microstates form a discrete set as defined by quantum statistical mechanicsQuantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
, and
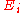 is an energy level
is an energy levelEnergy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
of the system.
Internal energy
The internal energy is the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the system's energy

This is a microscopic statement of the first law of thermodynamics
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
.
Entropy
The absolute entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
exclusively depends on the probabilities of the microstates and is defined as
where
 is Boltzmann's constant.
is Boltzmann's constant.Entropy is formulated by the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. The third law of thermodynamics
Third law of thermodynamics
The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
is consistent with this definition, since zero entropy means that the macrostate of the system reduces to a single microstate.
Heat and work
HeatHeat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
is the energy transfer associated with a disordered, microscopic action on the system, associated with jumps in energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s of the system.
Work
Work (thermodynamics)
In thermodynamics, work performed by a system is the energy transferred to another system that is measured by the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics. Thermodynamic work encompasses...
is the energy transfer associated to the effect of an ordered, macroscopic action on the system. If this action acts very slowly then the Adiabatic theorem
Adiabatic theorem
The adiabatic theorem is an important concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock , can be stated as follows:...
implies that this will not cause a jump in the energy level of the system. The internal energy of the system can only change due to a change of the energies of the system's energy levels.
The microscopic definitions of heat and work are the following:
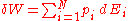
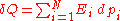
so that

The two above definitions of heat and work are among the few expressions of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
where the sum corresponding to the quantum case cannot be converted into an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
in the classical limit of a microstate continuum
Microstate continuum
A microstate continuum is the fluctuation spectrum of a thermodynamic system in the classical limit of high temperatures. Classical here is to be understood in opposition to quantum statistical mechanics.-See also:...
. The reason is that classical microstates are usually not defined in relation to a precise associated quantum microstate, which means that when work changes the energy associated to the energy levels of the system, the energy of classical microstates doesn't follow this change.
See also
- Quantum statistical mechanicsQuantum statistical mechanicsQuantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
- Degrees of freedom (physics and chemistry)Degrees of freedom (physics and chemistry)A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
- Ergodic hypothesisErgodic hypothesisIn physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
- Phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...


