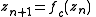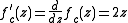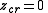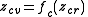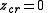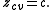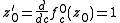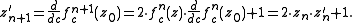Complex quadratic polynomial
Encyclopedia
A complex quadratic polynomial is a quadratic polynomial
whose coefficient
s are complex number
s.
), one can distinguish its 4 main forms:
The monic and centered form has the following properties:
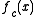is affine
conjugate
to the general form of the quadratic polynomial it is often used to study complex dynamics
and to create images of Mandelbrot
, Julia
and Fatou sets.
When one wants change from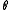
to 
:
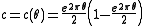
When one wants change from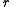
to 
:
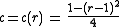
(here named doubling map) and the quadratic polynomial.
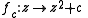parametrised by 
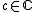is called :
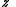and parameter
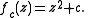
When it is used as an evolution function
of the discrete nonlinear dynamical system
:
it is named quadratic
map
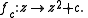
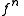denotes the n-th iteration of the function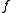 
not exponentiation
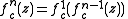
so
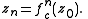
Because the above notation can have many meanings Milnor writes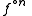
for nth iterate of function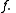 
of
is a point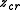 
in the dynamical plane such that the derivative
vanishes :
Since
implies
we see that the only (finite) critical point of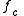
is the point 
.
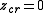It is an initial point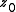
for Mandelbrot set
iteration.
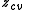of 
is the image of a critical point:
Since
we have
So the parameter
is the critical value of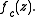 
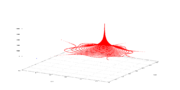Forward orbit
of a critical point is called a critical orbit. Critical orbits are very important because every attracting periodic orbit
attracts a critical point, so studying the critical orbits helps us understand the dynamics in the Fatou set.
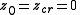
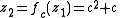
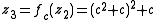
This orbit falls into an attracting periodic cycle
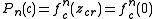
so
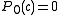
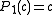
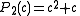
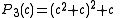
These polynomials are used for :
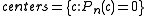
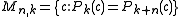
These curves create skeleton of bifurcation diagram
( the dark lines )
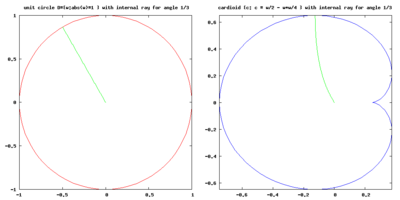One can use the Julia-Mandelbrot 4-dimensional space for a global analysis of this dynamical system.
In this space there are 2 basic types of 2-D planes :
There is also another plane used to analyze such dynamical systems w-plane :
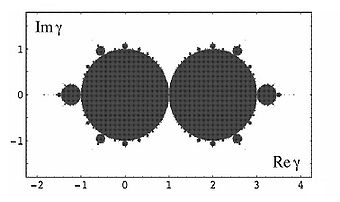The phase space
of a quadratic map is called its parameter plane. Here:
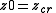is constant
and
is variable.
There is no dynamics here. It is only a set of parameter values. There are no orbits on the parameter plane.
The parameter plane consists of :
There are many different subtypes of the parameter plane
The dynamical plane consists of:
Here,
is a constant
and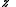
is a variable.
The two-dimensional dynamical plane can be treated as a Poincare cross-section
of three-dimensional space of continuous dynamical system.
The first derivative
of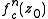
with respect to c is
This derivative
can be found by iteration
starting with
and then replacing at every consecutive step
This can easily be verified by using the chain rule
for the derivative.
This derivative is used in the distance estimation method for drawing a Mandelbrot set.
at a fixed point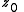
at a periodic point z0 of period p
It is used to check the stability
of periodic (also fixed) points
.
at nonperiodic point :
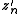
This derivative
can be found by iteration
starting with
and then :
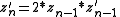
This dervative is used for computing external distance to Julia set.
(SD for short) of f is :
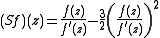
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
whose coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Forms
When the quadratic polynomial has only one variable ( univariateUnivariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
), one can distinguish its 4 main forms:
- The general form,
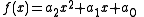. - The factored form used for logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
-
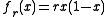
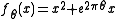which has an indifferent fixed point with multiplier 
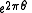at the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect... - The monic and centered form,
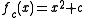
The monic and centered form has the following properties:
- It is the simplest form of a nonlinearNonlinearity (disambiguation)Nonlinear generally refers to a situation that has a disproportionate cause and effect.In science and mathematics, nonlinearity can refer to:* Nonlinear optics, in physics, examines the properties of light in media in which the polarization responds nonlinearly to the electric field.* Nonlinear...
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with one coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
(parameterParameterParameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
), - It is an unicritical polynomial, i.e. it has one critical pointCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
, - It is a centered polynomial (the sum of its critical points is zero),
- It can be postcritically finite, i.e. If the orbit of the critical point is finite. It is when critical point is periodic or preperiodic.
- It is a unimodal functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, - It is a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
, - It is an entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
.
Between forms
Since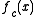 is affineAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
conjugate
Topological conjugation
In mathematics, two functions are said to be topologically conjugate to one another if there exists a homeomorphism that will conjugate the one into the other...
to the general form of the quadratic polynomial it is often used to study complex dynamics
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
and to create images of Mandelbrot
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
, Julia
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
and Fatou sets.
When one wants change from
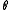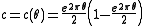
to : When one wants change from
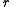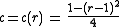
to :With doubling map
There is semi-conjugacy between the dyadic transformationDyadic transformation
The dyadic transformation is the mapping produced by the rule...
(here named doubling map) and the quadratic polynomial.
Family
The family of quadratic polynomials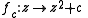 parametrised by 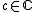is called :
- the Douady-Hubbard family of quadratic polynomials
- quadratic family
Map
The monic and centered form is typically used with variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
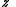and parameterParameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
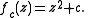
When it is used as an evolution function
Dynamical system (definition)
The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
of the discrete nonlinear dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
:
it is named quadratic
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
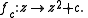
Notation
Here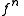 denotes the n-th iteration of the function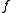 Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
not exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
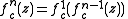
so
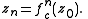
Because the above notation can have many meanings Milnor writes
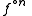for nth iterate of function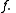 Critical point
A critical pointCritical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of
is a point 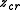in the dynamical plane such that the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
vanishes :
Since
implies
we see that the only (finite) critical point of
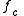is the point 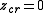.It is an initial point
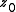for Mandelbrot setMandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
iteration.
Critical value
A critical valueCritical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
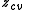of is the image of a critical point:
Since
we have
So the parameter
is the critical value of 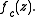Critical orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
of a critical point is called a critical orbit. Critical orbits are very important because every attracting periodic orbit
Periodic points of complex quadratic mappings
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
attracts a critical point, so studying the critical orbits helps us understand the dynamics in the Fatou set.
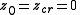
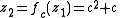
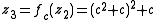
This orbit falls into an attracting periodic cycle
Periodic points of complex quadratic mappings
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
Critical sector
The critical sector is a sector of the dynamical plane containing the critical point .Critical polynomial
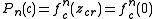
so
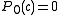
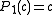
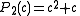
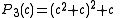
These polynomials are used for :
- finding centers of these Mandelbrot set components of period n. Centers are roots of n-th critical polynomials
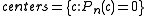
- finding roots of Mandelbrot set components of period n ( local minimum of
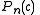) - Misiurewicz pointMisiurewicz pointA Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
s
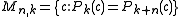
Critical curves
Diagrams of critical polynomials are called critical curves.These curves create skeleton of bifurcation diagram
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
( the dark lines )
Planes
In this space there are 2 basic types of 2-D planes :
- the dynamical ( dynamic ) plane,
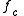-plane or c-plane - the parameter plane or z-plane.
There is also another plane used to analyze such dynamical systems w-plane :
- the conjugation plane
- model plane
Parameter plane
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of a quadratic map is called its parameter plane. Here:
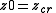is constantCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
and
is variable.There is no dynamics here. It is only a set of parameter values. There are no orbits on the parameter plane.
The parameter plane consists of :
- The Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
- The bifurcation locusBifurcation locusIn complex dynamics, the bifurcation locus of a family of holomorphic functions informally is a locus of those maps for which the dynamical behavior changes drastically under a small perturbation of the parameter. Thus the bifurcation locus can be thought of as an analog of the Julia set in...
= boundary of Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape... - Bounded hyperbolic components of the Mandelbrot set = interior of Mandelbrot set = Connectedness locusConnectedness locusIn one-dimensional complex dynamics, the connectedness locus in a parameter space of polynomials or rational functions consists of those parameters for which the corresponding Julia set is connected....
- The bifurcation locus
- The complement of the Mandelbrot set
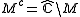= unbounded hyperbolic component
There are many different subtypes of the parameter plane
Dynamical plane
On the dynamical plane one can find:- The Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
- The Filled Julia setFilled Julia setThe filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
- The Fatou set
- Orbits .
The dynamical plane consists of:
- Fatou set
- Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
Here,
is a constantCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
and
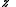is a variable.The two-dimensional dynamical plane can be treated as a Poincare cross-section
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
of three-dimensional space of continuous dynamical system.
Derivative with respect to c
On parameter plane :-
is a variable -
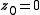is constant
The first derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
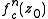with respect to c is
This derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
can be found by iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
starting with
and then replacing at every consecutive step
This can easily be verified by using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
for the derivative.
This derivative is used in the distance estimation method for drawing a Mandelbrot set.
Derivative with respect to z
On dynamical plane :-
is a variable -
is a constant
at a fixed point
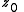
at a periodic point z0 of period p
It is used to check the stability
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
of periodic (also fixed) points
Periodic points of complex quadratic mappings
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
.
at nonperiodic point :
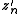
This derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
can be found by iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
starting with
and then :
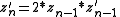
This dervative is used for computing external distance to Julia set.
Schwarzian derivative
The Schwarzian derivativeSchwarzian derivative
In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and...
(SD for short) of f is :
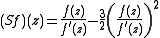
See also
- Misiurewicz pointMisiurewicz pointA Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
- Periodic points of complex quadratic mappingsPeriodic points of complex quadratic mappingsThis article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
- Mandelbrot setMandelbrot setThe Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
- Julia setJulia setIn the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
- Milnor–Thurston kneading theoryMilnor–Thurston kneading theoryThe Milnor–Thurston kneading theory is a mathematical theory which analyzes the iterates of piecewise monotone mappings of an interval into itself...