A map projection is any method of representing the surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

 of a sphere or other three-dimensional body on a plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

. Map projections are necessary for creating map

Map

A map is a visual representation of an area—a symbolic depiction highlighting relationships between elements of that space such as objects, regions, and themes....

s. All map projections distort the surface in some fashion. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. There is no limit to the number of possible map projections.

Background

For simplicity, this article usually assumes that the surface to be mapped is the surface of a sphere. However, the Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

 and other sufficiently large celestial bodies are generally better modeled as oblate spheroids, and small objects such as asteroid

Asteroid

Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...

s often have irregular shapes. These other surfaces can be mapped as well. Therefore, more generally, a map projection is any method of "flattening" into a plane a continuous surface having curvature in all three spatial dimensions.

Projection as used here is not limited to perspective

Perspective (graphical)

Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...

 projections, such as those resulting from casting a shadow on a screen, or the rectilinear image produced by a pinhole camera

Pinhole camera

A pinhole camera is a simple camera without a lens and with a single small aperture – effectively a light-proof box with a small hole in one side. Light from a scene passes through this single point and projects an inverted image on the opposite side of the box...

 on a flat film plate. Rather, any mathematical function transforming coordinates from the curved surface to the plane is a projection.

Carl Friedrich Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

's Theorema Egregium

Theorema Egregium

Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...

 proved that a sphere cannot be represented on a plane without distortion. Since any method of representing a sphere's surface on a plane is a map projection, all map projections distort. Every distinct map projection distorts in a distinct way. The study of map projections is the characterization of these distortions.

A map

Map

A map is a visual representation of an area—a symbolic depiction highlighting relationships between elements of that space such as objects, regions, and themes....

 of the Earth is a representation of a curved surface on a plane. Therefore a map projection must have been used to create the map, and, conversely, maps could not exist without map projections. Maps can be more useful than globe

Globe

A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...

s in many situations: they are more compact and easier to store; they readily accommodate an enormous range of scales; they are viewed easily on computer displays; they can facilitate measuring properties of the terrain being mapped; they can show larger portions of the Earth's surface at once; and they are cheaper to produce and transport. These useful traits of maps motivate the development of map projections.

Metric properties of maps

Many properties can be measured on the Earth's surface independently of its geography. Some of these properties are:

• Area
  Area
  Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
  
  
• Shape
  Shape
  The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
  
  
• Direction
  Direction (geometry, geography)
  Direction is the information contained in the relative position of one point with respect to another point without the distance information. Directions may be either relative to some indicated reference , or absolute according to some previously agreed upon frame of reference Direction is the...
  
  
• Bearing
  Bearing (navigation)
  In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
  
  
• Distance
  Distance
  Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
  
  
• Scale
  Scale (map)
  The scale of a map is defined as the ratio of a distance on the map to the corresponding distance on the ground.If the region of the map is small enough for the curvature of the Earth to be neglected, then the scale may be taken as a constant ratio over the whole map....
  
  

Map projections can be constructed to preserve one or more of these properties, though not all of them simultaneously. Each projection preserves or compromises or approximates basic metric properties in different ways. The purpose of the map determines which projection should form the base for the map. Because many purposes exist for maps, many projections have been created to suit those purposes.

Another consideration in the configuration of a projection is its compatibility with data sets to be used on the map. Data sets are geographic information; their collection depends on the chosen datum (model) of the Earth. Different datums assign slightly different coordinates to the same location, so in large scale maps, such as those from national mapping systems, it is important to match the datum to the projection. The slight differences in coordinate assignation between different datums is not a concern for world maps or other vast territories, where such differences get shrunk to imperceptibility.

Which projection is best?

Due to the many uses of maps and the vast range of scales at which they are created, no single map projection serves well for all purposes. Modern national mapping systems typically employ a transverse Mercator

Transverse Mercator projection

The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the UTM...

 or close variant for large-scale maps in order to preserve conformality

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

 and low variation in scale over small areas. But for smaller-scale maps, such as those spanning continents or the entire world, a plethora of projections are in common use according to their fitness for the purpose.

Thematic maps normally require an equal area projection so that phenomena per unit area are shown in correct proportion.
However, representing area ratios correctly necessarily distorts shapes more than many maps that are not equal-area. Hence reference maps of the world often appear on compromise projections instead. Due to the severe distortions inherent in any map of the world, within reason the choice of projection becomes largely one of æsthetics.

While the mathematics of projection do not allow any particular map projection to stand out as an unqualified "best", on the other hand, the literature singles out the Mercator projection

Mercator projection

The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...

 as having been overused and abused. The problem has long been recognized even outside professional circles: a 1943 New York Times editorial states:

Likewise, the Peters map controversy motivated the American Cartographic Association (now Cartography and Geographic Information Society) to produce a series of booklets (including Which Map is Best) designed to educate the public about map projections and distortion in maps. In 1989 and 1990, after some internal debate, seven North American geographic organizations adopted a resolution recommending against using any rectangular projection (including Mercator and Gall–Peters) for reference maps of the world.

Construction of a map projection

The creation of a map projection involves two steps:

1. Selection of a model for the shape of the Earth or planetary body (usually choosing between a sphere
   Sphere
   A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
   
    or ellipsoid). Because the Earth's actual shape is irregular, information is lost in this step.
2. Transformation of geographic coordinates (longitude
   Longitude
   Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
   
    and latitude
   Latitude
   In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
   
   ) to Cartesian
   Cartesian coordinate system
   A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
   
    (x,y) or polar
   Polar coordinate system
   In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
   
    plane coordinates. Cartesian coordinates normally have a simple relation to eastings and northings
   Easting and northing
   The terms easting and northing are geographic Cartesian coordinates for a point. Easting refers to the eastward-measured distance , while northing refers to the northward-measured distance...
   
    defined on a grid superimposed on the projection.

Some of the simplest map projections are literally projections, as obtained by placing
a light source at some definite point relative to the globe and projecting its features onto a specified surface. This is not the case for most projections which are defined only in terms of mathematical formulae that have no direct physical interpretation.

Choosing a projection surface

A surface that can be unfolded or unrolled into a plane or sheet without stretching, tearing or shrinking is called a developable surface

Developable surface

In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...

. The cylinder

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

, cone

Cone (geometry)

A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...

  and of course the plane are all developable surfaces. The sphere and ellipsoid are not developable surfaces. As noted in the introduction, any projection of a sphere (or an ellipsoid) onto a plane will have to distort the image. (To compare, one cannot flatten an orange peel without tearing or warping it.)

One way of describing a projection is first to project from the Earth's surface to a developable surface such as a cylinder or cone, and then to unroll the surface into a plane. While the first step inevitably distorts some properties of the globe, the developable surface can then be unfolded without further distortion.

Aspects of the projection

Once a choice is made between projecting onto a cylinder, cone, or plane, the aspect of the shape must be specified. The aspect describes how the developable surface is placed relative to the globe: it may be normal (such that the surface's axis of symmetry coincides with the Earth's axis), transverse (at right angles to the Earth's axis) or oblique (any angle in between). The developable surface may also be either tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

or secant

Secant line

A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...

to the sphere or ellipsoid. Tangent means the surface touches but does not slice through the globe; secant means the surface does slice through the globe. Insofar as preserving metric properties goes, it is never advantageous to move the developable surface away from contact with the globe, so that possibility is not discussed here.

Scale

A globe

Globe

A globe is a three-dimensional scale model of Earth or other spheroid celestial body such as a planet, star, or moon...

 is the only way to represent the earth with constant scale

Scale (map)

The scale of a map is defined as the ratio of a distance on the map to the corresponding distance on the ground.If the region of the map is small enough for the curvature of the Earth to be neglected, then the scale may be taken as a constant ratio over the whole map....

 throughout the entire map in all directions. A map cannot achieve that property for any area, no matter how small. It can, however, achieve constant scale along specific lines.

Some possible properties are:

• The scale depends on location, but not on direction. This is equivalent to preservation of angles, the defining characteristic of a conformal map
  Conformal map
  In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
  
  .
• Scale is constant along any parallel in the direction of the parallel. This applies for any cylindrical or pseudocylindrical projection in normal aspect.
• Combination of the above: the scale depends on latitude only, not on longitude or direction. This applies for the Mercator projection
  Mercator projection
  The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
  
   in normal aspect.
• Scale is constant along all straight lines radiating from a particular geographic location. This is the defining characteristic of an equidistant projection such as the Azimuthal equidistant projection
  Azimuthal equidistant projection
  The azimuthal equidistant projection is a type of map projection.A useful application for this type of projection is a polar projection in which all distances measured from the center of the map along any longitudinal line are accurate; an example of a polar azimuthal equidistant projection can be...
  
  . There are also projections (Maurer, Close) where true distances from two points are preserved.

Choosing a model for the shape of the Earth

Projection construction is also affected by how the shape of the Earth is approximated. In the following discussion on projection categories, a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 is assumed. However, the Earth is not exactly spherical but is closer in shape to an oblate ellipsoid, a shape which bulges around the equator

Equator

An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....

. Selecting a model for a shape of the Earth involves choosing between the advantages and disadvantages of a sphere versus an ellipsoid. Spherical models are useful for small-scale maps such as world atlases and globes, since the error at that scale is not usually noticeable or important enough to justify using the more complicated ellipsoid. The ellipsoidal model is commonly used to construct topographic map

Topographic map

A topographic map is a type of map characterized by large-scale detail and quantitative representation of relief, usually using contour lines in modern mapping, but historically using a variety of methods. Traditional definitions require a topographic map to show both natural and man-made features...

s and for other large- and medium-scale maps that need to accurately depict the land surface.

A third model of the shape of the Earth is the geoid

Geoid

The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...

, a complex and more accurate representation of the global mean sea level surface that is obtained through a combination of terrestrial and satellite gravity measurements. This model is not used for mapping, because of its complexity, but is used for control purposes in the construction of geographic datums. (In geodesy, plural of "datum" is "datums" rather than "data".) A geoid is used to construct a datum by adding irregularities to the ellipsoid in order to better match the Earth's actual shape. It takes into account the large-scale features in the Earth's gravity field associated with mantle convection

Mantle convection

Mantle convection is the slow creeping motion of Earth's rocky mantle caused by convection currents carrying heat from the interior of the Earth to the surface. The Earth's surface lithosphere, which rides atop the asthenosphere , is divided into a number of plates that are continuously being...

 patterns, and the gravity signatures of very large geomorphic features such as mountain ranges, plateaus and plains. Historically, datums have been based on ellipsoids that best represent the geoid within the region that the datum is intended to map. Each ellipsoid has a distinct major and minor axis. Different controls (modifications) are added to the ellipsoid in order to construct the datum, which is specialized for a specific geographic region (such as the North American Datum

North American Datum

The North American Datum is the official datum used for the primary geodetic network in North America.In the fields of cartography and land-use there are currently two North American Datums in use: the North American Datum of 1927 and the North American Datum of 1983...

). A few modern datums, such as WGS84 which is used in the Global Positioning System

Global Positioning System

The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...

, are optimized to represent the entire earth as well as possible with a single ellipsoid, at the expense of accuracy in smaller regions.

Classification

A fundamental projection classification is based on the type of projection surface onto which the globe is conceptually projected. The projections are described in terms of placing a gigantic surface in contact with the earth, followed by an implied scaling operation. These surfaces are cylindrical (e.g. Mercator

Mercator projection

The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...

), conic (e.g., Albers

Albers projection

The Albers equal-area conic projection, or Albers projection , is a conic, equal areamap projection that uses two standard parallels. Although scale and shape are not preserved, distortion is minimal between the standard parallels.The Albers projection is the standard projection for British Columbia...

), or azimuthal or plane (e.g. stereographic

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

). Many mathematical projections, however, do not neatly fit into any of these three conceptual projection methods. Hence other peer categories have been described in the literature, such as pseudoconic, pseudocylindrical, pseudoazimuthal, retroazimuthal, and polyconic

Polyconic projection

Polyconic can refer either to a class of map projections or to a specific projection known less ambiguously as the American Polyconic. Polyconic as a class refers to those projections whose parallels are all non-concentric circular arcs, except for a straight equator, and the centers of these...

.

Another way to classify projections is according to properties of the model they preserve. Some of the more common categories are:

• Preserving direction (azimuthal), a trait possible only from one or two points to every other point
• Preserving shape locally (conformal or orthomorphic)
• Preserving area (equal-area or equiareal or equivalent or authalic)
• Preserving distance (equidistant), a trait possible only between one or two points and every other point
• Preserving shortest route, a trait preserved only by the gnomonic projection
  Gnomonic projection
  A gnomonic map projection displays all great circles as straight lines. Thus the shortest route between two locations in reality corresponds to that on the map. This is achieved by projecting, with respect to the center of the Earth , the Earth's surface onto a tangent plane. The least distortion...
  
  

NOTE: Because the sphere is not a developable surface, it is impossible to construct a map projection that is both equal-area and conformal.

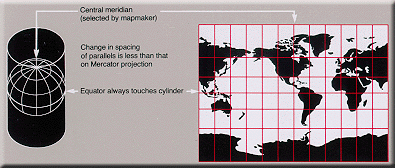
Cylindrical

See also: List of map projections#Cylindrical.

‎ The term "normal cylindrical projection" is used to refer to any projection in which meridians

Meridian (geography)

A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...

 are mapped to equally spaced vertical lines and circles of latitude (parallels) are mapped to horizontal lines.

The mapping of meridians to vertical lines can be visualized by imagining a cylinder (of which the axis coincides with the Earth's axis of rotation) wrapped around the Earth and then projecting onto the cylinder, and subsequently unfolding the cylinder.

By the geometry of their construction, cylindrical projections stretch distances east-west. The amount of stretch is the same at any chosen latitude on all cylindrical projections, and is given by the secant

Trigonometric function

In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...

 of the latitude

Latitude

In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...

 as a multiple of the equator's scale. The various cylindrical projections are distinguished from each other solely by their north-south stretching (where latitude is given by φ):

• North-south stretching is equal to the east-west stretching (secant φ): The east-west scale matches the north-south scale: conformal cylindrical or Mercator
  Mercator projection
  The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
  
  ; this distorts areas excessively in high latitudes (see also transverse Mercator
  Transverse Mercator projection
  The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the UTM...
  
  ).
• North-south stretching growing rapidly with latitude, even faster than east-west stretching (secant² φ: The cylindric perspective (= central cylindrical) projection; unsuitable because distortion is even worse than in the Mercator projection.
• North-south stretching grows with latitude, but less quickly than the east-west stretching: such as the Miller cylindrical projection
  Miller cylindrical projection
  thumb|450px|The Miller cylindrical projection is a modified Mercator projection, proposed by Osborn Maitland Miller in 1942. The latitude is scaled by a factor of 4/5, projected according to Mercator, and then the result is multiplied by 5/4 to retain scale along the equator...
  
   (secant[4φ/5]).
• North-south distances neither stretched nor compressed (1): equidistant cylindrical or plate carrée.
• North-south compression precisely the reciprocal of east-west stretching (cosine φ): equal-area cylindrical
  Cylindrical equal-area projection
  In cartography, the cylindrical equal-area projection is a family of cylindrical, equal area map projections.-Cylindrical projections:The term "normal cylindrical projection" is used to refer to any projection in which meridians are mapped to equally spaced vertical lines and circles of latitude ...
  
   (with many named specializations such as Gall–Peters or Gall orthographic, Behrmann
  Behrmann projection
  The Behrmann projection is a cylindrical map projection. This is an orthographic projection onto a cylinder secant at the 30° parallels. It is equal-area, but distortion of shape increases with distance from the standard parallels. Scale is true along the standard parallels and constant between two...
  
  , and Lambert cylindrical equal-area
  Lambert cylindrical equal-area projection
  In cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is acylindrical, equal area map projection...
  
  ). This divides north-south distances by a factor equal to the secant of the latitude, preserving area but heavily distorting shapes.

In the first case (Mercator), the east-west scale always equals the north-south scale. In the second case (central cylindrical), the north-south scale exceeds the east-west scale everywhere away from the equator. Each remaining case has a pair of identical latitudes of opposite sign (or else the equator) at which the east-west scale matches the north-south-scale.

Normal cylindrical projections map the whole Earth as a finite rectangle, except in the first two cases, where the rectangle stretches infinitely tall while retaining constant width.

Pseudocylindrical

Pseudocylindrical projections represent the central meridian

Meridian (geography)

A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...

 and each parallel

Circle of latitude

A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...

 as a single straight line segment, but not the other meridians. Each pseudocylindrical projection represents a point on the Earth along the straight line representing its parallel, at a distance which is a function of its difference in longitude from the central meridian.

• Sinusoidal
  Sinusoidal projection
  The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, appearing in a world map of 1570...
  
  : the north-south scale and the east-west scale are the same throughout the map, creating an equal-area map. On the map, as in reality, the length of each parallel is proportional to the cosine of the latitude. Thus the shape of the map for the whole earth is the region between two symmetric rotated cosine curves.

The true distance between two points on the same meridian corresponds to the distance on the map between the two parallels, which is smaller than the distance between the two points on the map. The true distance between two points on the same parallel—and the true area of shapes on the map—are not distorted. The meridians drawn on the map help the user to realize the shape distortion and mentally compensate for it.

• Collignon projection
  Collignon projection
  The Collignon projection is an equal-area pseudocylindrical map projection first known to be published by Édouard Collignon in 1865 and subsequently cited by A...
  
  , which in its most common forms represents each meridian as 2 straight line segments, one from each pole to the equator.
• Mollweide
  Mollweide projection
  The Mollweide projection is a pseudocylindrical map projection generally used for global maps of the world . Also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection...
  
  
• Goode homolosine
  Goode homolosine projection
  The Goode homolosine projection is pseudocylindrical, equal-area, composite map projection used for world maps. Normally it is presented with multiple interruptions...
  
  
• Eckert IV

• Eckert VI

• Kavrayskiy VII
  Kavrayskiy VII projection
  The Kavrayskiy VII projection is a map projection invented by Vladimir V. Kavrayskiy in 1939 for use as a general purpose pseudocylindrical projection. Like the Robinson projection, it is a compromise intended to produce good quality maps with low distortion overall...
  
  
• Tobler hyperelliptical
  Tobler hyperelliptical projection
  The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections used for mapping the earth. It is named for Waldo R...
  
  

Hybrid

The HEALPix

HEALPix

HEALPix , an acronym for Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere, can refer to either an algorithm for pixelisation of the 2-sphere, an associated software package, or an associated class of map projections.The HEALPix projection is a general class of spherical projections,...

 projection combines an equal-area cylindrical projection in equatorial regions with the Collignon projection

Collignon projection

The Collignon projection is an equal-area pseudocylindrical map projection first known to be published by Édouard Collignon in 1865 and subsequently cited by A...

 in polar areas.

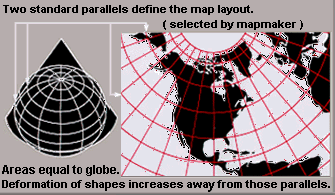
Conical

• Equidistant conic
• Lambert conformal conic
  Lambert conformal conic projection
  A Lambert conformal conic projection is a conic map projection, which is often used for aeronautical charts. In essence, the projection superimposes a cone over the sphere of the Earth, with two reference parallels secant to the globe and intersecting it. This minimizes distortion from projecting...
  
  
• Albers conic

Pseudoconical

• Bonne
  Bonne projection
  A Bonne projection is a pseudoconical equal-area map projection, sometimes called a dépôt de la guerre or a Sylvanus projection. Although named after Rigobert Bonne , the projection was in use prior to his birth, in 1511 by Sylvano, Honter in 1561, De l'Isle before 1700 and Coronelli in 1696.The...
  
  
• Werner cordiform, upon which distances are correct from one pole, as well as along all parallels.
• Continuous American polyconic
  Polyconic projection
  Polyconic can refer either to a class of map projections or to a specific projection known less ambiguously as the American Polyconic. Polyconic as a class refers to those projections whose parallels are all non-concentric circular arcs, except for a straight equator, and the centers of these...
  
  

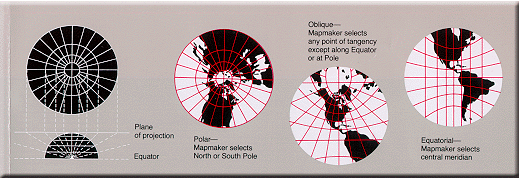
Azimuthal (projections onto a plane)

Azimuthal projections have the property that directions from a central point are preserved (and hence, great circle

Great circle

A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...

s through the central point are represented by straight lines on the map). Usually these projections also have radial symmetry in the scales and hence in the distortions: map distances from the central point are computed by a function r(d) of the true distance d, independent of the angle; correspondingly, circles with the central point as center are mapped into circles which have as center the central point on the map.

The mapping of radial lines can be visualized by imagining a plane tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 to the Earth, with the central point as tangent point.

The radial scale is r'(d) and the transverse scale r(d)/(R sin(d/R)) where R is the radius of the Earth.

Some azimuthal projections are true perspective projections; that is, they can be constructed mechanically, projecting the surface of the Earth by extending lines from a point of perspective (along an infinite line through the tangent point and the tangent point's antipode

Antipodal point

In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

) onto the plane:

• The gnomonic projection
  Gnomonic projection
  A gnomonic map projection displays all great circles as straight lines. Thus the shortest route between two locations in reality corresponds to that on the map. This is achieved by projecting, with respect to the center of the Earth , the Earth's surface onto a tangent plane. The least distortion...
  
   displays great circle
  Great circle
  A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
  
  s as straight lines. Can be constructed by using a point of perspective at the center of the Earth. r(d) = c tan(d/R); a hemisphere already requires an infinite map,
• The General Perspective Projection
  General Perspective projection
  The General Perspective Projection is a map projection of cartography.When the Earth is photographed from space, the camera records the view as a perspective projection. If the camera precisely faces the center of the Earth, the projection is Vertical Perspective...
  
   can be constructed by using a point of perspective outside the earth. Photographs of Earth (such as those from the International Space Station
  International Space Station
  The International Space Station is a habitable, artificial satellite in low Earth orbit. The ISS follows the Salyut, Almaz, Cosmos, Skylab, and Mir space stations, as the 11th space station launched, not including the Genesis I and II prototypes...
  
  ) give this perspective.
• The orthographic projection
  Orthographic projection (cartography)
  An orthographic projection is a map projection of cartography. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection, in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic...
  
   maps each point on the earth to the closest point on the plane. Can be constructed from a point of perspective an infinite distance from the tangent point; r(d) = c sin(d/R). Can display up to a hemisphere on a finite circle. Photographs of Earth from far enough away, such as the Moon
  Moon
  The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
  
  , give this perspective.
• The azimuthal conformal projection, also known as the stereographic projection
  Stereographic projection
  The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
  
  , can be constructed by using the tangent point's antipode
  Antipodal point
  In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
  
   as the point of perspective. r(d) = c tan(d/2R); the scale is c/(2R cos²(d/2R)). Can display nearly the entire sphere on a finite circle. The full sphere requires an infinite map.

Other azimuthal projections are not true perspective

Perspective (graphical)

Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...

 projections:

• Azimuthal equidistant
  Azimuthal equidistant projection
  The azimuthal equidistant projection is a type of map projection.A useful application for this type of projection is a polar projection in which all distances measured from the center of the map along any longitudinal line are accurate; an example of a polar azimuthal equidistant projection can be...
  
  : r(d) = cd; it is used by amateur radio
  Amateur radio
  Amateur radio is the use of designated radio frequency spectrum for purposes of private recreation, non-commercial exchange of messages, wireless experimentation, self-training, and emergency communication...
  
   operators to know the direction to point their antennas toward a point and see the distance to it. Distance from the tangent point on the map is proportional to surface distance on the earth ' onMouseout='HidePop("64988")' href="/topics/Flag_of_the_United_Nations">flag of the United Nations
  Flag of the United Nations
  The flag of the United Nations was adopted on October 20, 1947, and consists of the official emblem of the United Nations in white on a blue background. The emblem's design is described as:...
  
  )
• Lambert azimuthal equal-area
  Lambert azimuthal equal-area projection
  The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk . It accurately represents area in all regions of the sphere, but it does not accurately represent angles...
  
  . Distance from the tangent point on the map is proportional to straight-line distance through the earth: r(d) = c sin(d/2R)
• Logarithmic azimuthal is constructed so that each point's distance from the center of the map is the logarithm of its distance from the tangent point on the Earth. r(d) = c ln(d/d₀); locations closer than at a distance equal to the constant d₀ are not shown

Projections by preservation of a metric property

Conformal

Conformal map

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

 projections preserve angles locally. These are some conformal projections:

• Mercator
  Mercator projection
  The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
  
   – rhumb lines are represented by straight segments
• Transverse Mercator
  Transverse Mercator projection
  The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the UTM...
  
  
• Stereographic
  Stereographic projection
  The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
  
   - shape of circles is conserved
• Roussilhe
  Roussilhe oblique stereographic projection
  The Roussilhe oblique stereographic projection is a mapping projection developed by Henri Roussilhe in 1922. The projection uses a truncated series to approximate an oblique stereographic projection for the ellipsoid...
  
  
• Lambert conformal conic
  Lambert conformal conic projection
  A Lambert conformal conic projection is a conic map projection, which is often used for aeronautical charts. In essence, the projection superimposes a cone over the sphere of the Earth, with two reference parallels secant to the globe and intersecting it. This minimizes distortion from projecting...
  
  
• Peirce quincuncial projection
  Peirce quincuncial projection
  The Peirce quincuncial projection is a conformal map projection that presents the sphere as a square...
  
  
• Adams hemisphere-in-a-square projection
  Adams hemisphere-in-a-square projection
  The Adams-hemisphere-in-a-square is a conformal map projection for a hemisphere . It is a transverse version of the Peirce quincuncial projection. When it is used to represent the entire sphere it is known as the Adams doubly periodic projection....
  
  
• Guyou hemisphere-in-a-square projection
  Guyou hemisphere-in-a-square projection
  The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere . It is an oblique aspect of the Peirce quincuncial projection...
  
  

Equal-area

These are some projections that preserve area:

Equidistant

These are some projections that preserve distance from some standard point or line:

• Equirectangular
  Equirectangular projection
  The equirectangular projection is a very simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100...
  
  —distances along meridians are conserved
• Plate carrée—an Equirectangular projection
  Equirectangular projection
  The equirectangular projection is a very simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100...
  
   centered at the equator
• Azimuthal equidistant
  Azimuthal equidistant projection
  The azimuthal equidistant projection is a type of map projection.A useful application for this type of projection is a polar projection in which all distances measured from the center of the map along any longitudinal line are accurate; an example of a polar azimuthal equidistant projection can be...
  
  —distances along great circles radiating from centre are conserved
• Equidistant conic
• Sinusoidal
  Sinusoidal projection
  The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, appearing in a world map of 1570...
  
  —distances along parallels are conserved
• Werner cordiform distances from the North Pole
  North Pole
  The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
  
   are correct as are the curved distance on parallels
• Soldner
• Two-point equidistant
  Two-point equidistant projection
  The two-point equidistant projection is a map projection first described by Hans Maurer in 1919. Distances from any point on the map to two control points scale to the geodesic distances of the same points on the sphere. The projection is commonly used in National Geographic Society atlases for...
  
  : two "control points" are arbitrarily chosen by the map maker. Distance from any point on the map to each control point is proportional to surface distance on the earth.

Gnomonic

Great circle

Great circle

A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...

s are displayed as straight lines:

• Gnomonic projection
  Gnomonic projection
  A gnomonic map projection displays all great circles as straight lines. Thus the shortest route between two locations in reality corresponds to that on the map. This is achieved by projecting, with respect to the center of the Earth , the Earth's surface onto a tangent plane. The least distortion...
  
  

Retroazimuthal

Direction to a fixed location B (the bearing at the starting location A of the shortest route) corresponds to the direction on the map from A to B:

• Littrow
  Littrow projection
  The Littrow projection is the only conformal retroazimuthal map projection. A retroazimuthal projection is one in which the direction to a fixed location B corresponds to the direction on the map from A to B.The Littrow projection allows direct measurement of the azimuth from any point on the...
  
  —the only conformal retroazimuthal projection
• Hammer retroazimuthal—also preserves distance from the central point
• Craig retroazimuthal
  Craig retroazimuthal projection
  The Craig retroazimuthal map projection was created by James Ireland Craig in 1909. It is a cylindrical projection preserving the direction from any place to another, predetermined place while avoiding some of the bizarre distortion of the Hammer retroazimuthal projection...
  
   aka Mecca or Qibla—also has vertical meridians

Compromise projections

Compromise projections give up the idea of perfectly preserving metric properties, seeking instead to strike a balance between distortions, or to simply make things "look right". Most of these types of projections distort shape in the polar regions more than at the equator. These are some compromise projections:

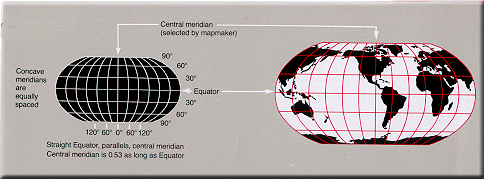
• Robinson
  Robinson projection
  The Robinson projection is a map projection of a world map, which shows the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image....
  
  
• van der Grinten
  Van der Grinten projection
  The van der Grinten projection is a compromise map projection that is neither equal-area nor conformal. It projects the entire Earth into a circle, though the polar regions are subject to extreme distortion. The projection was the first of four proposed by Alphons J. van der Grinten in 1904, and,...
  
  
• Miller cylindrical
  Miller cylindrical projection
  thumb|450px|The Miller cylindrical projection is a modified Mercator projection, proposed by Osborn Maitland Miller in 1942. The latitude is scaled by a factor of 4/5, projected according to Mercator, and then the result is multiplied by 5/4 to retain scale along the equator...
  
  
• Winkel Tripel
  Winkel tripel projection
  The Winkel Tripel projection , a modified azimuthal map projection, is one of three projections proposed by Oswald Winkel in 1921...
  
  
• Buckminster Fuller's Dymaxion
• B.J.S. Cahill's Butterfly Map
  Bernard J.S. Cahill
  B.J.S. Cahill , cartographer and architect, was the inventor of the octahedral "Butterfly Map" ; an early proponent of the San Francisco Civic Center ; and designer of the Columbarium of San Francisco.His Butterfly World Map, like Buckminster Fuller's later Dymaxion Map of 1943 and 1954, enabled all...
  
  
• Kavrayskiy VII
• Wagner VI
• Chamberlin trimetric
  Chamberlin trimetric projection
  The Chamberlin trimetric projection is a map projection where three points are fixed on the globe and the points on the sphere are mapped onto a plane by triangulation...
  
  
• Oronce Fine
  Oronce Finé
  Oronce Fine was a French mathematician and cartographer.-Life:...
  
  's cordiform

External links

• A Cornucopia of Map Projections, a visualization of distortion on a vast array of map projections in a single image.
• G.Projector, free software by can render many projections (NASA
  NASA
  The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
  
   GISS).
• Color images of map projections and distortion (Mapthematics.com).
• Geometric aspects of mapping: map projection (KartoWeb.itc.nl).
• Java world map projections, Henry Bottomley (BTInternet).
• Map projections http://www.3dsoftware.com/Cartography/USGS/MapProjections/, archived by the Wayback Machine
  Wayback Machine
  The Wayback Machine is a digital time capsule created by the Internet Archive non-profit organization, based in San Francisco, California. It is maintained with content from Alexa Internet. The service enables users to see archived versions of web pages across time, which the Archive calls a "three...
  
   (3DSoftware).
• Map projections, John Savard.
• Map Projections (MathWorld).
• Map Projections An interactive JAVA applet to study deformations (area, distance and angle) of map projections (UFF.br).
• Map Projections: How Projections Work (Progonos.com).
• Map Projections Poster (U.S. Geographical Survey).
• MapRef: The Internet Collection of MapProjections and Reference Systems in Europe
• PROJ.4 - Cartographic Projections Library.
• Projection Reference Table of examples and properties of all common projections (RadicalCartography.net)., Melita Kennedy (ESRI
  ESRI
  Esri is a software development and services company providing Geographic Information System software and geodatabase management applications. The headquarters of Esri is in Redlands, California....
  
  ).
• World Map Projections, Stephen Wolfram
  Stephen Wolfram
  Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
  
   based on work by Yu-Sung Chang (Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  ).