
Ordered ring
Encyclopedia
In abstract algebra
, an ordered ring is a commutative ring
 with a total order
with a total order
≤ such that for all a, b, and c in R:
Ordered rings are familiar from arithmetic
. Examples include the real number
s. (The rationals and reals in fact form ordered field
s.) The complex number
s do not form an ordered ring (or ordered field).
In analogy with real numbers, we call an element c ≠ 0, of an ordered ring positive if 0 ≤ c and negative if c ≤ 0. The set of positive (or, in some cases, nonnegative) elements in the ring R is often denoted by R+.
If a is an element of an ordered ring R, then the absolute value
of a, denoted |a|, is defined thus:
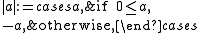
where -a is the additive inverse
of a and 0 is the additive identity element
.
A discrete ordered ring or discretely ordered ring is an ordered ring in which there is no element between 0 and 1. The integers are a discrete ordered ring, but the rational numbers are not.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an ordered ring is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
 with a total order
with a total orderTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
≤ such that for all a, b, and c in R:
- if a ≤ b then a + c ≤ b + c.
- if 0 ≤ a and 0 ≤ b then 0 ≤ ab.
Ordered rings are familiar from arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. Examples include the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. (The rationals and reals in fact form ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s.) The complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s do not form an ordered ring (or ordered field).
In analogy with real numbers, we call an element c ≠ 0, of an ordered ring positive if 0 ≤ c and negative if c ≤ 0. The set of positive (or, in some cases, nonnegative) elements in the ring R is often denoted by R+.
If a is an element of an ordered ring R, then the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a, denoted |a|, is defined thus:
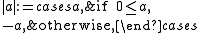
where -a is the additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of a and 0 is the additive identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
A discrete ordered ring or discretely ordered ring is an ordered ring in which there is no element between 0 and 1. The integers are a discrete ordered ring, but the rational numbers are not.
Basic properties
For all a, b and c in R:- If a ≤ b and 0 ≤ c, then ac ≤ bc. This property is sometimes used to define ordered rings instead of the second property in the definition above.
- |ab| = |a| |b|.
- An ordered ring that is not trivial is infinite.
- Exactly one of the following is true: a is positive, -a is positive, or a = 0. This property follows from the fact that ordered rings are abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, linearly ordered groupLinearly ordered groupIn abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
s with respect to addition. - An ordered ring R has no zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s if and only if the positive ring elements are closedClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under multiplication (i.e. if a and b are positive, then so is ab). - In an ordered ring, no negative element is a square. This is because if a ≠ 0 and a = b2 then b ≠ 0 and a = (-b )2; as either b or -b is positive, a must be positive.

