
Convex combination
Encyclopedia
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
, a convex combination is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
(which can be vectors, scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, or more generally points in an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
) where all coefficients are non-negative and sum up to 1.
More formally, given a finite number of points
 in a real vector space, a convex combination of these points is a point of the form
in a real vector space, a convex combination of these points is a point of the form
where the real numbers
 satisfy
satisfy  and
and 
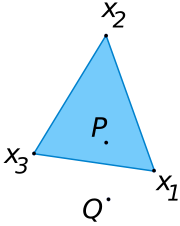
As a particular example, every convex combination of two points lies on the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
between the points.
All convex combinations are within the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the given points. In fact, the collection of all such convex combinations of points in the set constitutes the convex hull of the set.
There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval
 is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distribution
is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).
Other objects
- A convex combination of probability distributions is similarly a weighted sum (where
 satisfy the same constraints as above) of its component probability distributions, with probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
satisfy the same constraints as above) of its component probability distributions, with probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
:

Related constructions
- A conical combinationConical combinationGiven a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
is a linear combination with nonnegative coefficients - Weighted meanWeighted meanThe weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
s are functionally the same as convex combinations, but they use a different notation. The coefficients (weightsWeight functionA weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
) in a weighted mean are not required to sum to 1; instead the sum is explicitly divided from the linear combination. - Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
See also
- Affine hullAffine hullIn mathematics, the affine hull of a set S in Euclidean space Rn is the smallest affine set containing S, or equivalently, the intersection of all affine sets containing S...
- Carathéodory's theorem (convex hull)Carathéodory's theorem (convex hull)In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
- Convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

