
Dirichlet energy
Encyclopedia
In mathematics
, the Dirichlet's energy is a numerical measure of how variable a function
is. More abstractly, it is a quadratic
functional
on the Sobolev space
. The Dirichlet energy is intimately connected to Laplace's equation
and is named after the German
mathematician
Lejeune Dirichlet.
and function the Dirichlet's energy of the function is the real number
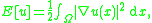
where denotes the gradient
vector field
of the function .
Solving Laplace's equation

(subject to appropriate boundary conditions) is equivalent to solving the variational problem
of finding a function that satisfies the boundary conditions and has minimal Dirichlet energy.
Such a solution is called a harmonic function
and such solutions are the topic of study in potential theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Dirichlet's energy is a numerical measure of how variable a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is. More abstractly, it is a quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
on the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
. The Dirichlet energy is intimately connected to Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
and is named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Lejeune Dirichlet.
Definition
Given an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and function the Dirichlet's energy of the function is the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
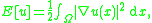
where denotes the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
of the function .
Properties and applications
Since it is the integral of a non-negative quantity, the Dirichlet's energy is itself non-negative, i.e. E[u] ≥ 0 for every function .Solving Laplace's equation

(subject to appropriate boundary conditions) is equivalent to solving the variational problem
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
of finding a function that satisfies the boundary conditions and has minimal Dirichlet energy.
Such a solution is called a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
and such solutions are the topic of study in potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
See also
- Dirichlet's principle
- Total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
- OscillationBounded mean oscillationIn harmonic analysis, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded...

