
Discrete exterior calculus
Encyclopedia
In mathematics
, the discrete exterior calculus (DEC) is the extension of the exterior calculus
to discrete
spaces including graphs
and finite element meshes
. DEC methods have proved to be very powerful in improving and analyzing finite element methods: for instance, DEC-based methods allow the use of highly non-uniform meshes to obtain accurate results. Non-uniform meshes are advantageous because they allow the use of large elements where the process to be simulated is relatively simple, as opposed to a fine resolution where the process may be complicated (e.g., near an obstruction to a fluid flow), while using less computational power than if a uniformly fine mesh were used.
relates the integral
of a differential (n − 1)-form
ω over the boundary
∂M of an n-dimension
al manifold M to the integral of dω (the exterior derivative
of ω, and a differential n-form on M) over M itself:
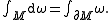
One could think of differential k-forms as linear operators that act on k-dimensional "bits" of space, in which case one might prefer to use the bra-ket notation
for a dual pairing. In this notation, Stokes' theorem reads as
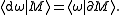
In finite element analysis, the first stage is often the approximation of the domain of interest by a triangulation
, T. For example, a curve would be approximated as a union of straight line segments; a surface would be approximated by a union of triangles, whose edges are straight line segments, which themselves terminate in points. Topologists would refer to such a construction as a simplicial complex
. The boundary operator on this triangulation/simplicial complex T is defined in the usual way: for example, if L is a directed line segment from one point, a, to another, b, then the boundary ∂L of L is the formal difference b − a.
A k-form on T is a linear operator acting on k-dimensional subcomplexes of T; e.g., a 0-form assigns values to points, and extends linearly to linear combinations of points; a 1-form assigns values to line segments in a similarly linear way. If S is a (k + 1)-dimensional subcomplex of T and ω is a k-form on T, then the discrete exterior derivative dω of ω is the unique (k + 1)-form defined so that Stokes' theorem holds:

Other concepts such as the discrete wedge product and the discrete Hodge star can also be defined.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the discrete exterior calculus (DEC) is the extension of the exterior calculus
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
to discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
spaces including graphs
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
and finite element meshes
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
. DEC methods have proved to be very powerful in improving and analyzing finite element methods: for instance, DEC-based methods allow the use of highly non-uniform meshes to obtain accurate results. Non-uniform meshes are advantageous because they allow the use of large elements where the process to be simulated is relatively simple, as opposed to a fine resolution where the process may be complicated (e.g., near an obstruction to a fluid flow), while using less computational power than if a uniformly fine mesh were used.
The discrete exterior derivative
Stokes' theoremStokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
relates the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a differential (n − 1)-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
ω over the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
∂M of an n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al manifold M to the integral of dω (the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of ω, and a differential n-form on M) over M itself:
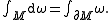
One could think of differential k-forms as linear operators that act on k-dimensional "bits" of space, in which case one might prefer to use the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
for a dual pairing. In this notation, Stokes' theorem reads as
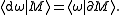
In finite element analysis, the first stage is often the approximation of the domain of interest by a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
, T. For example, a curve would be approximated as a union of straight line segments; a surface would be approximated by a union of triangles, whose edges are straight line segments, which themselves terminate in points. Topologists would refer to such a construction as a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. The boundary operator on this triangulation/simplicial complex T is defined in the usual way: for example, if L is a directed line segment from one point, a, to another, b, then the boundary ∂L of L is the formal difference b − a.
A k-form on T is a linear operator acting on k-dimensional subcomplexes of T; e.g., a 0-form assigns values to points, and extends linearly to linear combinations of points; a 1-form assigns values to line segments in a similarly linear way. If S is a (k + 1)-dimensional subcomplex of T and ω is a k-form on T, then the discrete exterior derivative dω of ω is the unique (k + 1)-form defined so that Stokes' theorem holds:

Other concepts such as the discrete wedge product and the discrete Hodge star can also be defined.
See also
- Discrete differential geometryDiscrete differential geometryDiscrete differential geometry is the study of discrete counterparts of notions in differential geometry. Instead of smooth curves and surfaces, there are polygons, meshes, and simplicial complexes...
- Discrete Morse theory
- Topological combinatoricsTopological combinatoricsThe discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....

