Unit sphere - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a unit sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

is the set of points of distance

Distance

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

is the set of points of distance

Distance

less than or equal to 1 from a fixed central point. Usually a specific point has been distinguished as the origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

of the space under study and it is understood that a unit sphere or unit ball is centered at that point. Therefore one speaks of "the" unit ball or "the" unit sphere.

For example, a one-dimensional sphere is the surface of what is commonly called a "circle", while such a circle's interior and surface together are the two-dimensional ball. Similarly, a two-dimensional sphere is the surface of the Euclidean solid known colloquially as a "sphere", while the interior and surface together are the three-dimensional ball.

A unit sphere is simply a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

of radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

one. The importance of the unit sphere is that any sphere can be transformed to a unit sphere by a combination of translation

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

and scaling

Scaling (geometry)

In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...

. In this way the properties of spheres in general can be reduced to the study of the unit sphere.

Unit spheres and balls in Euclidean space

In Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

of n dimensions, the unit sphere is the set of all points

which satisfy the equation

and the closed unit ball is the set of all points satisfying the inequality

General area and volume formulas

The classical equation of a unit sphere is that of the ellipsoid with a radius of 1 and no alterations to the x-, y-, or z- axes:

The volume of the unit ball in n-dimensional Euclidean space, and the surface area of the unit sphere, appear in many important formulas of analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

. The volume of the unit ball in n dimensions, which we denote V_n, can be expressed by making use of the Gamma function

Gamma function

In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

. It is

where n!! is the double factorial.

The hypervolume of the (n–1)-dimensional unit sphere (i.e., the "area" of the surface of the n-dimensional unit ball), which we denote A_n, can be expressed as

where the last equality holds only for n > 0.

The surface areas and the volumes for some values of

are as follows:


0	0.000	1.000
1	2.000	2.000
2	6.283	3.142
3	12.57	4.189
4	19.74	4.935
5	26.32	5.264
6	31.01	5.168
7	33.07	4.725
8	32.47	4.059
9	29.69	3.299
10	25.50	2.550

where the decimal expanded values for n ≥ 2 are rounded to the displayed precision.

Recursion

The A_n values satisfy the recursion:

for

.

The V_n values satisfy the recursion:

for

Fractional dimensions

The formulae for A_n and V_n can be computed for any real number n ≥ 0, and there are circumstances under which it is appropriate to seek the sphere area or ball volume when n is not a non-negative integer.

Other radii

The surface area of an (n–1)-dimensional sphere with radius r is A_n rⁿ⁻¹ and the volume of an n-dimensional ball with radius r is V_n rⁿ. For instance, the area is for the surface of the three-dimensional ball of radius r. The volume is for the three-dimensional ball of radius r.

Unit balls in normed vector spaces

More precisely, the open unit ball in a normed vector space

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

, with the norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

, is

It is the interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

of the closed unit ball of (V,||·||),

The latter is the disjoint union of the former and their common border, the unit sphere of (V,||·||),

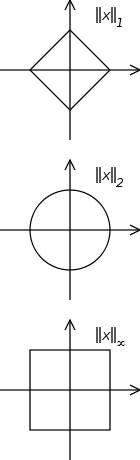
The 'shape' of the unit ball is entirely dependent on the chosen norm; it may well have 'corners', and for example may look like [−1,1]ⁿ, in the case of the norm l_∞ in Rⁿ. The round ball is understood as the usual Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

norm, based in the finite dimensional case on the Euclidean distance

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

; its boundary is what is usually meant by the unit sphere. Here are some images of the unit ball for the two-dimensional

space

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

for various values of p (the unit ball being concave for p < 1 and convex for p ≥ 1):

These illustrate why the condition p ≥ 1 is necessary in the definition of the

norm, as the unit ball in any normed space must be convex

Convex

'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...

as a consequence of the triangle inequality

Triangle inequality

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

.

Note that for the circumferences

of the two-dimensional unit balls we have:

is the maximum value.

is the minimum value.

Metric spaces

All three of the above definitions can be straightforwardly generalized to a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

, with respect to a chosen origin. However, topological considerations (interior, closure, border) need not apply in the same way (e.g., in ultrametric spaces, all of the three are simultaneously open and closed sets), and the unit sphere may even be empty in some metric spaces.

Quadratic forms

If V is a linear space with a real quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

F:V → R, then { p ∈ V : F(p) = 1 } is sometimes called the unit quasi-sphere of V. For example, the quadratic form

corresponds to a unit quasi-sphere that is a hyperbola which plays the role of the "unit circle" in the plane of split-complex number

Split-complex number

In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...

s. Similarly, quadratic form x² yields a pair of lines for the unit quasi-sphere in the dual number

Dual number

In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...

plane.