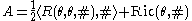Weitzenbock identity
Encyclopedia
In mathematics
, in particular in differential geometry, mathematical physics
, and representation theory
a Weitzenböck identity (named after Roland Weitzenböck) expresses a relationship between two second-order elliptic operator
s on a manifold with the same leading symbol. Usually Weitzenböck formulae are implemented for G-invariant self-adjoint operators between vector bundles associated to some principal G-bundle
, although the precise conditions under which such a formula exists are difficult to formulate. Instead of attempting to be completely general, then, this article presents three examples of Weitzenböck identities: from Riemannian geometry, spin geometry, and complex analysis.
there are two notions of the Laplacian on differential forms over an oriented compact Riemannian manifold M. The first definition uses the divergence operator
δ defined as the formal adjoint of the de Rham operator d:
where α is any p-form and β is any (p+1)-form, and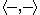
is the metric induced on the bundle of (p+1)-forms. The usual form Laplacian is then given by
On the other hand, the Levi-Civita connection
supplies a differential operator
where ΩpM is the bundle of p-forms and T*M is the cotangent bundle
of M. The Bochner Laplacian is given by
where
is the adjoint of 
.
The Weitzenböck formula then asserts that
where A is a linear operator of order zero involving only the curvature.
The precise form of A is given, up to an overall sign depending on curvature conventions, by
where
ð, then one may form the spin Laplacian Δ = ð2 on the spin bundle. On the other hand, the Levi-Civita connection extends to the spin bundle to yield a differential operator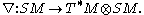
As in the case of Riemannian manifolds, let
. This is another self-adjoint operator and, moreover, has the same leading symbol as the spin Laplacian. The Weitzenböck formula yields: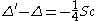
where Sc is the scalar curvature. This result is also known as the Lichnerowicz formula
.
, there is a Weitzenböck formula relating the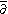
-Laplacian (see Dolbeault complex) and the Euclidean Laplacian on (p,q)-forms
. Specifically, let
According to the Weitzenböck formula, if α ε Ω(p,q)M, then
where A is an operator of order zero involving the curvature. Specifically, if
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in differential geometry, mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
a Weitzenböck identity (named after Roland Weitzenböck) expresses a relationship between two second-order elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s on a manifold with the same leading symbol. Usually Weitzenböck formulae are implemented for G-invariant self-adjoint operators between vector bundles associated to some principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
, although the precise conditions under which such a formula exists are difficult to formulate. Instead of attempting to be completely general, then, this article presents three examples of Weitzenböck identities: from Riemannian geometry, spin geometry, and complex analysis.
Riemannian geometry
In Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
there are two notions of the Laplacian on differential forms over an oriented compact Riemannian manifold M. The first definition uses the divergence operator
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
δ defined as the formal adjoint of the de Rham operator d:
where α is any p-form and β is any (p+1)-form, and
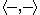is the metric induced on the bundle of (p+1)-forms. The usual form Laplacian is then given by
-
- Δ = dδ + δd.
On the other hand, the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
supplies a differential operator
where ΩpM is the bundle of p-forms and T*M is the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of M. The Bochner Laplacian is given by
where
is the adjoint of .The Weitzenböck formula then asserts that
where A is a linear operator of order zero involving only the curvature.
The precise form of A is given, up to an overall sign depending on curvature conventions, by
where
- R is the Riemann curvature tensor,
- Ric is the Ricci tensor,
is the alternation map,
is the universal derivation inverse to θ on 1-forms.
Spin geometry
If M is an oriented spin manifold with Dirac operatorDirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
ð, then one may form the spin Laplacian Δ = ð2 on the spin bundle. On the other hand, the Levi-Civita connection extends to the spin bundle to yield a differential operator
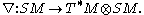
As in the case of Riemannian manifolds, let
. This is another self-adjoint operator and, moreover, has the same leading symbol as the spin Laplacian. The Weitzenböck formula yields: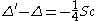where Sc is the scalar curvature. This result is also known as the Lichnerowicz formula
Lichnerowicz formula
The Lichnerowicz formula is a fundamental equation in the analysis of spinors on pseudo-Riemannian manifolds. In dimension 4, it forms a piece of Seiberg–Witten theory and other aspects of gauge theory. It is named after noted mathematician André Lichnerowicz who proved it in 1963...
.
Complex differential geometry
If M is a compact Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, there is a Weitzenböck formula relating the
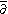-Laplacian (see Dolbeault complex) and the Euclidean Laplacian on (p,q)-formsComplex differential form
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
. Specifically, let
-
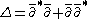, and -
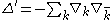in a unitary frame at each point.
According to the Weitzenböck formula, if α ε Ω(p,q)M, then
- Δ'α − Δα = A(α)
where A is an operator of order zero involving the curvature. Specifically, if
-
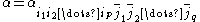in a unitary frame, then
with k in the s-th place.
Other Weitzenböck identities
- In conformal geometryConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
there is a Weitzenböck formula relating a particular pair of differential operators defined on the tractor bundleTractor bundleIn conformal geometry, the tractor bundle is a particular vector bundle constructed on a conformal manifold whose fibres form an effective representation of the conformal group ....
. See Branson, T. and Gover, A.R., "Conformist Invariant Operators, Differential Forms, Cohomology and a Generalisation of Q-Curvature", Communications in Partial Differential Equations, 30 (2005) 1611-1669.