
Latin square
Encyclopedia

Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
and in experimental design
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. Here is an example:
| A | B | C |
| C | A | B |
| B | C | A |
The name "Latin square" is motivated by mathematical papers by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who used Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
characters as symbols.
Of course, other symbols can be used instead of Latin letters: in the above example, the alphabetic sequence A, B, C can be replaced by the integer sequence 1, 2, 3.
Overview of uses
Latin squares are used in statistics and in mathematics.- In the design of experimentsDesign of experimentsIn general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, Latin squares are a special case of row-column designs for two blocking factorsBlocking (statistics)In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. For example, an experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male...
: Many row-column designs are constructed by concatenating Latin squares. - In algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, Latin squares are generalizations of groupsGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
; in fact, Latin squares are characterized as being the multiplication tableMultiplication tableIn mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
s (Cayley tableCayley tableA Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
s) of quasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
s. Other applications include error correcting codes.
Reduced form
A Latin square is said to be reduced (also, normalized or in standard form) if both its first row and its first column are in their natural order. For example, the above Latin square is not reduced because its first column is A, C, B rather than A, B, C.We can make any Latin square reduced by permuting (reordering) the rows and columns. Here switching the above matrix's second and third rows yields
| A | B | C |
| B | C | A |
| C | A | B |
which is reduced: Both its first row and its first column are alphabetically ordered A, B, C.
Orthogonal array representation
If each entry of an n × n Latin square is written as a triple (r,c,s), where r is the row, c is the column, and s is the symbol, we obtain a set of n2 triples called the orthogonal array representation of the square. For example, the orthogonal array representation of the first Latin square displayed above is:- { (1,1,1),(1,2,2),(1,3,3),(2,1,2),(2,2,3),(2,3,1),(3,1,3),(3,2,1),(3,3,2) },
where for example the triple (2,3,1) means that in row 2 and column 3 there is the symbol 1. The definition of a Latin square can be written in terms of orthogonal arrays:
- A Latin square is the set of all triples (r,c,s), where 1 ≤ r, c, s ≤ n, such that all ordered pairs (r,c) are distinct, all ordered pairs (r,s) are distinct, and all ordered pairs (c,s) are distinct.
For any Latin square, there are n2 triples since choosing any two uniquely determines the third. (Otherwise, an ordered pair would appear more than once in the Latin square.)
The orthogonal array representation shows that rows, columns and symbols play rather similar roles, as will be made clear below.
Equivalence classes of Latin squares
Many operations on a Latin square produce another Latin square (for example, turning it upside down).If we permute the rows, permute the columns, and permute the names of the symbols of a Latin square, we obtain a new Latin square said to be isotopic to the first. Isotopism is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, so the set of all Latin squares is divided into subsets, called isotopy classes, such that two squares in the same class are isotopic and two squares in different classes are not isotopic.
Another type of operation is easiest to explain using the orthogonal array representation of the Latin square. If we systematically and consistently reorder the three items in each triple, another orthogonal array (and, thus, another Latin square) is obtained. For example, we can replace each triple (r,c,s) by (c,r,s) which corresponds to transposing the square (reflecting about its main diagonal), or we could replace each triple (r,c,s) by (c,s,r), which is a more complicated operation. Altogether there are 6 possibilities including "do nothing", giving us 6 Latin squares called the conjugates (also parastrophes) of the original square.
Finally, we can combine these two equivalence operations: two Latin squares are said to be paratopic, also main class isotopic, if one of them is isotopic to a conjugate of the other. This is again an equivalence relation, with the equivalence classes called main classes, species, or paratopy classes. Each main class contains up to 6 isotopy classes.
Number
There is no known easily-computable formula for the number L(n) of n × n Latin squares with symbols 1,2,...,n. The most accurate upper and lower bounds known for large n are far apart. One classic result is
(this given by van Lint and Wilson).
Here we will give all the known exact values. It can be seen that the numbers grow exceedingly quickly. For each n, the number of Latin squares altogether is n! (n-1)! times the number of reduced Latin squares .
| n | reduced Latin squares of size n | all Latin squares of size n |
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 1 | 12 |
| 4 | 4 | 576 |
| 5 | 56 | 161280 |
| 6 | 9408 | 812851200 |
| 7 | 16942080 | 61479419904000 |
| 8 | 535281401856 | 108776032459082956800 |
| 9 | 377597570964258816 | 5524751496156892842531225600 |
| 10 | 7580721483160132811489280 | 9982437658213039871725064756920320000 |
| 11 | 5363937773277371298119673540771840 | 776966836171770144107444346734230682311065600000 |
For each n, each isotopy class contains up to (n!)3 Latin squares (the exact number varies), while each main class contains either 1, 2, 3 or 6 isotopy classes.
| n | main classes | isotopy classes |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 2 | 2 |
| 5 | 2 | 2 |
| 6 | 12 | 22 |
| 7 | 147 | 564 |
| 8 | 283657 | 1676267 |
| 9 | 19270853541 | 115618721533 |
| 10 | 34817397894749939 | 208904371354363006 |
| 11 | 2036029552582883134196099 | 12216177315369229261482540 |
Examples
We give one example of a Latin square from each main class up to order 5.

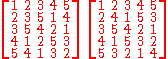
They present, respectively, the multiplication tables of the following groups:
- {0} – the trivial 1-element group
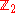 – the binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
– the binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
group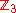 – cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
– cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 3 – the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
– the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...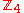 – cyclic group of order 4
– cyclic group of order 4 – cyclic group of order 5
– cyclic group of order 5- the last one is an example of a quasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, or rather a loop, which is not associative.
Error correcting codes
Sets of Latin squares that are orthogonal to each other have found an application as error correcting codes in situations where communication is disturbed by more types of noise than simple white noiseWhite noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
, such as when attempting to transmit broadband Internet over powerlines.
Firstly, the message is sent by using several frequencies, or channels, a common method that makes the signal less vulnerable to noise at any one specific frequency. A letter in the message to be sent is encoded by sending a series of signals at different frequencies at successive time intervals. In the example below, the letters A to L are encoded by sending signals at four different frequencies, in four time slots. The letter C, for instance, is encoded by first sending at frequency 3, then 4, 1 and 2.

The encoding of the twelve letters are formed from three Latin squares that are orthogonal to each other. Now imagine that there's added noise in channels 1 and 2 during the whole transmission. The letter A would then be picked up as:

In other words, in the first slot we receive signals from both frequency 1 and frequency 2; while the third slot has signals from frequencies 1, 2 and 3. Because of the noise, we can no longer tell if the first two slots were 1,1 or 1,2 or 2,1 or 2,2. But the 1,2 case is the only one that yields a sequence matching a letter in the above table, the letter A.
Similarly, we may imagine a burst of static over all frequencies in the third slot:
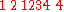
Again, we are able to infer from the table of encodings that it must have been the letter A being transmitted. The number of errors this code can spot is one less than the number of time slots. It has also been proved that if the number of frequencies is a prime or a power of a prime, the orthogonal Latin squares produce error detecting codes that are as efficient as possible.
Mathematical puzzles
The problem of determining if a partially filled square can be completed to form a Latin square is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
The popular Sudoku
Mathematics of Sudoku
The class of Sudoku puzzles consists of a partially completed row-column grid of cells partitioned into N regions each of size N cells, to be filled in using a prescribed set of N distinct symbols , so that each row, column and region contains exactly one of each element of the set...
puzzles are a special case of Latin squares; any solution to a Sudoku puzzle is a Latin square. Sudoku imposes the additional restriction that nine particular 3×3 adjacent subsquares must also contain the digits 1–9 (in the standard version). The more recent KenKen
KenKen
KenKen or KenDoku is a style of arithmetic and logic puzzle invented in 2004 by the Japanese math teacher Tetsuya Miyamoto, an innovator who says he practices "the art of teaching without teaching". He intends the puzzles as an instruction-free method of training the brain...
puzzles are also examples of Latin squares.
Heraldry
The Latin square also figures in the blazon of the arms of the Statistical Society of Canada. Also, it appears in the logo of the International Biometric SocietyInternational Biometric Society
The International Biometric Society is an international professional and academic society promoting the development and application of statistical and mathematical theory and methods in the biosciences....
.
See also
- Latin hypercube samplingLatin hypercube samplingLatin hypercube sampling is a statistical method for generating a distribution of plausible collections of parameter values from a multidimensional distribution. The sampling method is often applied in uncertainty analysis....
- Graeco-Latin squareGraeco-Latin squareIn mathematics, a Graeco-Latin square or Euler square or orthogonal Latin squares of order n over two sets S and T, each consisting of n symbols, is an n×n arrangement of cells, each cell containing an ordered pair , where s is in S and t is in T, such that every row and every column contains...
- Magic SquareMagic squareIn recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
- Problems in Latin squaresProblems in Latin squaresIn mathematics, the theory of Latin squares is an active research area with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings...
- Small Latin squares and quasigroupsSmall Latin squares and quasigroupsBelow the Latin squares and quasigroups of some small orders are considered.-Order 1:...
- Mathematics of SudokuMathematics of SudokuThe class of Sudoku puzzles consists of a partially completed row-column grid of cells partitioned into N regions each of size N cells, to be filled in using a prescribed set of N distinct symbols , so that each row, column and region contains exactly one of each element of the set...
- FutoshikiFutoshikior Unequal is a logic puzzle game from Japan. Its name means "inequality". It is also spelled hutosiki .The puzzle is played on a square grid, such as 5 x 5. The objective is to place the numbers 1 to 5 such that each row, and column contains each of the digits 1 to 5. Some digits may be given...
- Rook's graphRook's graphIn graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
, a graph that has Latin squares as its coloringsGraph coloringIn graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
. - Eight queens puzzleEight queens puzzleThe eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens attack each other. Thus, a solution requires that no two queens share the same row, column, or diagonal...
- Block design
- Word squareWord squareA word square is a special type of acrostic. It consists of a set of words written out in a square grid, such that the same words can be read both horizontally and vertically. The number of words, which is equal to the number of letters in each word, is known as the "order" of the square...
External links
- Latin Squares in the Encyclopaedia of MathematicsEncyclopaedia of MathematicsThe Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....
- Latin Squares in Java at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Infinite Latin Square (Java) at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Magic Square in Latin Square

