
Frame fields in general relativity
Encyclopedia
In general relativity
, a frame field (also called a tetrad or vierbein) is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime
. The timelike unit vector field is often denoted by and the three spacelike unit vector fields by
and the three spacelike unit vector fields by 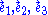 . All tensor
. All tensor
ial quantities defined on the manifold
can be expressed using the frame field and its dual
coframe field.
Frames were introduced into general relativity by Hermann Weyl
in 1929.
The general theory of tetrads (and analogs in dimensions other than 4) is described in the article on Cartan formalism; the index notation for tetrads is explained in tetrad (index notation).
s of the timelike unit vector field are the worldlines of these observers, and at each event along a given worldline, the three spacelike unit vector fields specify the spatial triad carried by the observer. The triad may be thought of as defining the spatial coordinate axes of a local laboratory frame, which is valid very near the observer's worldline.
In general, the worldlines of these observers need not be timelike geodesic
s. If any of the worldlines bends away from a geodesic path in some region, we can think of the observers as test particles that accelerate
by using ideal rocket engines with a thrust equal to the magnitude of their acceleration vector
. Alternatively, if our observer is attached to a bit of matter in a ball of fluid
in hydrostatic equilibrium
, this bit of matter will in general be accelerated outward by the net effect of pressure
holding up the fluid ball against the attraction of its own gravity. Other possibilities include an observer attached to a free charged test particle in an electrovacuum solution
, which will of course be accelerated by the Lorentz force
, or an observer attached to a spinning test particle, which may be accelerated by a spin-spin force.
It is important to recognize that frames are geometric objects. That is, vector fields make sense (in a smooth manifold) independently of choice of a coordinate chart, and (in a Lorentzian manifold), so do the notions of orthogonality and length. Thus, just like vector fields and other geometric quantities, frame fields can be represented in various coordinate charts. But computations of the components of tensorial quantities, with respect to a given frame, will always yield the same result, whichever coordinate chart is used to represent the frame.
These fields are required to write the Dirac equation in curved spacetime.
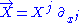
(Here, the Einstein summation convention is used, and the vector fields are thought of as first order linear
differential operator
s, and the components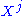 are often called contravariant components
are often called contravariant components
.) In particular, the vector fields in the frame can be expressed this way: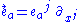
In "designing" a frame, one naturally needs to ensure, using the given metric
, that the four vector fields are everywhere orthonormal.
Once a signature is adopted (in the case of a four-dimensional Lorentzian manifold, the signature is -1 + 3), by duality every vector has a dual covector and conversely. Thus, every frame field is associated with a unique coframe field, and vice versa.
can be specified by writing down a coframe in terms of a coordinate basis and stipulating that the metric tensor is given by
This is just a fancy way of saying that the coframe is orthonormal. Whether this is used to obtain the metric tensor after writing down the frame (and passing to the dual coframe), or starting with the metric tensor and using it to verify that a frame has been obtained by other means, it must always hold true.
 , has two indices:
, has two indices: 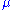 labels the general spacetime coordinate and
labels the general spacetime coordinate and  labels the local lorentz spacetime or local laboratory coordinates.
labels the local lorentz spacetime or local laboratory coordinates.
The vierbein field or frame fields can be regarded as the square root of the metric tensor
,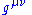 , since in a coordinate basis,
, since in a coordinate basis,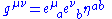
where is the Lorentz metric.
is the Lorentz metric.
Local lorentz indices are raised and lowered with the lorentz metric in the same way as general spacetime coordinates are raised and lowered with the metric tensor. For example:

The vierbein fields enables conversion between spacetime and local lorentz indices. For example: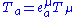
The vierbein field itself can be manipulated in the same fashion: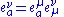 , since
, since 
And these can combine.
A few more examples: Spacetime and local lorentz coordinates can be mixed together: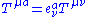
The local lorentz coordinates transform differently from the general spacetime coordinates. Under a general coordinate transformation we have:

whilst under a local lorentz transformation we have:
 .
.
pairwise vanish. Except in locally flat regions, at least some Lie brackets of vector fields from a frame will not vanish. The resulting baggage needed to compute with them is acceptable, as components of tensorial objects with respect to a frame (but not with respect to a coordinate basis) have a direct interpretation in terms of measurements made by the family of ideal observers corresponding the frame.
Coordinate basis vectors can very well be null, which, by definition, cannot happen for frame vectors.
or electrovacuum solution
s, the physical experience of inertial observers (who feel no forces) may be of particular interest. The mathematical characterization of an inertial frame is very simple: the integral curve
s of the timelike unit vector field
must define a geodesic
congruence
, or in other words, its acceleration vector must vanish: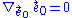
It is also often desirable to ensure that the spatial triad carried by each observer does not rotate. In this case, the triad can be viewed as being gyrostabilized
. The criterion for a nonspinning inertial (NSI) frame is again very simple: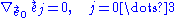
This says that as we move along the worldline of each observer, their spatial triad is parallel-transported. Nonspinning inertial frames hold a special place in general relativity, because they are as close as we can get in a curved Lorentzian manifold to the Lorentz frames used in special relativity
(these are special nonspinning inertial frames in the Minkowski vacuum).
More generally, if the acceleration of our observers is nonzero, , we can replace the covariant derivatives
, we can replace the covariant derivatives
with the (spatially projected) Fermi-Walker derivatives to define a nonspinning frame.
Given a Lorentzian manifold, we can find infinitely many frame fields, even if we require additional properties such as inertial motion. However, a given frame field might very well be defined on only part of the manifold.
that models spacetime outside an isolated nonspinning spherically symmetric massive object, such as a star. In most textbooks one finds the metric tensor written in terms of a static polar spherical chart, as follows:

More formally, the metric tensor can be expanded with respect to the coordinate cobasis as
A coframe can be read off from this expression: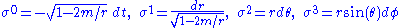
To see that this coframe really does correspond to the Schwarzschild metric tensor, just plug this coframe into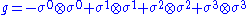
The frame dual to the coframe is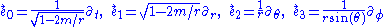
(The minus sign on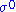 ensures that
ensures that 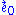 is future pointing.) This is the frame that models the experience of static observers who use rocket engines to "hover" over the massive object. The thrust they require to maintain their position is given by the magnitude of the acceleration vector
is future pointing.) This is the frame that models the experience of static observers who use rocket engines to "hover" over the massive object. The thrust they require to maintain their position is given by the magnitude of the acceleration vector
This is radially outward pointing, since the observers need to accelerate away from the object to avoid falling toward it. On the other hand, the spatially projected Fermi derivatives of the spatial basis vectors (with respect to ) vanish, so this is a nonspinning frame.
) vanish, so this is a nonspinning frame.
The components of various tensorial quantities with respect to our frame and its dual coframe can now be computed.
For example, the tidal tensor
for our static observers is defined using tensor notation (for a coordinate basis) as
where we write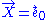 to avoid cluttering the notation. Its only non-zero components with respect to our coframe turn out to be
to avoid cluttering the notation. Its only non-zero components with respect to our coframe turn out to be
The corresponding coordinate basis components are
(A quick note concerning notation: many authors put caret
s over abstract indices referring to a frame. When writing down specific components, it is convenient to denote frame components by 0,1,2,3 and coordinate components by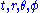 . Since an expression like
. Since an expression like  doesn't make sense as a tensor equation, there should be no possibility of confusion.)
doesn't make sense as a tensor equation, there should be no possibility of confusion.)
Compare the tidal tensor
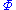 of Newtonian gravity, which is the traceless part of the Hessian
of Newtonian gravity, which is the traceless part of the Hessian
of the gravitational potential . Using tensor notation for a tensor field defined on three-dimensional euclidean space, this can be written
. Using tensor notation for a tensor field defined on three-dimensional euclidean space, this can be written
The reader may wish to crank this through (notice that the trace term actually vanishes identically when U is harmonic) and compare results with the following elementary approach:
we can compare the gravitational forces on two nearby observers lying on the same radial line: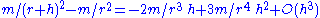
Because in discussing tensors we are dealing with multilinear algebra
, we retain only first order terms, so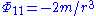 . Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere
. Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere  . Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
. Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
By using the small angle approximation, we have ignored all terms of order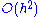 , so the tangential components are
, so the tangential components are 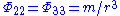 . Here, we are referring to the obvious frame obtained from the polar spherical chart for our three-dimensional euclidean space:
. Here, we are referring to the obvious frame obtained from the polar spherical chart for our three-dimensional euclidean space: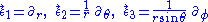
Plainly, the coordinate components computed above don't even scale the right way, so they clearly cannot correspond to what an observer will measure even approximately. (By coincidence, the Newtonian tidal tensor components agree exactly with the relativistic tidal tensor components we wrote out above.)
computed above don't even scale the right way, so they clearly cannot correspond to what an observer will measure even approximately. (By coincidence, the Newtonian tidal tensor components agree exactly with the relativistic tidal tensor components we wrote out above.)
 direction by an undetermined boost parameter (depending on the radial coordinate), compute the acceleration vector of the new undetermined frame, set this equal to zero, and solve for the unknown boost parameter. The result will be a frame which we can use to study the physical experience of observers who fall freely and radially toward the massive object. By appropriately choosing an integration constant, we obtain the frame of Lemaître observers, who fall in from rest at spatial infinity. (This phrase doesn't make sense, but the reader will no doubt have no difficulty in understanding our meaning.) In the static polar spherical chart, this frame can be written
direction by an undetermined boost parameter (depending on the radial coordinate), compute the acceleration vector of the new undetermined frame, set this equal to zero, and solve for the unknown boost parameter. The result will be a frame which we can use to study the physical experience of observers who fall freely and radially toward the massive object. By appropriately choosing an integration constant, we obtain the frame of Lemaître observers, who fall in from rest at spatial infinity. (This phrase doesn't make sense, but the reader will no doubt have no difficulty in understanding our meaning.) In the static polar spherical chart, this frame can be written
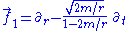
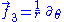

Note that
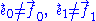 , and that
, and that 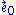 "leans inwards", as it should, since its integral curves are timelike geodesics representing the world lines of infalling observers. Indeed, since the covariant derivatives of all four basis vectors (taken with respect to
"leans inwards", as it should, since its integral curves are timelike geodesics representing the world lines of infalling observers. Indeed, since the covariant derivatives of all four basis vectors (taken with respect to  ) vanish identically, our new frame is a nonspinning inertial frame.
) vanish identically, our new frame is a nonspinning inertial frame.
If our massive object is in fact a (nonrotating) black hole
, we probably wish to follow the experience of the Lemaître observers as they fall through the event horizon
at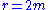 . Since the static polar spherical coordinates have a coordinate singularity at the horizon, we'll need to switch to a more appropriate coordinate chart. The simplest possible choice is to define a new time coordinate by
. Since the static polar spherical coordinates have a coordinate singularity at the horizon, we'll need to switch to a more appropriate coordinate chart. The simplest possible choice is to define a new time coordinate by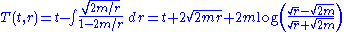
This gives the Painlevé chart
. The new line element is

With respect to the Painlevé chart, the Lemaître frame is



Notice that their spatial triad looks exactly like the frame for three-dimensional euclidean space which we mentioned above (when we computed the Newtonian tidal tensor). Indeed, the spatial hyperslices turn out to be locally isometric to flat three-dimensional euclidean space! (This is a remarkable and rather special property of the Schwarzschild vacuum; most spacetimes do not admit a slicing into flat spatial sections.)
turn out to be locally isometric to flat three-dimensional euclidean space! (This is a remarkable and rather special property of the Schwarzschild vacuum; most spacetimes do not admit a slicing into flat spatial sections.)
The tidal tensor taken with respect to the Lemaître observers is
where we write to avoid cluttering the notation. This is a different tensor from the one we obtained above, because it is defined using a different family of observers. Nonetheless, its nonvanishing components look familiar:
to avoid cluttering the notation. This is a different tensor from the one we obtained above, because it is defined using a different family of observers. Nonetheless, its nonvanishing components look familiar:  . (This is again a rather special property of the Schwarzschild vacuum.)
. (This is again a rather special property of the Schwarzschild vacuum.)
Notice that there is simply no way of defining static observers on or inside the event horizon. On the other hand, the Lemaître observers are not defined on the entire exterior region covered by the static polar spherical chart either, so in these examples, neither the Lemaître frame nor the static frame are defined on the entire manifold.
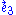 direction by an undetermined parameter (depending on the radial coordinate), compute the acceleration vector, and require that this vanish in the equatorial plane
direction by an undetermined parameter (depending on the radial coordinate), compute the acceleration vector, and require that this vanish in the equatorial plane 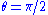 . The new Hagihara frame describes the physical experience of observers in stable circular orbits around our massive object. It was apparently first discussed by the distinguished (and mathematically gifted) astronomer Yusuke Hagihara
. The new Hagihara frame describes the physical experience of observers in stable circular orbits around our massive object. It was apparently first discussed by the distinguished (and mathematically gifted) astronomer Yusuke Hagihara
.
In the static polar spherical chart, the Hagihara frame is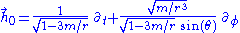
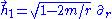
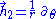
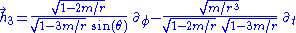
which in the equatorial plane becomes
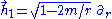

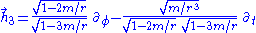
The tidal tensor where
where  turns out to be given (in the equatorial plane) by
turns out to be given (in the equatorial plane) by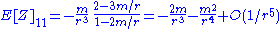
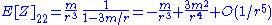

Thus, compared to a static observer hovering at a given coordinate radius,
a Hagihara observer in a stable circular orbit with the same coordinate radius will measure radial tidal forces which are slightly larger in magnitude, and transverse tidal forces which are no longer isotropic (but slightly larger orthogonal to the direction of motion).
Note that the Hagihara frame is only defined on the region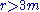 . Indeed, stable circular orbits only exist on
. Indeed, stable circular orbits only exist on 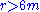 , so the frame should not be used inside this locus.
, so the frame should not be used inside this locus.
Computing Fermi derivatives shows that the frame field just given is in fact spinning with respect to a gyrostabilized frame. The principal reason why is easy to spot: in this frame, each Hagihara observer keeps his spatial vectors radially aligned, so rotate about
rotate about 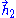 as the observer orbits around the central massive object. However, after correcting for this observation, a small precession of the spin axis of a gyroscope carried by a Hagihara observer still remains; this is the de Sitter precession effect (also called the geodetic precession effect).
as the observer orbits around the central massive object. However, after correcting for this observation, a small precession of the spin axis of a gyroscope carried by a Hagihara observer still remains; this is the de Sitter precession effect (also called the geodetic precession effect).
or pseudo-Riemannian manifold
, a frame field is a set of orthonormal vector fields which forms a basis
for the tangent space
at each point in the manifold. As before, frames can be specified in terms of a given coordinate basis, and in a non-flat region, some of their pairwise Lie brackets will fail to vanish.
In fact, given any inner-product space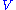 , we can define a new space consisting of all tuples of orthonormal bases for
, we can define a new space consisting of all tuples of orthonormal bases for 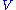 . Applying this construction to each tangent space yields the orthonormal frame bundle
. Applying this construction to each tangent space yields the orthonormal frame bundle
of a (pseudo-)Riemannian manifold and a frame field is a section of this bundle. More generally still, we can consider frame bundles associated to any vector bundle
, or even arbitrary principal
fiber bundle
s. The notation becomes a bit more involved because it is harder to avoid distinguishing between indices referring to the base, and indices referring to the fiber. Many authors speak of internal components when referring to components indexed by the fiber.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a frame field (also called a tetrad or vierbein) is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. The timelike unit vector field is often denoted by
 and the three spacelike unit vector fields by
and the three spacelike unit vector fields by 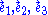 . All tensor
. All tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
ial quantities defined on the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
can be expressed using the frame field and its dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
coframe field.
Frames were introduced into general relativity by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in 1929.
The general theory of tetrads (and analogs in dimensions other than 4) is described in the article on Cartan formalism; the index notation for tetrads is explained in tetrad (index notation).
Physical interpretation
Frame fields always correspond to a family of ideal observers immersed in the given spacetime; the integral curveIntegral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the timelike unit vector field are the worldlines of these observers, and at each event along a given worldline, the three spacelike unit vector fields specify the spatial triad carried by the observer. The triad may be thought of as defining the spatial coordinate axes of a local laboratory frame, which is valid very near the observer's worldline.
In general, the worldlines of these observers need not be timelike geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. If any of the worldlines bends away from a geodesic path in some region, we can think of the observers as test particles that accelerate
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
by using ideal rocket engines with a thrust equal to the magnitude of their acceleration vector
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
. Alternatively, if our observer is attached to a bit of matter in a ball of fluid
Fluid solution
In general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
in hydrostatic equilibrium
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
, this bit of matter will in general be accelerated outward by the net effect of pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
holding up the fluid ball against the attraction of its own gravity. Other possibilities include an observer attached to a free charged test particle in an electrovacuum solution
Electrovacuum solution
In general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
, which will of course be accelerated by the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, or an observer attached to a spinning test particle, which may be accelerated by a spin-spin force.
It is important to recognize that frames are geometric objects. That is, vector fields make sense (in a smooth manifold) independently of choice of a coordinate chart, and (in a Lorentzian manifold), so do the notions of orthogonality and length. Thus, just like vector fields and other geometric quantities, frame fields can be represented in various coordinate charts. But computations of the components of tensorial quantities, with respect to a given frame, will always yield the same result, whichever coordinate chart is used to represent the frame.
These fields are required to write the Dirac equation in curved spacetime.
Specifying a frame
To write down a frame, a coordinate chart on the Lorentzian manifold needs to be chosen. Then, every vector field on the manifold can be written down as a linear combination of the four coordinate basis vector fields: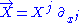
(Here, the Einstein summation convention is used, and the vector fields are thought of as first order linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s, and the components
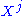 are often called contravariant components
are often called contravariant componentsCovariance and contravariance
In multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis from one coordinate system to another. When one coordinate system is just a rotation of the other, this...
.) In particular, the vector fields in the frame can be expressed this way:
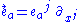
In "designing" a frame, one naturally needs to ensure, using the given metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, that the four vector fields are everywhere orthonormal.
Once a signature is adopted (in the case of a four-dimensional Lorentzian manifold, the signature is -1 + 3), by duality every vector has a dual covector and conversely. Thus, every frame field is associated with a unique coframe field, and vice versa.
Specifying the metric using a coframe
Alternatively, the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
can be specified by writing down a coframe in terms of a coordinate basis and stipulating that the metric tensor is given by

This is just a fancy way of saying that the coframe is orthonormal. Whether this is used to obtain the metric tensor after writing down the frame (and passing to the dual coframe), or starting with the metric tensor and using it to verify that a frame has been obtained by other means, it must always hold true.
Relationship with metric tensor, in a coordinate basis
The vierbein field, , has two indices:
, has two indices: 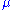 labels the general spacetime coordinate and
labels the general spacetime coordinate and  labels the local lorentz spacetime or local laboratory coordinates.
labels the local lorentz spacetime or local laboratory coordinates.The vierbein field or frame fields can be regarded as the square root of the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
,
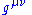 , since in a coordinate basis,
, since in a coordinate basis,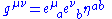
where
 is the Lorentz metric.
is the Lorentz metric.Local lorentz indices are raised and lowered with the lorentz metric in the same way as general spacetime coordinates are raised and lowered with the metric tensor. For example:

The vierbein fields enables conversion between spacetime and local lorentz indices. For example:
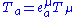
The vierbein field itself can be manipulated in the same fashion:
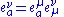 , since
, since 
And these can combine.

A few more examples: Spacetime and local lorentz coordinates can be mixed together:
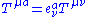
The local lorentz coordinates transform differently from the general spacetime coordinates. Under a general coordinate transformation we have:

whilst under a local lorentz transformation we have:
 .
.Comparison with coordinate basis
Coordinate basis vectors have the special property that their Lie bracketsLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
pairwise vanish. Except in locally flat regions, at least some Lie brackets of vector fields from a frame will not vanish. The resulting baggage needed to compute with them is acceptable, as components of tensorial objects with respect to a frame (but not with respect to a coordinate basis) have a direct interpretation in terms of measurements made by the family of ideal observers corresponding the frame.
Coordinate basis vectors can very well be null, which, by definition, cannot happen for frame vectors.
Nonspinning and inertial frames
Some frames are nicer than others. Particularly in vacuumVacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
or electrovacuum solution
Electrovacuum solution
In general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
s, the physical experience of inertial observers (who feel no forces) may be of particular interest. The mathematical characterization of an inertial frame is very simple: the integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the timelike unit vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
must define a geodesic
Geodesic (general relativity)
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic...
congruence
Congruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
, or in other words, its acceleration vector must vanish:
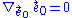
It is also often desirable to ensure that the spatial triad carried by each observer does not rotate. In this case, the triad can be viewed as being gyrostabilized
Gyroscope
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
. The criterion for a nonspinning inertial (NSI) frame is again very simple:
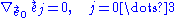
This says that as we move along the worldline of each observer, their spatial triad is parallel-transported. Nonspinning inertial frames hold a special place in general relativity, because they are as close as we can get in a curved Lorentzian manifold to the Lorentz frames used in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
(these are special nonspinning inertial frames in the Minkowski vacuum).
More generally, if the acceleration of our observers is nonzero,
 , we can replace the covariant derivatives
, we can replace the covariant derivatives
with the (spatially projected) Fermi-Walker derivatives to define a nonspinning frame.
Given a Lorentzian manifold, we can find infinitely many frame fields, even if we require additional properties such as inertial motion. However, a given frame field might very well be defined on only part of the manifold.
Example: Static observers in Schwarzschild vacuum
It will be instructive to consider in some detail a few simple examples. Consider the famous Schwarzschild vacuumSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
that models spacetime outside an isolated nonspinning spherically symmetric massive object, such as a star. In most textbooks one finds the metric tensor written in terms of a static polar spherical chart, as follows:


More formally, the metric tensor can be expanded with respect to the coordinate cobasis as

A coframe can be read off from this expression:
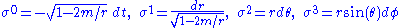
To see that this coframe really does correspond to the Schwarzschild metric tensor, just plug this coframe into
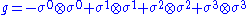
The frame dual to the coframe is
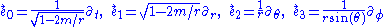
(The minus sign on
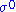 ensures that
ensures that 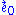 is future pointing.) This is the frame that models the experience of static observers who use rocket engines to "hover" over the massive object. The thrust they require to maintain their position is given by the magnitude of the acceleration vector
is future pointing.) This is the frame that models the experience of static observers who use rocket engines to "hover" over the massive object. The thrust they require to maintain their position is given by the magnitude of the acceleration vector
This is radially outward pointing, since the observers need to accelerate away from the object to avoid falling toward it. On the other hand, the spatially projected Fermi derivatives of the spatial basis vectors (with respect to
 ) vanish, so this is a nonspinning frame.
) vanish, so this is a nonspinning frame.The components of various tensorial quantities with respect to our frame and its dual coframe can now be computed.
For example, the tidal tensor
Electrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
for our static observers is defined using tensor notation (for a coordinate basis) as

where we write
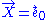 to avoid cluttering the notation. Its only non-zero components with respect to our coframe turn out to be
to avoid cluttering the notation. Its only non-zero components with respect to our coframe turn out to be
The corresponding coordinate basis components are

(A quick note concerning notation: many authors put caret
Caret
Caret usually refers to the spacing symbol ^ in ASCII and other character sets. In Unicode, however, the corresponding character is , whereas the Unicode character named caret is actually a similar but lowered symbol: ....
s over abstract indices referring to a frame. When writing down specific components, it is convenient to denote frame components by 0,1,2,3 and coordinate components by
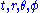 . Since an expression like
. Since an expression like  doesn't make sense as a tensor equation, there should be no possibility of confusion.)
doesn't make sense as a tensor equation, there should be no possibility of confusion.)Compare the tidal tensor
Tidal tensor
In Newton's theory of gravitation and in various relativistic classical theories of gravitation, such as general relativity, the tidal tensor represents#tidal accelerations of a cloud of test particles,...
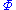 of Newtonian gravity, which is the traceless part of the Hessian
of Newtonian gravity, which is the traceless part of the HessianHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of the gravitational potential
 . Using tensor notation for a tensor field defined on three-dimensional euclidean space, this can be written
. Using tensor notation for a tensor field defined on three-dimensional euclidean space, this can be written
The reader may wish to crank this through (notice that the trace term actually vanishes identically when U is harmonic) and compare results with the following elementary approach:
we can compare the gravitational forces on two nearby observers lying on the same radial line:
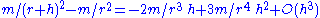
Because in discussing tensors we are dealing with multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, we retain only first order terms, so
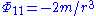 . Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere
. Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere  . Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
. Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
By using the small angle approximation, we have ignored all terms of order
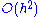 , so the tangential components are
, so the tangential components are 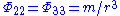 . Here, we are referring to the obvious frame obtained from the polar spherical chart for our three-dimensional euclidean space:
. Here, we are referring to the obvious frame obtained from the polar spherical chart for our three-dimensional euclidean space: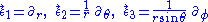
Plainly, the coordinate components
 computed above don't even scale the right way, so they clearly cannot correspond to what an observer will measure even approximately. (By coincidence, the Newtonian tidal tensor components agree exactly with the relativistic tidal tensor components we wrote out above.)
computed above don't even scale the right way, so they clearly cannot correspond to what an observer will measure even approximately. (By coincidence, the Newtonian tidal tensor components agree exactly with the relativistic tidal tensor components we wrote out above.)Example: Lemaître observers in the Schwarzschild vacuum
To find an inertial frame, we can boost our static frame in the direction by an undetermined boost parameter (depending on the radial coordinate), compute the acceleration vector of the new undetermined frame, set this equal to zero, and solve for the unknown boost parameter. The result will be a frame which we can use to study the physical experience of observers who fall freely and radially toward the massive object. By appropriately choosing an integration constant, we obtain the frame of Lemaître observers, who fall in from rest at spatial infinity. (This phrase doesn't make sense, but the reader will no doubt have no difficulty in understanding our meaning.) In the static polar spherical chart, this frame can be written
direction by an undetermined boost parameter (depending on the radial coordinate), compute the acceleration vector of the new undetermined frame, set this equal to zero, and solve for the unknown boost parameter. The result will be a frame which we can use to study the physical experience of observers who fall freely and radially toward the massive object. By appropriately choosing an integration constant, we obtain the frame of Lemaître observers, who fall in from rest at spatial infinity. (This phrase doesn't make sense, but the reader will no doubt have no difficulty in understanding our meaning.) In the static polar spherical chart, this frame can be written
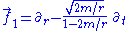
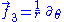

Note that
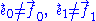 , and that
, and that 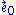 "leans inwards", as it should, since its integral curves are timelike geodesics representing the world lines of infalling observers. Indeed, since the covariant derivatives of all four basis vectors (taken with respect to
"leans inwards", as it should, since its integral curves are timelike geodesics representing the world lines of infalling observers. Indeed, since the covariant derivatives of all four basis vectors (taken with respect to  ) vanish identically, our new frame is a nonspinning inertial frame.
) vanish identically, our new frame is a nonspinning inertial frame.If our massive object is in fact a (nonrotating) black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, we probably wish to follow the experience of the Lemaître observers as they fall through the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
at
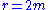 . Since the static polar spherical coordinates have a coordinate singularity at the horizon, we'll need to switch to a more appropriate coordinate chart. The simplest possible choice is to define a new time coordinate by
. Since the static polar spherical coordinates have a coordinate singularity at the horizon, we'll need to switch to a more appropriate coordinate chart. The simplest possible choice is to define a new time coordinate by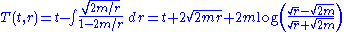
This gives the Painlevé chart
Gullstrand-Painlevé coordinates
Gullstrand–Painlevé coordinates were proposed by Paul Painlevé and Allvar Gullstrand in 1921. Similar to Schwarzschild coordinates, GP coordinates can be used in the Schwarzschild metric to describe the space-time physics outside the event horizon of a static black hole. However, Schwarzschild...
. The new line element is


With respect to the Painlevé chart, the Lemaître frame is




Notice that their spatial triad looks exactly like the frame for three-dimensional euclidean space which we mentioned above (when we computed the Newtonian tidal tensor). Indeed, the spatial hyperslices
 turn out to be locally isometric to flat three-dimensional euclidean space! (This is a remarkable and rather special property of the Schwarzschild vacuum; most spacetimes do not admit a slicing into flat spatial sections.)
turn out to be locally isometric to flat three-dimensional euclidean space! (This is a remarkable and rather special property of the Schwarzschild vacuum; most spacetimes do not admit a slicing into flat spatial sections.)The tidal tensor taken with respect to the Lemaître observers is

where we write
 to avoid cluttering the notation. This is a different tensor from the one we obtained above, because it is defined using a different family of observers. Nonetheless, its nonvanishing components look familiar:
to avoid cluttering the notation. This is a different tensor from the one we obtained above, because it is defined using a different family of observers. Nonetheless, its nonvanishing components look familiar:  . (This is again a rather special property of the Schwarzschild vacuum.)
. (This is again a rather special property of the Schwarzschild vacuum.)Notice that there is simply no way of defining static observers on or inside the event horizon. On the other hand, the Lemaître observers are not defined on the entire exterior region covered by the static polar spherical chart either, so in these examples, neither the Lemaître frame nor the static frame are defined on the entire manifold.
Example: Hagihara observers in the Schwarzschild vacuum
In the same way that we found the Lemaître observers, we can boost our static frame in the direction by an undetermined parameter (depending on the radial coordinate), compute the acceleration vector, and require that this vanish in the equatorial plane
direction by an undetermined parameter (depending on the radial coordinate), compute the acceleration vector, and require that this vanish in the equatorial plane  . The new Hagihara frame describes the physical experience of observers in stable circular orbits around our massive object. It was apparently first discussed by the distinguished (and mathematically gifted) astronomer Yusuke Hagihara
. The new Hagihara frame describes the physical experience of observers in stable circular orbits around our massive object. It was apparently first discussed by the distinguished (and mathematically gifted) astronomer Yusuke HagiharaYusuke Hagihara
was a Japanese astronomer noted for his contributions to celestial mechanics.Hagihara graduated from Tokyo Imperial University with a degree in astronomy in 1921 and became an assistant professor of astronomy there two years later. In 1923 the Japanese government sent him abroad as a traveling...
.
In the static polar spherical chart, the Hagihara frame is
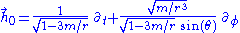
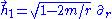
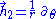
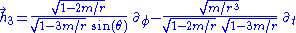
which in the equatorial plane becomes

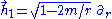

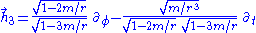
The tidal tensor
 where
where  turns out to be given (in the equatorial plane) by
turns out to be given (in the equatorial plane) by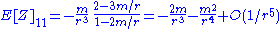
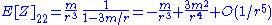

Thus, compared to a static observer hovering at a given coordinate radius,
a Hagihara observer in a stable circular orbit with the same coordinate radius will measure radial tidal forces which are slightly larger in magnitude, and transverse tidal forces which are no longer isotropic (but slightly larger orthogonal to the direction of motion).
Note that the Hagihara frame is only defined on the region
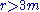 . Indeed, stable circular orbits only exist on
. Indeed, stable circular orbits only exist on 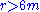 , so the frame should not be used inside this locus.
, so the frame should not be used inside this locus.Computing Fermi derivatives shows that the frame field just given is in fact spinning with respect to a gyrostabilized frame. The principal reason why is easy to spot: in this frame, each Hagihara observer keeps his spatial vectors radially aligned, so
 rotate about
rotate about 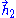 as the observer orbits around the central massive object. However, after correcting for this observation, a small precession of the spin axis of a gyroscope carried by a Hagihara observer still remains; this is the de Sitter precession effect (also called the geodetic precession effect).
as the observer orbits around the central massive object. However, after correcting for this observation, a small precession of the spin axis of a gyroscope carried by a Hagihara observer still remains; this is the de Sitter precession effect (also called the geodetic precession effect).Generalizations
This article has focused on the application of frames to general relativity, and particularly on their physical interpretation. Here we very briefly outline the general concept. In an n-dimensional Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, a frame field is a set of orthonormal vector fields which forms a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each point in the manifold. As before, frames can be specified in terms of a given coordinate basis, and in a non-flat region, some of their pairwise Lie brackets will fail to vanish.
In fact, given any inner-product space
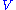 , we can define a new space consisting of all tuples of orthonormal bases for
, we can define a new space consisting of all tuples of orthonormal bases for 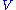 . Applying this construction to each tangent space yields the orthonormal frame bundle
. Applying this construction to each tangent space yields the orthonormal frame bundleFrame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of a (pseudo-)Riemannian manifold and a frame field is a section of this bundle. More generally still, we can consider frame bundles associated to any vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, or even arbitrary principal
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s. The notation becomes a bit more involved because it is harder to avoid distinguishing between indices referring to the base, and indices referring to the fiber. Many authors speak of internal components when referring to components indexed by the fiber.
See also
- Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
- Georges LemaîtreGeorges LemaîtreMonsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
- Karl SchwarzschildKarl SchwarzschildKarl Schwarzschild was a German physicist. He is also the father of astrophysicist Martin Schwarzschild.He is best known for providing the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-rotating mass, which he accomplished...
- Method of moving frames
- Paul PainlevéPaul PainlevéPaul Painlevé was a French mathematician and politician. He served twice as Prime Minister of the Third Republic: 12 September – 13 November 1917 and 17 April – 22 November 1925.-Early life:Painlevé was born in Paris....
- Vierbein
- Yusuke HagiharaYusuke Hagiharawas a Japanese astronomer noted for his contributions to celestial mechanics.Hagihara graduated from Tokyo Imperial University with a degree in astronomy in 1921 and became an assistant professor of astronomy there two years later. In 1923 the Japanese government sent him abroad as a traveling...

