Electrovacuum solution
Encyclopedia
In general relativity
, an electrovacuum solution (electrovacuum) is an exact solution
of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field
, which must satisfy the (curved-spacetime) source-free Maxwell equations appropriate to the given geometry. For this reason, electrovacuums are sometimes called (source-free) Einstein-Maxwell solutions.
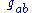(or by defining a frame field
). The curvature tensor
of this manifold and associated quantities such as the Einstein tensor
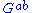, are well-defined even in the absence of any physical theory, but in general relativity they acquire a physical interpretation as geometric manifestations of the gravitational field
.
We also need to specify an electromagnetic field by defining an electromagnetic field tensor
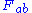on our Lorentzian manifold. These two tensors are required to satisfy two following conditions
The first Maxwell equation is satisfied automatically if we define the field tensor in terms of an electromagnetic potential vector
. In terms of the dual covector (or potential one-form) and the electromagnetic two-form, we can do this by setting 
. Then we need only ensure that the divergences vanish (i.e. that the second Maxwell equation is satisfied for a source-free field) and that the electromagnetic stress-energy matches the Einstein tensor.
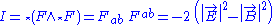
Using these, we can classify the possible electromagnetic fields as follows:
Null electrovacuums are associated with electromagnetic radiation. An electromagnetic field which is not null is called non-null, and then we have a non-null electrovacuum.
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the case of an electrovacuum solution, an adapted frame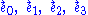
can always be found in which the Einstein tensor has a particularly simple appearance.
Here, the first vector is understood to be a timelike unit vector field; this is everywhere tangent to the world lines of the corresponding family of adapted observers, whose motion is "aligned" with the electromagnetic field. The last three are spacelike unit vector fields.
For a non-null electrovacuum, an adapted frame can be found in which the Einstein tensor takes the form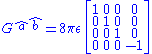
where
is the energy density of the electromagnetic field, as measured by any adapted observer. From this expression, it is easy to see that the isotropy group of our non-null electrovacuum is generated by boosts in the 
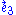direction and rotations about the 
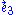axis. In other words, the isotropy group of any non-null electrovacuum is a two dimensional abelian Lie group
isomorphic to SO(1,1) x SO(2).
For a null electrovacuum, an adapted frame can be found in which the Einstein tensor takes the form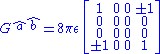
From this it is easy to see that the isotropy group of our null electrovacuum includes rotations about the
axis; two further generators are the two parabolic Lorentz transformations aligned with the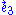 
direction given in the article on the Lorentz group
. In other words, the isotropy group of any null electrovacuum is a three dimensional Lie group isomorphic to E(2), the isometry group of the euclidean plane.
The fact that these results are exactly the same in curved spacetimes as for electrodynamics in flat Minkowski spacetime is one expression of the equivalence principle
.
of the Einstein tensor of an non-null electrovacuum must have the form
Using Newton's identities
, this condition can be re-expressed in terms of the trace
s of the powers of the Einstein tensor as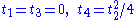
where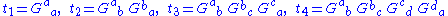
This necessary criterion can be useful for checking that a putative non-null electrovacuum solution is plausible, and is sometimes useful for finding non-null electrovacuum solutions.
The characteristic polynomial of a null electrovacuum vanishes identically, even if the energy density is nonzero. This possibility is a tensor analogue of the well known that a null vector always has vanishing length, even if it is not the zero vector. Thus, every null electrovacuum has one quadruple eigenvalue, namely zero.
presented purely mathematical conditions which are both necessary and sufficient for a Lorentzian manifold to admit an interpretation in general relativity as a non-null electrovacuum. These comprise three algebraic conditions and one differential condition. The conditions are sometimes useful for checking that a putative non-null electrovacuum really is what it claims, or even for finding such solutions.
No analogous necessary and sufficient conditions for a null electrovacuum are yet known, although some progress has been made.
. In this case, the electromagnetic field is often called a test field, in analogy with the term test particle
(denoting a small object whose mass is too small to contribute appreciably to the ambient gravitational field).
Here, it is useful to know that any Killing vectors which may be present will (in the case of a vacuum solution) automatically satisfy the curved spacetime Maxwell equations
.
Note that this procedure amounts to assuming that the electromagnetic field, but not the gravitational field, is "weak". Sometimes we can go even further; if the gravitational field is also considered "weak", we can independently solve the linearised Einstein field equations and the (flat spacetime) Maxwell equations on a Minkowksi vacuum background. Then the (weak) metric tensor gives the approximate geometry; the Minkowski background is unobservable by physical means, but mathematically much simpler to work with, whenever we can get away with such a sleight-of-hand.
Noteworthy individual null electrovacuum solutions include:
Some well known families of electrovacuums are:
Many pp-wave spacetimes admit an electromagnetic field tensor turning them into exact null electrovacuum solutions.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, an electrovacuum solution (electrovacuum) is an exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, which must satisfy the (curved-spacetime) source-free Maxwell equations appropriate to the given geometry. For this reason, electrovacuums are sometimes called (source-free) Einstein-Maxwell solutions.
Mathematical definition
In general relativity, the geometric setting for physical phenomena is a Lorentzian manifold, which is physically interpreted as a curved spacetime, and which is mathematically specified by defining a metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
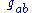(or by defining a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
). The curvature tensor
of this manifold and associated quantities such as the Einstein tensor
Einstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
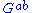, are well-defined even in the absence of any physical theory, but in general relativity they acquire a physical interpretation as geometric manifestations of the gravitational fieldGravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
.
We also need to specify an electromagnetic field by defining an electromagnetic field tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
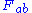on our Lorentzian manifold. These two tensors are required to satisfy two following conditions
- The electromagnetic field tensor must satisfy the source-free curved spacetime Maxwell field equations
and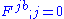 
- The Einstein tensor must match the electromagnetic stress-energy tensor,
.
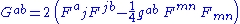The first Maxwell equation is satisfied automatically if we define the field tensor in terms of an electromagnetic potential vector
. In terms of the dual covector (or potential one-form) and the electromagnetic two-form, we can do this by setting . Then we need only ensure that the divergences vanish (i.e. that the second Maxwell equation is satisfied for a source-free field) and that the electromagnetic stress-energy matches the Einstein tensor.Invariants
As in flat spacetime, the electromagnetic field tensor is antisymmetric, with only two algebraically independent scalar invariants,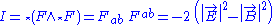Using these, we can classify the possible electromagnetic fields as follows:
- If
but 
, we have an electrostatic field, which means that some observers will measure a static electric field, and no magnetic field. - If
but 
, we have an magnetostatic field, which means that some observers will measure a static magnetic field, and no electric field. - If
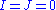, the electromagnetic field is said to be null, and we have a null electrovacuum.
Null electrovacuums are associated with electromagnetic radiation. An electromagnetic field which is not null is called non-null, and then we have a non-null electrovacuum.
Einstein tensor
The components of a tensor computed with respect to a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the case of an electrovacuum solution, an adapted frame
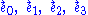
can always be found in which the Einstein tensor has a particularly simple appearance.
Here, the first vector is understood to be a timelike unit vector field; this is everywhere tangent to the world lines of the corresponding family of adapted observers, whose motion is "aligned" with the electromagnetic field. The last three are spacelike unit vector fields.
For a non-null electrovacuum, an adapted frame can be found in which the Einstein tensor takes the form
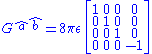
where
is the energy density of the electromagnetic field, as measured by any adapted observer. From this expression, it is easy to see that the isotropy group of our non-null electrovacuum is generated by boosts in the 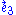direction and rotations about the 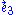axis. In other words, the isotropy group of any non-null electrovacuum is a two dimensional abelian Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
isomorphic to SO(1,1) x SO(2).
For a null electrovacuum, an adapted frame can be found in which the Einstein tensor takes the form
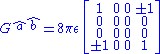
From this it is easy to see that the isotropy group of our null electrovacuum includes rotations about the
axis; two further generators are the two parabolic Lorentz transformations aligned with the 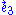direction given in the article on the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
. In other words, the isotropy group of any null electrovacuum is a three dimensional Lie group isomorphic to E(2), the isometry group of the euclidean plane.
The fact that these results are exactly the same in curved spacetimes as for electrodynamics in flat Minkowski spacetime is one expression of the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
.
Eigenvalues
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Einstein tensor of an non-null electrovacuum must have the form
Using Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, this condition can be re-expressed in terms of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
s of the powers of the Einstein tensor as
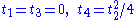
where
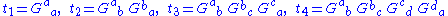
This necessary criterion can be useful for checking that a putative non-null electrovacuum solution is plausible, and is sometimes useful for finding non-null electrovacuum solutions.
The characteristic polynomial of a null electrovacuum vanishes identically, even if the energy density is nonzero. This possibility is a tensor analogue of the well known that a null vector always has vanishing length, even if it is not the zero vector. Thus, every null electrovacuum has one quadruple eigenvalue, namely zero.
Rainich conditions
In 1925, George Yuri RainichGeorge Yuri Rainich
George Yuri Rainich was a leading mathematical physicist in the early twentieth century.-Career:Rainich studied mathematics in Odessa and Munich, eventually obtaining his doctorate in 1913 from the University of Kazan...
presented purely mathematical conditions which are both necessary and sufficient for a Lorentzian manifold to admit an interpretation in general relativity as a non-null electrovacuum. These comprise three algebraic conditions and one differential condition. The conditions are sometimes useful for checking that a putative non-null electrovacuum really is what it claims, or even for finding such solutions.
No analogous necessary and sufficient conditions for a null electrovacuum are yet known, although some progress has been made.
Test fields
Sometimes one can assume that the field energy of any electromagnetic field is so small that its gravitational effects can be neglected. Then, to obtain an approximate electrovacuum solution, we need only solve the Maxwell equations on a given vacuum solutionVacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
. In this case, the electromagnetic field is often called a test field, in analogy with the term test particle
Test particle
In physical theories, a test particle is an idealized model of an object whose physical properties are assumed to be negligible except for the property being studied, which is considered to be insufficient to alter the behavior of the rest of the system...
(denoting a small object whose mass is too small to contribute appreciably to the ambient gravitational field).
Here, it is useful to know that any Killing vectors which may be present will (in the case of a vacuum solution) automatically satisfy the curved spacetime Maxwell equations
Maxwell's equations in curved spacetime
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system...
.
Note that this procedure amounts to assuming that the electromagnetic field, but not the gravitational field, is "weak". Sometimes we can go even further; if the gravitational field is also considered "weak", we can independently solve the linearised Einstein field equations and the (flat spacetime) Maxwell equations on a Minkowksi vacuum background. Then the (weak) metric tensor gives the approximate geometry; the Minkowski background is unobservable by physical means, but mathematically much simpler to work with, whenever we can get away with such a sleight-of-hand.
Examples
Noteworthy individual non-null electrovacuum solutions include:- Reissner–Nordström electrovacuum (which describes the geometry around a charged spherical mass),
- Kerr–Newman electrovacuum (which describes the geometry around a charged, rotating object),
- Melvin electrovacuum (a model of a cylindrically symmetric magnetostatic field),
- Garfinkle–Melvin electrovacuum (like the preceding, but including a gravitational wave traveling along the axis of symmetry),
- Bertotti–Robinson electrovacuum: this is a simple spacetime having a remarkable product structure; it arises from a kind of "blow up" of the horizon of the Reissner-Nordström electrovacuum,
- Witten electrovacuums (discovered by Louis WittenLouis WittenLouis Witten is an American theoretical physicist and the father of Edward Witten.Witten's research has centered around classical gravitation, including the discovery of certain exact electrovacuum solutions to the Einstein field equation...
, father of Edward WittenEdward WittenEdward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
).
Noteworthy individual null electrovacuum solutions include:
- the monochromatic electromagnetic plane waveMonochromatic electromagnetic plane waveIn general relativity, the monochromatic electromagnetic plane wave spacetime is the analog of the monochromatic plane waves known from Maxwell's theory...
, an exact solution which is the general relativitistic analogue of the plane waves in classical electromagnetism, - Bell–Szekeres electrovacuum (a colliding plane wave model).
Some well known families of electrovacuums are:
- Weyl–Maxwell electrovacuums: this is the family of all static axisymmetric electrovacuum solutions; it includes the Reissner-Nordström electrovacuum,
- Ernst–Maxwell electrovacuums: this is the family of all stationary axisymmetric electrovacuum solutions; it includes the Kerr-Newman electrovacuum,
- Beck–Maxwell electrovacuums: all nonrotating cylindrically symmetric electrovacuum solutions,
- Ehlers–Maxwell electrovacuums: all stationary cylindrically symmetric electrovacuum solutions,
- Szekeres electrovacuums: all pairs of colliding plane waves, where each wave may contain both gravitational and electromagnetic radiation; these solutions are null electrovacuums outside the interaction zone, but generally non-null electrovacuums inside the interaction zone, due to the non-linear interaction of the two waves after they collide.
Many pp-wave spacetimes admit an electromagnetic field tensor turning them into exact null electrovacuum solutions.
See also
- Classification of electromagnetic fieldsClassification of electromagnetic fieldsIn differential geometry and theoretical physics, the classification of electromagnetic fields is a pointwise classification of bivectors at each point of a Lorentzian manifold....
- Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
- Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...