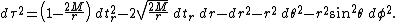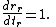
Gullstrand-Painlevé coordinates
Encyclopedia
Gullstrand–Painlevé coordinates were proposed by Paul Painlevé
and Allvar Gullstrand
in 1921. Similar to Schwarzschild coordinates
, GP coordinates can be used in the Schwarzschild metric
to describe the space-time physics outside the event horizon
of a static black hole
. However, Schwarzschild coordinates are only valid exterior to the event horizon
. GP coordinates were the first coordinates that could extend the analysis of space-time physics, such as the speed of particles and light, across the event horizon. The simplicity of the GP form makes it very useful for pedagogical purposes.
Convention: The units for the variables are all geometrized
. Time and mass have units in meters. The speed of light in flat spacetime has a value of 1. The gravitational constant has a value of 1.
The metric is expressed in the +−−− sign convention
.
, a free-float frame is the classic inertial frame which obeys Einstein's postulates of special relativity
. In general relativity
, it rides along the space-time geodesic
. The inside of an unpowered spaceship that plunges toward a nearby black hole demonstrates a typical free-float frame. The space-time in a free-float frame is flat and can be expressed by the metric (in the +−−− sign convention
):
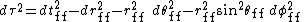
where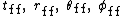
are the free-float coordinates and include spherical coordinates
.
The flatness claim is only locally valid. When space-time curvature increases, it may be necessary to decrease the dimensions of the frame so that the tidal acceleration
associated with the curvature is negligible.
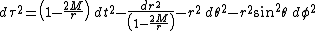
where
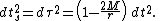
Take the square root:
Similarly, by considering two simultaneous events located in the same radial direction on two spherical shells separated by distance dr, the equation for drs can be derived:
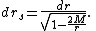
Locally, with the shell coordinates
, the metric for the shell frame is thus expressed in hybrid form:
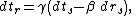
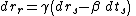
where
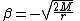
can be shown to be the velocity of the freely falling rain frame relative to the shell frame.
and
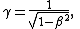
Taking into consideration the space-time curvature between the shell coordinates and the schwarzschild coordinates due to the presence of black hole, the rain coordinates can be derived:
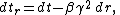
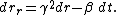
Substitute into the Schwarzschild form. The rain form is given by
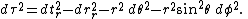
In Schwarzschild coordinates, the velocity of raindrop is given by
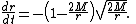
In GP coordinates, the velocity is given by
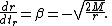
mathematically. Integrate the equation of motion:
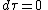. Therefore,
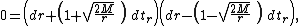
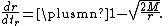
Paul Painlevé
Paul Painlevé was a French mathematician and politician. He served twice as Prime Minister of the Third Republic: 12 September – 13 November 1917 and 17 April – 22 November 1925.-Early life:Painlevé was born in Paris....
and Allvar Gullstrand
Allvar Gullstrand
Allvar Gullstrand was a Swedish ophthalmologist.Born at Landskrona, Sweden, Gullstrand was professor successively of eye therapy and of optics at the University of Uppsala. He applied the methods of physical mathematics to the study of optical images and of the refraction of light in the eye...
in 1921. Similar to Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, GP coordinates can be used in the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
to describe the space-time physics outside the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of a static black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. However, Schwarzschild coordinates are only valid exterior to the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
. GP coordinates were the first coordinates that could extend the analysis of space-time physics, such as the speed of particles and light, across the event horizon. The simplicity of the GP form makes it very useful for pedagogical purposes.
Derivation
The derivation of GP coordinates requires defining the following coordinate systems and understanding of how data measured for events in one coordinate system is interpreted in another coordinate system.Convention: The units for the variables are all geometrized
Geometrized unit system
A geometrized unit system or geometric unit system is a system of natural units in which the base physical units are chosen so that the speed of light in a vacuum, c, and the gravitational constant, G, are set equal to unity. c = 1 \ G = 1 \...
. Time and mass have units in meters. The speed of light in flat spacetime has a value of 1. The gravitational constant has a value of 1.
The metric is expressed in the +−−− sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
.
Free-float coordinates
In special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, a free-float frame is the classic inertial frame which obeys Einstein's postulates of special relativity
Postulates of special relativity
- Postulates of special relativity :1. First postulate 2. Second postulate - Alternate Derivations of Special Relativity :...
. In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, it rides along the space-time geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
. The inside of an unpowered spaceship that plunges toward a nearby black hole demonstrates a typical free-float frame. The space-time in a free-float frame is flat and can be expressed by the metric (in the +−−− sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
):
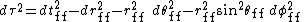
where
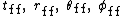are the free-float coordinates and include spherical coordinatesSpherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
.
The flatness claim is only locally valid. When space-time curvature increases, it may be necessary to decrease the dimensions of the frame so that the tidal acceleration
Tidal acceleration
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite , and the primary planet that it orbits . The "acceleration" is usually negative, as it causes a gradual slowing and recession of a satellite in a prograde orbit away from the primary, and a corresponding...
associated with the curvature is negligible.
Schwarzschild coordinates
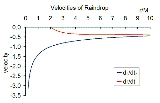
A Schwarzschild observer is a far observer or a bookkeeper. He does not directly make measurements of events that occur in different places. Instead, he is far away from the black hole and the events. Observers local to the events are enlisted to make measurements and send the results to him. The bookkeeper gathers and combines the reports from various places. The numbers in the reports are translated into data in Schwarzschild coordinates, which provide a systematic means of evaluating and describing the events globally. Thus, the physicist can compare and interpret the data intelligently. He can find meaningful information from these data. The Schwarzschild form of the Schwarzschild metric using Schwarzschild coordinates is given by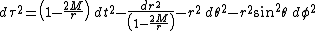where
- t, r, θ, φ are the Schwarzschild coordinates,
- M is the mass of the black hole.
Shell coordinates
Imagine a series of spherical shells held stationary against the force of gravity by rockets outside the event horizon. The shell observer, standing on the spherical shell, can form his own shell frame. When constricted to small enough region, the space-time in the shell frame can be regarded as flat. Special relativity works in the shell frame. Consider two sequential clicks of a clock at rest on a spherical shell, dr, dθ, dφ of the Schwarzschild coordinates is 0. Therefore, dts, the time coordinate in the shell frame is the proper time. Substitute into the Schwarzschild metric,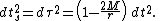Take the square root:
Similarly, by considering two simultaneous events located in the same radial direction on two spherical shells separated by distance dr, the equation for drs can be derived:
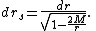
Locally, with the shell coordinates
, the metric for the shell frame is thus expressed in hybrid form:Rain coordinates
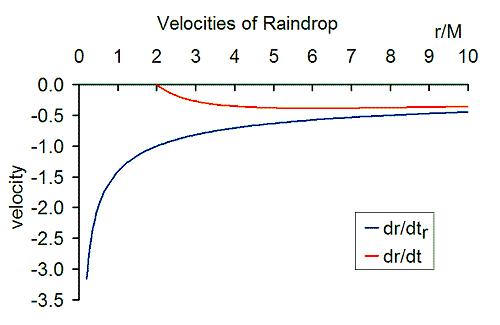
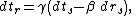
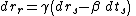
Define a rain frame as a free-float frame plunging radially and freely from rest at infinity toward a black hole. The time coordinate of the rain frame is obtained by Lorentz transformation from the shell coordinates outside the event horizon.where
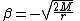
can be shown to be the velocity of the freely falling rain frame relative to the shell frame.
and
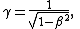
Taking into consideration the space-time curvature between the shell coordinates and the schwarzschild coordinates due to the presence of black hole, the rain coordinates can be derived:
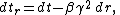
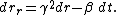
Substitute into the Schwarzschild form. The rain form is given by
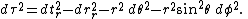
Gullstrand–Painlevé coordinates
When only dtr is plugged into the Schwarzschild form, the GP form is obtained
- The r-coordinate of Schwarzschild coordinates is used here. By using a mixed coordinate system, the GP form is able to interpret events globally.
- The GP form doesn't encounter the singularity at the event horizon, r = 2M. The r-coordinate term does not blow up at the event horizon. The only singularity is at the center of the black hole, r = 0. It's possible now to answer many more questions about static black holes.
Speeds of raindrop
Define a raindrop as an object which plunges radially toward a black hole from rest at infinity. A raindrop is at rest in a rain frame. Its velocity is also the relative velocity of the rain frame with respect to a shell observer and can be measured by the shell observer.In Schwarzschild coordinates, the velocity of raindrop is given by
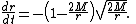
- The speed tends to 0 as r approaches the event horizon. The raindrop appears to have slowed as it gets nearer the event horizon and halted at the event horizon as measured by the bookkeeper. Indeed, an observer outside the event horizon would see the raindrop plunges slower and slower. Its images infinitely redshifted and never make it through the event horizon. However, the bookkeeper does not physically measure the speed directly. He translates data relayed by the shell observer into Schwarzschild values and compute the speed. The result is only an accounting entry.
In GP coordinates, the velocity is given by
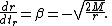
- The speed of the raindrop is inversely proportional to the square root of radius. At places very far away from the black hole, the speed is extremely small. As the raindrop plunges toward the black hold, the speed increases. At the event horizon, the speed has the value 1, same as the speed of light. There is no discontinuity or singularity at the event horizon.
- Inside the event horizon,
. The speed exceeds the speed of light. It increases as the raindrop gets ever more closer to the singularity. Eventually, the speed becomes infinite at the singularity. The results may not be correctly predicted by the equation at and near the singularity. The physics may be quite different when quantum mechanics is incorporated.
- Despite the problem with the singularity, it's still possible to compute the travel time for the raindrop from horizon to the center of black hole
mathematically. Integrate the equation of motion:
-
-
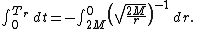The result is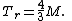 
-
Speeds of light
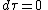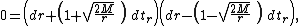
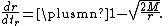
Assume radial motion. For light, . Therefore,- At places very far away from the black hole,
, 
. The speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is 1, the same as in special relativity.
- At the event horizon,
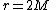, the speed of light shining outward away from the center of black hole is 
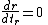. It can not escape from the event horizon. Instead, it gets stuck at the event horizon. Since light moves faster than all others, matter can only move inward at the event horizon. Everything inside the event horizon is hidden from the outside world.
- Inside the event horizon, r < 2M, the rain observer measures that the light moves toward the center with speed greater than 2. This is plausible. Even in special relativity, the proper speed of a moving object is
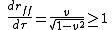. There are 2 important points to consider:
-
- No object should have speed greater than the speed of light as measured in the same reference frame. Thus, the principle of causality is preserved. Indeed, the speed of raindrop is less than that of light:
.
-
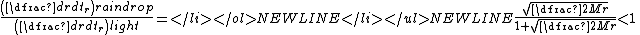- Universally, there can be only one value for the speed of light in the free-float frame and it should be 1. The rain frame is a free-float frame which works inside the event horizon. Indeed, the speed of light in the rain frame is
- The time of travel for light shining inward from event horizon to the center of black hole can be obtained by integrating the equation for the velocity of light,
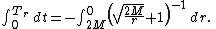The result is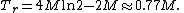 
- The light travel time for a stellar black holeStellar black holeA stellar black hole is a black hole formed by the gravitational collapse of a massive star. They have masses ranging from about 3 to several tens of solar masses...
with a typical size of 3 solar masses is about 11 microseconds. - Ignoring effects of rotation, for Sagittarius A*, the supermassive black holeSupermassive black holeA supermassive black hole is the largest type of black hole in a galaxy, in the order of hundreds of thousands to billions of solar masses. Most, and possibly all galaxies, including the Milky Way, are believed to contain supermassive black holes at their centers.Supermassive black holes have...
residing at the center of the Milky WayMilky WayThe Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
, with mass of 3.7 million solar masses, the light travel time is about 14 seconds. - The supermassive black hole at the center of Messier 87Messier 87Messier 87 is a supergiant elliptical galaxy. It was discovered in 1781 by the French astronomer Charles Messier, who cataloged it as a nebulous feature. The second brightest galaxy within the northern Virgo Cluster, it is located about 16.4 million parsecs from Earth...
, a giant elliptical galaxy in the Virgo ClusterVirgo ClusterThe Virgo Cluster is a cluster of galaxies whose center is 53.8 ± 0.3 Mly away in the constellation Virgo. Comprising approximately 1300 member galaxies, the cluster forms the heart of the larger Local Supercluster, of which the Local Group is an outlying member...
, is the biggest known black hole. It has a mass of approximately 3 billion solar masses. It would take about 3 hours for light to travel to the central singularity of such a supermassive black hole, and for raindrop, 5 hours.
- The light travel time for a stellar black hole
A rain observer's view of the universe
How does the universe look like as seen by a rain observer plunging into the black hole? The view can be described by the following equations: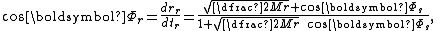
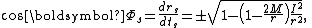
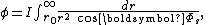
where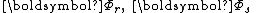
are the rain observer's and shell observer's viewing angles with respect to the radially outward direction.
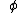is the angle between the distant star and the radially outward direction.
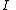is the impact parameter. Each incoming light ray can be backtraced to a corresponding ray at infinity. The Impact parameter for the incoming light ray is the distance between the corresponding ray at infinity and a ray parallel to it that plunges directly into the black hole.
Because of spherical symmetry, the trajectory of light always lies in a plane passing through the center of sphere. It's possible to simplify the metric by assuming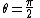
.
The impact parameter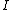
can be computed knowing the rain observer's r-coordinate 
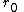and viewing angle 
. Then, the actual angle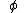 
of the distant star, is determined by numerically integrating 
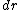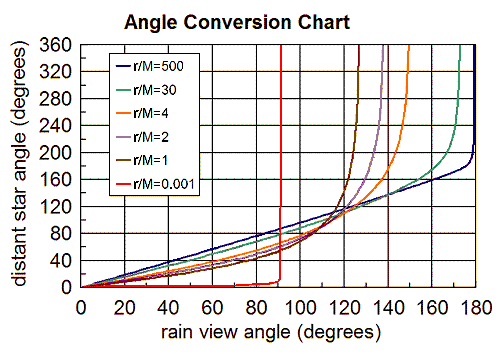
from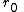 
to infinity. A chart of the sample results is shown at right.
- At r/M = 500, the black hole is still very far away. It subtends a diametrical angle of ~ 1 degree in the sky. The stars are not distorted much by the presence of the black hole, except for the stars directly behind it. Due to gravitiational lensing, These obstructed stars are now deflected 5 degrees away from the back. In between these stars and the black hole is a circular band of secondary images of the stars. The duplicate images are instrumental in the identification of the black hole.
- At r/M = 30, the black hole has become much bigger, spanning a diametrical angle of ~15 degrees in the sky. The band of secondary images has also grown to 10 degrees. It’s now possible to find faint tertiary images in the band, which are produced by the light rays that have looped around the black hole once already. The primary images are distributed more tightly in the rest of the sky. The pattern of distribution is similar to that previously exhibited.
- At r/M = 2, the event horizon, the black hole now occupies a substantial portion of the sky. The rain observer would see an area up to 42 degrees from the radially inward direction that is pitch dark. The band of secondary and tertiary images, rather than increasing, has decreased in size to 5 degrees. The aberration effectAberration of lightThe aberration of light is an astronomical phenomenon which produces an apparent motion of celestial objects about their real locations...
is now quite dominant. The speed of plunging has reached the light speed. The distribution pattern of primary images is changing drastically. The primary images are shifting toward the boundary of the band. The edge near the band is now crowded with stars. Due to Doppler effectDoppler effectThe Doppler effect , named after Austrian physicist Christian Doppler who proposed it in 1842 in Prague, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from...
, the stars which were originally located behind the rain observer have their images appreciably red-shifted, while those in front are blue-shifted and appear very bright.
- At r/M=0.001, the curve of distant star angle versus view angle appears to form a right angle at the 90 degrees view anagle. Almost all of the star images are congregated in a narrow ring 90 degrees from the radially inward direction. Between the ring and the radially inward direction is the enormous black hole. On the opposite side, only a few stars shine faintly.
- As the rain observer approaches the singularity,
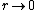, and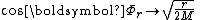 
. Most of the stars are squeezed to a narrow band at the 90° viewing angle. The observer sees a magnificent bright ring of stars bisecting the dark sky.
See also
- Isotropic coordinatesIsotropic coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often...
- Eddington–Finkelstein coordinates
- Kruskal–Szekeres coordinates
External links
-
- No object should have speed greater than the speed of light as measured in the same reference frame. Thus, the principle of causality is preserved. Indeed, the speed of raindrop is less than that of light:
