
Tidal tensor
Encyclopedia
In Newton's theory of gravitation and in various relativistic classical theories of gravitation
, such as general relativity
, the tidal tensor represents
 , which obeys the Poisson equation
, which obeys the Poisson equation
where is the mass density of any matter present. Note that this equation implies that in a vacuum solution
is the mass density of any matter present. Note that this equation implies that in a vacuum solution
, the potential is simply a harmonic function
.
The tidal tensor is given by the traceless part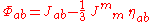
of the Hessian
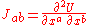
where we are using the standard Cartesian chart for E3, with the Euclidean metric tensor
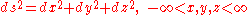
Using standard results in vector calculus, this is readily converted to expressions valid in other coordinate charts, such as the polar spherical chart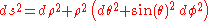

Let us adopt the frame obtained from the polar spherical chart for our three-dimensional Euclidean space: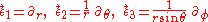
We will directly compute the tidal tensor, expressed in this frame, by elementary means, as follows.
First, compare the gravitational forces on two nearby observers lying on the same radial line: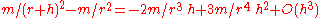
Because in discussing tensors we are dealing with multilinear algebra
, we retain only first order terms, so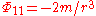 . Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere
. Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere 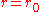 . Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
. Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude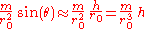
By using the small angle approximation, we have ignored all terms of order , so the tangential components are
, so the tangential components are 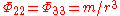 . Combining this information, we find that the tidal tensor is diagonal with frame components
. Combining this information, we find that the tidal tensor is diagonal with frame components
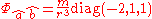
This is the Coulomb form characteristic of spherically symmetric central force fields in Newtonian physics.
Next, let us plug the gravitational potential into the Hessian. We can convert the expression above to one valid in polar spherical coordinates, or we can convert the potential to Cartesian coordinates before plugging in. Adopting the second course, we have
into the Hessian. We can convert the expression above to one valid in polar spherical coordinates, or we can convert the potential to Cartesian coordinates before plugging in. Adopting the second course, we have 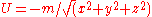 , which gives
, which gives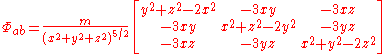
After a rotation of our frame, which is adapted to the polar spherical coordinates, this expression agrees with our previous result. (The easiest way to see this is probably to set y,z to zero so that the off-diagonal terms vanish and , and then invoke the spherical symmetry.)
, and then invoke the spherical symmetry.)
, which is one piece of the Bel decomposition
of the Riemann tensor.
Classical theories of gravitation
The current Gold Standard Theory of Gravitation is the general theory of relativity. This is a classical, relativistic field theory of gravitation...
, such as general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the tidal tensor represents
- tidal accelerations of a cloud of (electrically neutral, nonspinning) test particleTest particleIn physical theories, a test particle is an idealized model of an object whose physical properties are assumed to be negligible except for the property being studied, which is considered to be insufficient to alter the behavior of the rest of the system...
s, - tidal stresses in a small object immersed in an ambient gravitational field.
Newton's theory
In the field theoretic elaboration of Newtonian gravity, the central quantity is the gravitational potential , which obeys the Poisson equation
, which obeys the Poisson equation
where
 is the mass density of any matter present. Note that this equation implies that in a vacuum solution
is the mass density of any matter present. Note that this equation implies that in a vacuum solutionVacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
, the potential is simply a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
.
The tidal tensor is given by the traceless part
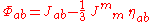
of the Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
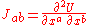
where we are using the standard Cartesian chart for E3, with the Euclidean metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
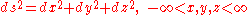
Using standard results in vector calculus, this is readily converted to expressions valid in other coordinate charts, such as the polar spherical chart
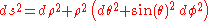

Spherically symmetric field
As an example, we compute the tidal tensor for the vacuum field outside an isolated spherically symmetric massive object in two different ways.Let us adopt the frame obtained from the polar spherical chart for our three-dimensional Euclidean space:
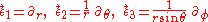
We will directly compute the tidal tensor, expressed in this frame, by elementary means, as follows.
First, compare the gravitational forces on two nearby observers lying on the same radial line:
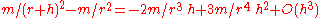
Because in discussing tensors we are dealing with multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, we retain only first order terms, so
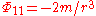 . Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere
. Similarly, we can compare the gravitational force on two nearby observers lying on the same sphere 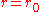 . Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude
. Using some elementary trigonometry and the small angle approximation, we find that the force vectors differ by a vector tangent to the sphere which has magnitude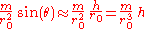
By using the small angle approximation, we have ignored all terms of order
 , so the tangential components are
, so the tangential components are 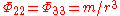 . Combining this information, we find that the tidal tensor is diagonal with frame components
. Combining this information, we find that the tidal tensor is diagonal with frame components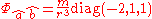
This is the Coulomb form characteristic of spherically symmetric central force fields in Newtonian physics.
Next, let us plug the gravitational potential
 into the Hessian. We can convert the expression above to one valid in polar spherical coordinates, or we can convert the potential to Cartesian coordinates before plugging in. Adopting the second course, we have
into the Hessian. We can convert the expression above to one valid in polar spherical coordinates, or we can convert the potential to Cartesian coordinates before plugging in. Adopting the second course, we have 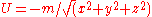 , which gives
, which gives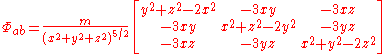
After a rotation of our frame, which is adapted to the polar spherical coordinates, this expression agrees with our previous result. (The easiest way to see this is probably to set y,z to zero so that the off-diagonal terms vanish and
 , and then invoke the spherical symmetry.)
, and then invoke the spherical symmetry.)General relativity
In general relativity, the tidal tensor is identified with the electrogravitic tensorElectrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
, which is one piece of the Bel decomposition
Bel decomposition
In semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann tensor.

