
Congruence (general relativity)
Encyclopedia
In general relativity
, a congruence (more properly, a congruence of curves) is the set of integral curve
s of a (nowhere vanishing) vector field
in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime
. Often this manifold will be taken to be an exact
or approximate solution to the Einstein field equation.
A congruence is called a geodesic congruence if the tangent vector field has vanishing covariant derivative
has vanishing covariant derivative
, .
.
Many distinct vector fields can give rise to the same congruence of curves, since if is a nowhere vanishing scalar function, then
is a nowhere vanishing scalar function, then  and
and  give rise to the same congruence.
give rise to the same congruence.
However, in a Lorentzian manifold, we have a metric tensor
, which picks out a preferred vector field among the vector fields which are everywhere parallel to a given timelike or spacelike vector field, namely the field of tangent vector
s to the curves. These are respectively timelike or spacelike unit vector fields.
s of certain ideal observers in our spacetime. In particular, a timelike geodesic congruence can be interpreted as a family of free-falling test particles.
Null congruences are also important, particularly null geodesic congruences, which can be interpreted as a family of freely propagating light rays.
Warning: the world line of a pulse of light moving in a fiber optic cable would not in general be a null geodesic, and light in the very early universe (the radiation-dominated epoch) was not freely propagating. The world line of a radar pulse sent from Earth
past the Sun
to Venus
would however be modeled as a null geodesic arc.
or FRW dust is a very important problem in general relativity. It is solved by defining certain kinematical quantities which completely describe how the integral curves in a congruence may converge (diverge) or twist about one another.
It should be stressed that the kinematical decomposition we are about to describe is pure mathematics valid for any Lorentzian manifold. However, the physical interpretation in terms of test particles and tidal accelerations (for timelike geodesic congruences) or pencils of light rays (for null geodesic congruences) is valid only for general relativity (similar interpretations may be valid in closely related theories).
X, which we should think of as a first order linear partial differential operator. Then the components of our vector field are now scalar functions given in tensor notation by writing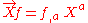 , where f is an arbitrary smooth function.
, where f is an arbitrary smooth function.
The acceleration vector is the covariant derivative
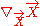 ; we can write its components in tensor notation as
; we can write its components in tensor notation as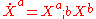
Next, observe that the equation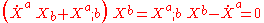
means that the term in parentheses at left is the transverse part of .Note that this orthogonality relation holds only when X is a timelike unit vector of a Lorenzian Manifold. It does not hold in more general setting. Write
.Note that this orthogonality relation holds only when X is a timelike unit vector of a Lorenzian Manifold. It does not hold in more general setting. Write
for the projection tensor which projects tensors into their transverse parts; for example, the transverse part of a vector is the part orthogonal to . This tensor can be seen as the metric tensor of the hypersurface whose tangent vectors are orthogonal to X. Thus we have shown that
. This tensor can be seen as the metric tensor of the hypersurface whose tangent vectors are orthogonal to X. Thus we have shown that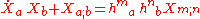
Next, we decompose this into its symmetric and antisymmetric parts,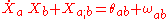
Here,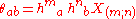

are known as the expansion tensor and vorticity tensor respectively.
Because these tensors live in the spatial hyperplane elements orthogonal to , we may think of them as three-dimensional second rank tensors. This can be expressed more rigorously using the notion of Fermi Derivative. Therefore we can decompose the expansion tensor into its traceless part plus a the trace part. Writing the trace as
, we may think of them as three-dimensional second rank tensors. This can be expressed more rigorously using the notion of Fermi Derivative. Therefore we can decompose the expansion tensor into its traceless part plus a the trace part. Writing the trace as  , we have
, we have
Because the vorticity tensor is antisymmetric, its diagonal components vanish, so it is automatically traceless (and we can replace it with a three-dimensional vector, although we shall not do this). Therefore we now have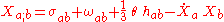
This is the desired kinematical decomposition. In the case of a timelike geodesic congruence, the last term vanishes identically.
The expansion scalar, shear tensor ( ), and vorticity tensor of a timelike geodesic congruence have the following intuitive meaning:
), and vorticity tensor of a timelike geodesic congruence have the following intuitive meaning:
See the citations and links below for justification of these claims.
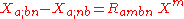
By plugging the kinematical decomposition into the left hand side, we can establish relations between the curvature tensor and the kinematical behavior of timelike congruences (geodesic or not). These relations can be used in two ways, both very important:
In the famous slogan of John Archibald Wheeler
,
We now see how to precisely quantify the first part of this assertion; the Einstein field equation quantifies the second part.
In particular, according to the Bel decomposition
of the Riemann tensor, taken with respect to our timelike unit vector field, the electrogravitic tensor
(or tidal tensor) is defined by
The Ricci identity now gives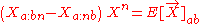
Plugging in the kinematical decomposition we can eventually obtain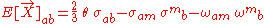
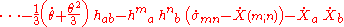
Here, overdots denote differentiation with respect to proper time, counted off along our timelike congruence (i.e. we take the covariant derivative with respect to the vector field X). This can be regarded as a description of how one can determine the tidal tensor from observations of a single timelike congruence.
It will be convenient to write the acceleration vector as and also to set
and also to set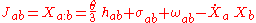
Now from the Ricci identity for the tidal tensor we have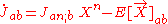
But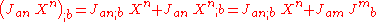
so we have
By plugging in the definition of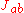 and taking respectively the diagonal part, the traceless symmetric part, and the antisymmetric part of this equation, we obtain the desired evolution equations for the expansion scalar, the shear tensor, and the vorticity tensor.
and taking respectively the diagonal part, the traceless symmetric part, and the antisymmetric part of this equation, we obtain the desired evolution equations for the expansion scalar, the shear tensor, and the vorticity tensor.
Let us consider first the easier case when the acceleration vector vanishes. Then (observing that the projection tensor can be used to lower indices of purely spatial quantities), we have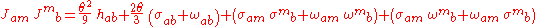
or
By elementary linear algebra, it is easily verified that if are respectively three dimensional symmetric and antisymmetric linear operators, then
are respectively three dimensional symmetric and antisymmetric linear operators, then  is symmetric while
is symmetric while  is antisymmetric, so by lowering an index, the corresponding combinations in parentheses above are symmetric and antisymmetric respectively. Therefore, taking the trace gives Raychaudhuri's equation (for timelike geodesics):
is antisymmetric, so by lowering an index, the corresponding combinations in parentheses above are symmetric and antisymmetric respectively. Therefore, taking the trace gives Raychaudhuri's equation (for timelike geodesics):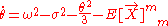
Taking the traceless symmetric part gives
and taking the antisymmetric part gives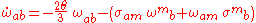
Here,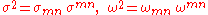
are quadratic invariants which are never negative, so that are well-defined real invariants. Note too that the trace of the tidal tensor can also be written
are well-defined real invariants. Note too that the trace of the tidal tensor can also be written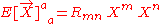
It is sometimes called the Raychaudhuri scalar; needless to say, it vanishes identically in the case of a vacuum solution
.
ἌἃὌῬῥὝῲψΨ
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a congruence (more properly, a congruence of curves) is the set of integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of a (nowhere vanishing) vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Often this manifold will be taken to be an exact
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
or approximate solution to the Einstein field equation.
Types of congruences
Congruences generated by nowhere vanishing timelike, null, or spacelike vector fields are called timelike, null, or spacelike respectively.A congruence is called a geodesic congruence if the tangent vector field
 has vanishing covariant derivative
has vanishing covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
,
 .
.Relation with vector fields
The integral curves of the vector field are a family of non-intersecting parameterized curves which fill up the spacetime. The congruence consists of the curves themselves, without reference to a particular parameterization.Many distinct vector fields can give rise to the same congruence of curves, since if
 is a nowhere vanishing scalar function, then
is a nowhere vanishing scalar function, then  and
and  give rise to the same congruence.
give rise to the same congruence.However, in a Lorentzian manifold, we have a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, which picks out a preferred vector field among the vector fields which are everywhere parallel to a given timelike or spacelike vector field, namely the field of tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s to the curves. These are respectively timelike or spacelike unit vector fields.
Physical interpretation
In general relativity, a timelike congruence in a four-dimensional Lorentzian manifold can be interpreted as a family of world lineWorld line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s of certain ideal observers in our spacetime. In particular, a timelike geodesic congruence can be interpreted as a family of free-falling test particles.
Null congruences are also important, particularly null geodesic congruences, which can be interpreted as a family of freely propagating light rays.
Warning: the world line of a pulse of light moving in a fiber optic cable would not in general be a null geodesic, and light in the very early universe (the radiation-dominated epoch) was not freely propagating. The world line of a radar pulse sent from Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
past the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
to Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
would however be modeled as a null geodesic arc.
Kinematical description
Describing the mutual motion of the test particles in a null geodesic congruence in a spacetime such as the Schwarzschild vacuumSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
or FRW dust is a very important problem in general relativity. It is solved by defining certain kinematical quantities which completely describe how the integral curves in a congruence may converge (diverge) or twist about one another.
It should be stressed that the kinematical decomposition we are about to describe is pure mathematics valid for any Lorentzian manifold. However, the physical interpretation in terms of test particles and tidal accelerations (for timelike geodesic congruences) or pencils of light rays (for null geodesic congruences) is valid only for general relativity (similar interpretations may be valid in closely related theories).
The kinematical decomposition of a timelike congruence
Consider the timelike congruence generated by some timelike unit vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X, which we should think of as a first order linear partial differential operator. Then the components of our vector field are now scalar functions given in tensor notation by writing
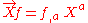 , where f is an arbitrary smooth function.
, where f is an arbitrary smooth function.The acceleration vector is the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
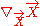 ; we can write its components in tensor notation as
; we can write its components in tensor notation as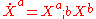
Next, observe that the equation
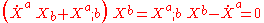
means that the term in parentheses at left is the transverse part of
 .Note that this orthogonality relation holds only when X is a timelike unit vector of a Lorenzian Manifold. It does not hold in more general setting. Write
.Note that this orthogonality relation holds only when X is a timelike unit vector of a Lorenzian Manifold. It does not hold in more general setting. Write
for the projection tensor which projects tensors into their transverse parts; for example, the transverse part of a vector is the part orthogonal to
 . This tensor can be seen as the metric tensor of the hypersurface whose tangent vectors are orthogonal to X. Thus we have shown that
. This tensor can be seen as the metric tensor of the hypersurface whose tangent vectors are orthogonal to X. Thus we have shown that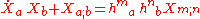
Next, we decompose this into its symmetric and antisymmetric parts,
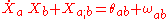
Here,
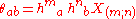

are known as the expansion tensor and vorticity tensor respectively.
Because these tensors live in the spatial hyperplane elements orthogonal to
 , we may think of them as three-dimensional second rank tensors. This can be expressed more rigorously using the notion of Fermi Derivative. Therefore we can decompose the expansion tensor into its traceless part plus a the trace part. Writing the trace as
, we may think of them as three-dimensional second rank tensors. This can be expressed more rigorously using the notion of Fermi Derivative. Therefore we can decompose the expansion tensor into its traceless part plus a the trace part. Writing the trace as  , we have
, we have
Because the vorticity tensor is antisymmetric, its diagonal components vanish, so it is automatically traceless (and we can replace it with a three-dimensional vector, although we shall not do this). Therefore we now have
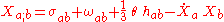
This is the desired kinematical decomposition. In the case of a timelike geodesic congruence, the last term vanishes identically.
The expansion scalar, shear tensor (
 ), and vorticity tensor of a timelike geodesic congruence have the following intuitive meaning:
), and vorticity tensor of a timelike geodesic congruence have the following intuitive meaning:
- the expansion scalar represents the fractional rate at which the volume of a small initially spherical cloud of test particles changes with respect to proper time of the particle at the center of the cloud,
- the shear tensor represents any tendency of the initial sphere to become distorted into an ellipsoidal shape,
- the vorticity tensor represents any tendency of the initial sphere to rotate; the vorticity vanishes if and only if the world lines in the congruence are everywhere orthogonal to the spatial hypersurfaces in some foliationFoliationIn mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of the spacetime, in which case, for a suitable coordinate chart, each hyperslice can be considered as a surface of 'constant time'.
See the citations and links below for justification of these claims.
Curvature and timelike congruences
By the Ricci identity (which is often used as the definition of the Riemann tensor), we can write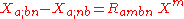
By plugging the kinematical decomposition into the left hand side, we can establish relations between the curvature tensor and the kinematical behavior of timelike congruences (geodesic or not). These relations can be used in two ways, both very important:
- we can (in principle) experimentally determine the curvature tensor of a spacetime from detailed observations of the kinematical behavior of any timelike congruence (geodesic or not),
- we can obtain evolution equations for the pieces of the kinematical decomposition (expansion scalar, shear tensor, and vorticity tensor) which exhibit direct curvature coupling.
In the famous slogan of John Archibald Wheeler
John Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
,
Spacetime tells matter how to move; matter tells spacetime how to curve.
We now see how to precisely quantify the first part of this assertion; the Einstein field equation quantifies the second part.
In particular, according to the Bel decomposition
Bel decomposition
In semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann tensor, taken with respect to our timelike unit vector field, the electrogravitic tensor
Electrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
(or tidal tensor) is defined by

The Ricci identity now gives
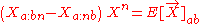
Plugging in the kinematical decomposition we can eventually obtain
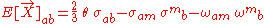
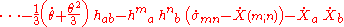
Here, overdots denote differentiation with respect to proper time, counted off along our timelike congruence (i.e. we take the covariant derivative with respect to the vector field X). This can be regarded as a description of how one can determine the tidal tensor from observations of a single timelike congruence.
Evolution equations
In this section, we turn to the problem of obtaining evolution equations (also called propagation equations or propagation formulae).It will be convenient to write the acceleration vector as
 and also to set
and also to set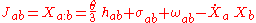
Now from the Ricci identity for the tidal tensor we have
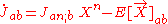
But
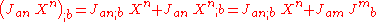
so we have

By plugging in the definition of
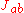 and taking respectively the diagonal part, the traceless symmetric part, and the antisymmetric part of this equation, we obtain the desired evolution equations for the expansion scalar, the shear tensor, and the vorticity tensor.
and taking respectively the diagonal part, the traceless symmetric part, and the antisymmetric part of this equation, we obtain the desired evolution equations for the expansion scalar, the shear tensor, and the vorticity tensor.Let us consider first the easier case when the acceleration vector vanishes. Then (observing that the projection tensor can be used to lower indices of purely spatial quantities), we have
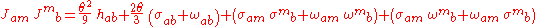
or

By elementary linear algebra, it is easily verified that if
 are respectively three dimensional symmetric and antisymmetric linear operators, then
are respectively three dimensional symmetric and antisymmetric linear operators, then  is symmetric while
is symmetric while  is antisymmetric, so by lowering an index, the corresponding combinations in parentheses above are symmetric and antisymmetric respectively. Therefore, taking the trace gives Raychaudhuri's equation (for timelike geodesics):
is antisymmetric, so by lowering an index, the corresponding combinations in parentheses above are symmetric and antisymmetric respectively. Therefore, taking the trace gives Raychaudhuri's equation (for timelike geodesics):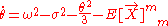
Taking the traceless symmetric part gives

and taking the antisymmetric part gives
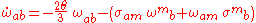
Here,
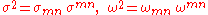
are quadratic invariants which are never negative, so that
 are well-defined real invariants. Note too that the trace of the tidal tensor can also be written
are well-defined real invariants. Note too that the trace of the tidal tensor can also be written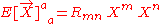
It is sometimes called the Raychaudhuri scalar; needless to say, it vanishes identically in the case of a vacuum solution
Vacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
.
ἌἃὌῬῥὝῲψΨ
See also
- congruence (manifolds)Congruence (manifolds)In the theory of smooth manifolds, a congruence is the set of integral curves defined by a nonvanishing vector field defined on the manifold.Congruences are an important concept in general relativity, and are also important in parts of Riemannian geometry....
- expansion scalar
- expansion tensor
- shear tensor
- vorticity tensor
- Raychaudhuri's equation

