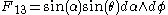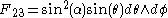Tetrad (index notation)
Encyclopedia
In Riemannian geometry
, we can introduce a coordinate system
over the Riemannian manifold
(at least, over a chart), giving n coordinates
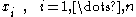
for an n-dimensional manifold. Locally, at least, this gives a basis for the 1-forms, dxi where d is the exterior derivative
. The dual basis for the tangent space
T is ei.
Now, let's choose an orthonormal basis
for the fibers
of T. The rest is index manipulation.
with the radius
R and give it polar coordinates α, θ, φ.
form an orthonormal basis of T.
Call these e1, e2 and e3. Given the metric η, we can ignore the covariant and contravariant distinction for T.
Then, the dreibein,
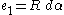
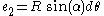
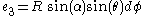 .
.
So,
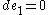

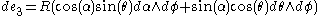 .
.
from the relation
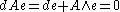 ,
,
we get
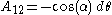
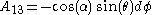
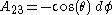 .
.
(dAη=0 tells us A is antisymmetric)
So, ,
,

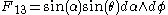
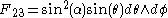
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, we can introduce a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
over the Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(at least, over a chart), giving n coordinates
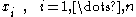
for an n-dimensional manifold. Locally, at least, this gives a basis for the 1-forms, dxi where d is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
. The dual basis for the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
T is ei.
Now, let's choose an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for the fibers
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of T. The rest is index manipulation.
Example
Take a 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
with the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
R and give it polar coordinates α, θ, φ.
- e(eα)/R,
- e(eθ)/R sin(α) and
- e(eφ)/R sin(α) sin(θ)
form an orthonormal basis of T.
Call these e1, e2 and e3. Given the metric η, we can ignore the covariant and contravariant distinction for T.
Then, the dreibein,
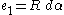
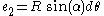
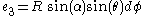 .
.So,
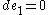

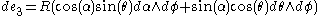 .
.from the relation
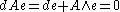 ,
,we get
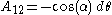
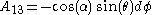
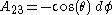 .
.(dAη=0 tells us A is antisymmetric)
So,
 ,
,