Schwarzschild metric
Encyclopedia
In Einstein
's theory of general relativity
, the Schwarzschild solution (or the Schwarzschild vacuum) describes the gravitational field
outside a spherical, uncharged
, non-rotating mass such as a (non-rotating) star
, planet
, or black hole
. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth
or Sun
. The cosmological constant
is assumed to equal zero.
According to Birkhoff's theorem
, the Schwarzschild solution is the most general spherically symmetric
, vacuum solution
of the Einstein field equations
. A Schwarzschild black hole or static black hole is a black hole
that has no charge
or angular momentum
. A Schwarzschild black hole has a Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.
The Schwarzschild black hole is characterized by a surrounding spherical surface, called the event horizon
, which is situated at the Schwarzschild radius
, often called the radius of a black hole. Any non-rotating and non-charged mass that is smaller than its Schwarzschild radius forms a black hole. The solution of the Einstein field equations is valid for any mass M, so in principle (according to general relativity
theory) a Schwarzschild black hole of any mass could exist if conditions became sufficiently favorable to allow for its formation.
, who found the exact solution in 1915, only about a month after the publication of Einstein's theory of general relativity. It was the first exact solution
of the Einstein field equations other than the trivial flat space solution. Schwarzschild had little time to think about his solution. He died shortly after his paper was published, as a result of a disease he contracted while serving in the German army during World War I
.
Johannes Droste in 1915
independently produced the same solution as Schwarzschild, using a simpler more direct derivation.
In the early years of general relativity there was a lot of confusion about the nature of the singularities found in the Schwarzschild and other solutions of the Einstein field equations
. In his 1916 paper Schwarzschild took the position that the singularity at r = rs should be identified with the coordinate singularity at the origin present in spherical coordinates on flat space. A more complete analysis of the singularity structure was given by David Hilbert
in the following year, identifying the singularities both at r = 0 and r = rs. Although there was general consent that the singularity at r = 0 was 'genuine' physical singularity, the nature of the singularity at r = rs remained unclear. In 1924 Arthur Eddington produced the first coordinate transformation (Eddington–Finkelstein coordinates) that showed that the singularity at r = rs was a coordinate artifact, although he seems to have been unaware of the significance of this discovery. Later, in 1932, Georges Lemaître
gave a different coordinate transformation (Lemaître coordinates) to the same effect and was the first to recognize that this implied that the singularity at r = rs was not physical. In 1939 Howard Robertson
showed that a free falling observer descending in the Scwharzschild metric would cross the r = rs singularity in a finite amount of proper time
even though this would take an infinite amount of time in terms of coordinate time t.
In 1950, John Synge
produced a paper that showed the maximal analytic extension
of the Schwarzschild metric, again showing that the singularity at r = rs was a coordinate artifact. This result was later rediscovered by Martin Kruskal
, who improved on Synge's result by providing a single set of coordinates that covered (almost) the entire spacetime. However due to the obscurity of the journals in which the papers of Lemaître and Synge were published their conclusions went unnoticed, with many of the major players in the field including Einstein believing that singularity at the Schwarzschild radius was physical.
Progress was only made in the 1960s when the more exact tools of differential geometry entered the field of general relativity allowing more exact definitions of what it means for a Lorentzian manifold to be singular. This lead to definitive identification of the r = rs singularity in the Schwarzschild metric as an event horizon
(a hypersurface in spacetime that can only be crossed in one direction).
, the Schwarzschild metric has the form: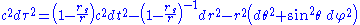
where:
The analogue of this solution in classical Newtonian theory of gravity corresponds to the gravitational field around a point particle.
In practice, the ratio rs/r is almost always extremely small. For example, the Schwarzschild radius rs of the Earth
is roughly 8.9 millimetre (0.350393700787402 in), while the sun, which is 3.3×105 times as massive has a Schwarzschild radius of approximately 3 km (1.9 mi).
A satellite
in a geosynchronous orbit
has a radius r that is roughly four billion times larger than the earth's Schwarzschild radius at 42164 km (26,199.6 mi). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black hole
s and other ultra-dense objects such as neutron star
s.
The Schwarzschild metric is a solution of Einstein's field equations in empty space, meaning that it is valid only outside the gravitating body. That is, for a spherical body of radius R the solution is valid for r > R. To describe the gravitational field both inside and outside the gravitating body the Schwarzschild solution must be matched with some suitable interior solution at r = R.
When considering an object falling into a black hole, it is better to use a different coordinate system such as Kruskal–Szekeres coordinates.
at r = 0 and r = rs; some of the metric components blow up at these radii. Since the Schwarzschild metric is only expected to be valid for radii larger than the radius R of the gravitating body, there is no problem as long as R > rs. For ordinary stars and planets this is always the case. For example, the radius of the Sun
is approximately 700,000 km, while its Schwarzschild radius is only 3 km.
The singularity at r = rs divides the Schwarzschild coordinates in two disconnected
patches. The outer patch with r > rs is the one that is related to the gravitational fields of stars and planets. The inner patch 0 < r < rs, which contains the singularity at r = 0, is completely separated from the outer patch by the singularity at r = rs. The Schwarzschild coordinates therefore give no physical connection between the two patches, which may be viewed as separate solutions. The singularity at r = rs is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions
. When changing to a different coordinate system (for example Lemaitre coordinates, Eddington-Finkelstein coordinates
, Kruskal-Szekeres coordinates
, Novikov coordinates, or Gullstrand–Painlevé coordinates) the metric becomes regular at r = rs and can extended the external patch to values of r smaller than rs. Using a different coordinate transformation one can then relate the extended external patch to the inner patch.
The case r = 0 is different, however. If one asks that the solution be valid for all r one runs into a true physical singularity, or gravitational singularity
, at the origin. To see that this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant, which is given by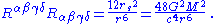
At r = 0 the curvature blows up (becomes infinite) indicating the presence of a singularity. At this point the metric, and space-time itself, is no longer well-defined. For a long time it was thought that such a solution was non-physical. However, a greater understanding of general relativity led to the realization that such singularities were a generic feature of the theory and not just an exotic special case. Such solutions are now believed to exist and are termed black hole
s.
The Schwarzschild solution, taken to be valid for all r > 0, is called a Schwarzschild black hole. It is a perfectly valid solution of the Einstein field equations, although it has some rather bizarre properties. For r < rs the Schwarzschild radial coordinate r becomes timelike and the time coordinate t becomes spacelike. A curve at constant r is no longer a possible worldline of a particle or observer, not even if a force is exerted to try to keep it there; this occurs because spacetime has been curved so much that the direction of cause and effect (the particle's future light cone
) points into the singularity. The surface r = rs demarcates what is called the event horizon
of the black hole. It represents the point past which light can no longer escape the gravitational field. Any physical object whose radius R becomes less than or equal to the Schwarzschild radius will undergo gravitational collapse
and become a black hole.
). Eddington gave alternative formulations of the Schwarzschild metric in terms of isotropic coordinates
(provided r ≥ 2GM/c2 ).
In isotropic spherical coordinates, one uses a different radial coordinate, r1, instead of r. They are related by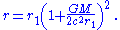
Using r1, the metric is
For isotropic rectangular coordinates x, y, z, where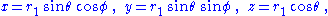
and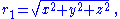
the metric then becomes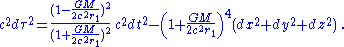
In the terms of these coordinates, the velocity of light at any point is the same in all directions, but it varies with radial distance r1 (from the point mass at the origin of coordinates), where it has the value
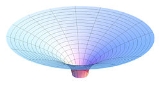
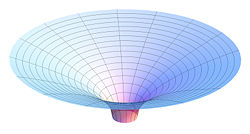 The spatial curvature of the Schwarzschild solution for
The spatial curvature of the Schwarzschild solution for  can be visualized as the graphic shows. Consider a constant time equatorial slice through the Schwarzschild solution (θ = π/2, t = constant) and let the position of a particle moving in this plane be described with the remaining Schwarzschild coordinates (r, φ). Imagine now that there is an additional Euclidean dimension w, which has no physical reality (it is not part of spacetime). Then replace the (r, φ) plane with a surface dimpled in the w direction according to the equation (Flamm's paraboloid)
can be visualized as the graphic shows. Consider a constant time equatorial slice through the Schwarzschild solution (θ = π/2, t = constant) and let the position of a particle moving in this plane be described with the remaining Schwarzschild coordinates (r, φ). Imagine now that there is an additional Euclidean dimension w, which has no physical reality (it is not part of spacetime). Then replace the (r, φ) plane with a surface dimpled in the w direction according to the equation (Flamm's paraboloid)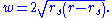
This surface has the property that distances measured within it match distances in the Schwarzschild metric, because with the definition of w above,
Thus, Flamm's paraboloid is useful for visualizing the spatial curvature of the Schwarzschild metric. It should not, however, be confused with a gravity well
. No ordinary (massive or massless) particle can have a worldline lying on the paraboloid, since all distances on it are spacelike (this is a cross-section at one moment of time, so all particles moving across it must have infinite velocity
). Even a tachyon
would not move along the path that one might naively expect from a "rubber sheet" analogy: in particular, if the dimple is drawn pointing upward rather than downward, the tachyon's path still curves toward the central mass, not away. See the gravity well
article for more information.
Flamm's paraboloid may be derived as follows. The Euclidean metric in the cylindrical coordinates (r, φ, w) is written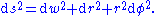
Letting the surface be described by the function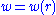 , the Euclidean metric can be written as
, the Euclidean metric can be written as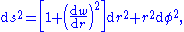
Comparing this with the Schwarzschild metric in the equatorial plane (θ = π/2) at a fixed time (t = constant, dt = 0)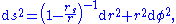
yields an integral expression for w(r):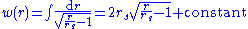
whose solution is Flamm's paraboloid.
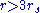 . Circular orbits with
. Circular orbits with  between
between  and
and 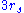 are unstable, and no circular orbits exist for
are unstable, and no circular orbits exist for  . The circular orbit of minimum radius
. The circular orbit of minimum radius  corresponds to an orbital velocity approaching the speed of light. It is possible for a particle to have a constant value of
corresponds to an orbital velocity approaching the speed of light. It is possible for a particle to have a constant value of  between
between 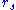 and
and 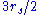 , but only if some force acts to keep it there.
, but only if some force acts to keep it there.
Noncircular orbits, such as Mercury's, dwell longer at small radii than would be expected classically. This can be seen as a less extreme version of the more dramatic case in which a particle passes through the event horizon and dwells inside it forever. Intermediate between the case of Mercury and the case of an object falling past the event horizon, there are exotic possibilities such as "knife-edge" orbits, in which the satellite can be made to execute an arbitrarily large number of nearly circular orbits, after which it flies back outward.
which takes the time axis (trajectory of the star) to itself. It omits the spatial translations (three dimensions) and boosts (three dimensions). It retains the time translations (one dimension) and rotations (three dimensions). Thus it has four dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time reversed and spatially inverted.
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Schwarzschild solution (or the Schwarzschild vacuum) describes the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
outside a spherical, uncharged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, non-rotating mass such as a (non-rotating) star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
, planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
, or black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
or Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
. The cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
is assumed to equal zero.
According to Birkhoff's theorem
Birkhoff's theorem (relativity)
In general relativity, Birkhoff's theorem states that any spherically symmetric solution of the vacuum field equations must be static and asymptotically flat. This means that the exterior solution must be given by the Schwarzschild metric....
, the Schwarzschild solution is the most general spherically symmetric
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
, vacuum solution
Vacuum solution (general relativity)
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress-energy tensor also vanishes identically, so that no matter or non-gravitational fields are present.More generally, a...
of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
. A Schwarzschild black hole or static black hole is a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
that has no charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
or angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. A Schwarzschild black hole has a Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.
The Schwarzschild black hole is characterized by a surrounding spherical surface, called the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
, which is situated at the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
, often called the radius of a black hole. Any non-rotating and non-charged mass that is smaller than its Schwarzschild radius forms a black hole. The solution of the Einstein field equations is valid for any mass M, so in principle (according to general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
theory) a Schwarzschild black hole of any mass could exist if conditions became sufficiently favorable to allow for its formation.
History
The Schwarzschild solution is named in honor of Karl SchwarzschildKarl Schwarzschild
Karl Schwarzschild was a German physicist. He is also the father of astrophysicist Martin Schwarzschild.He is best known for providing the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-rotating mass, which he accomplished...
, who found the exact solution in 1915, only about a month after the publication of Einstein's theory of general relativity. It was the first exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equations other than the trivial flat space solution. Schwarzschild had little time to think about his solution. He died shortly after his paper was published, as a result of a disease he contracted while serving in the German army during World War I
World War I
World War I , which was predominantly called the World War or the Great War from its occurrence until 1939, and the First World War or World War I thereafter, was a major war centred in Europe that began on 28 July 1914 and lasted until 11 November 1918...
.
Johannes Droste in 1915
independently produced the same solution as Schwarzschild, using a simpler more direct derivation.
In the early years of general relativity there was a lot of confusion about the nature of the singularities found in the Schwarzschild and other solutions of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
. In his 1916 paper Schwarzschild took the position that the singularity at r = rs should be identified with the coordinate singularity at the origin present in spherical coordinates on flat space. A more complete analysis of the singularity structure was given by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in the following year, identifying the singularities both at r = 0 and r = rs. Although there was general consent that the singularity at r = 0 was 'genuine' physical singularity, the nature of the singularity at r = rs remained unclear. In 1924 Arthur Eddington produced the first coordinate transformation (Eddington–Finkelstein coordinates) that showed that the singularity at r = rs was a coordinate artifact, although he seems to have been unaware of the significance of this discovery. Later, in 1932, Georges Lemaître
Georges Lemaître
Monsignor Georges Henri Joseph Édouard Lemaître was a Belgian priest, astronomer and professor of physics at the Catholic University of Louvain. He was the first person to propose the theory of the expansion of the Universe, widely misattributed to Edwin Hubble...
gave a different coordinate transformation (Lemaître coordinates) to the same effect and was the first to recognize that this implied that the singularity at r = rs was not physical. In 1939 Howard Robertson
Howard Robertson
Howard Robertson my refer to:*Howard Percy Robertson , American mathematician*Howard W. Robertson , American poet*Howard Robertson , architect of the Shell Centre...
showed that a free falling observer descending in the Scwharzschild metric would cross the r = rs singularity in a finite amount of proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
even though this would take an infinite amount of time in terms of coordinate time t.
In 1950, John Synge
John Synge
John Synge may refer to:* John Lighton Synge , Irish mathematician and physicist* John Millington Synge , Irish dramatist, poet, prose writer, and collector of folklore...
produced a paper that showed the maximal analytic extension
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the Schwarzschild metric, again showing that the singularity at r = rs was a coordinate artifact. This result was later rediscovered by Martin Kruskal
Martin Kruskal
Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis...
, who improved on Synge's result by providing a single set of coordinates that covered (almost) the entire spacetime. However due to the obscurity of the journals in which the papers of Lemaître and Synge were published their conclusions went unnoticed, with many of the major players in the field including Einstein believing that singularity at the Schwarzschild radius was physical.
Progress was only made in the 1960s when the more exact tools of differential geometry entered the field of general relativity allowing more exact definitions of what it means for a Lorentzian manifold to be singular. This lead to definitive identification of the r = rs singularity in the Schwarzschild metric as an event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
(a hypersurface in spacetime that can only be crossed in one direction).
The Schwarzschild metric
In Schwarzschild coordinatesSchwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
, the Schwarzschild metric has the form:
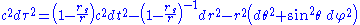
where:
- τ is the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
(time measured by a clock moving with the particle) in seconds, - c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in meters per second, - t is the time coordinate (measured by a stationary clock at infinity) in seconds,
- r is the radial coordinate (circumference of a circle centered on the star divided by 2π) in meters,
- θ is the colatitudeColatitudeIn spherical coordinates, colatitude is the complementary angle of the latitude, i.e. the difference between 90° and the latitude.-Astronomical use:The colatitude is useful in astronomy because it refers to the zenith distance of the celestial poles...
(angle from North) in radians, - φ is the longitudeLongitudeLongitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
in radians, and - rs is the Schwarzschild radiusSchwarzschild radiusThe Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
(in meters) of the massive body, which is related to its mass M by rs = 2GM/c2, where G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
.
The analogue of this solution in classical Newtonian theory of gravity corresponds to the gravitational field around a point particle.
In practice, the ratio rs/r is almost always extremely small. For example, the Schwarzschild radius rs of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is roughly 8.9 millimetre (0.350393700787402 in), while the sun, which is 3.3×105 times as massive has a Schwarzschild radius of approximately 3 km (1.9 mi).
A satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
in a geosynchronous orbit
Geosynchronous orbit
A geosynchronous orbit is an orbit around the Earth with an orbital period that matches the Earth's sidereal rotation period...
has a radius r that is roughly four billion times larger than the earth's Schwarzschild radius at 42164 km (26,199.6 mi). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s and other ultra-dense objects such as neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s.
The Schwarzschild metric is a solution of Einstein's field equations in empty space, meaning that it is valid only outside the gravitating body. That is, for a spherical body of radius R the solution is valid for r > R. To describe the gravitational field both inside and outside the gravitating body the Schwarzschild solution must be matched with some suitable interior solution at r = R.
When considering an object falling into a black hole, it is better to use a different coordinate system such as Kruskal–Szekeres coordinates.
Singularities and black holes
The Schwarzschild solution appears to have singularitiesMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
at r = 0 and r = rs; some of the metric components blow up at these radii. Since the Schwarzschild metric is only expected to be valid for radii larger than the radius R of the gravitating body, there is no problem as long as R > rs. For ordinary stars and planets this is always the case. For example, the radius of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
is approximately 700,000 km, while its Schwarzschild radius is only 3 km.
The singularity at r = rs divides the Schwarzschild coordinates in two disconnected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
patches. The outer patch with r > rs is the one that is related to the gravitational fields of stars and planets. The inner patch 0 < r < rs, which contains the singularity at r = 0, is completely separated from the outer patch by the singularity at r = rs. The Schwarzschild coordinates therefore give no physical connection between the two patches, which may be viewed as separate solutions. The singularity at r = rs is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions
Coordinate conditions
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the real world does not care about our coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions...
. When changing to a different coordinate system (for example Lemaitre coordinates, Eddington-Finkelstein coordinates
Eddington-Finkelstein coordinates
In general relativity Eddington–Finkelstein coordinates, named for Arthur Stanley Eddington and David Finkelstein, are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics...
, Kruskal-Szekeres coordinates
Kruskal-Szekeres coordinates
In general relativity Kruskal–Szekeres coordinates, named for Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole...
, Novikov coordinates, or Gullstrand–Painlevé coordinates) the metric becomes regular at r = rs and can extended the external patch to values of r smaller than rs. Using a different coordinate transformation one can then relate the extended external patch to the inner patch.
The case r = 0 is different, however. If one asks that the solution be valid for all r one runs into a true physical singularity, or gravitational singularity
Gravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
, at the origin. To see that this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant, which is given by
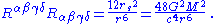
At r = 0 the curvature blows up (becomes infinite) indicating the presence of a singularity. At this point the metric, and space-time itself, is no longer well-defined. For a long time it was thought that such a solution was non-physical. However, a greater understanding of general relativity led to the realization that such singularities were a generic feature of the theory and not just an exotic special case. Such solutions are now believed to exist and are termed black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s.
The Schwarzschild solution, taken to be valid for all r > 0, is called a Schwarzschild black hole. It is a perfectly valid solution of the Einstein field equations, although it has some rather bizarre properties. For r < rs the Schwarzschild radial coordinate r becomes timelike and the time coordinate t becomes spacelike. A curve at constant r is no longer a possible worldline of a particle or observer, not even if a force is exerted to try to keep it there; this occurs because spacetime has been curved so much that the direction of cause and effect (the particle's future light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
) points into the singularity. The surface r = rs demarcates what is called the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of the black hole. It represents the point past which light can no longer escape the gravitational field. Any physical object whose radius R becomes less than or equal to the Schwarzschild radius will undergo gravitational collapse
Gravitational collapse
Gravitational collapse is the inward fall of a body due to the influence of its own gravity. In any stable body, this gravitational force is counterbalanced by the internal pressure of the body, in the opposite direction to the force of gravity...
and become a black hole.
Alternative (isotropic) formulations of the Schwarzschild metric
The original form of the Schwarzschild metric involves anisotropic coordinates, in terms of which the velocity of light is not the same for the radial and transverse directions (pointed out by A S EddingtonArthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
). Eddington gave alternative formulations of the Schwarzschild metric in terms of isotropic coordinates
Isotropic coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. There are several different types of coordinate chart which are adapted to this family of nested spheres; the best known is the Schwarzschild chart, but the isotropic chart is also often...
(provided r ≥ 2GM/c2 ).
In isotropic spherical coordinates, one uses a different radial coordinate, r1, instead of r. They are related by
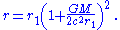
Using r1, the metric is

For isotropic rectangular coordinates x, y, z, where
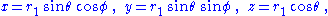
and
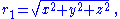
the metric then becomes
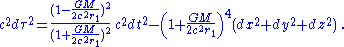
In the terms of these coordinates, the velocity of light at any point is the same in all directions, but it varies with radial distance r1 (from the point mass at the origin of coordinates), where it has the value

Flamm's paraboloid

 can be visualized as the graphic shows. Consider a constant time equatorial slice through the Schwarzschild solution (θ = π/2, t = constant) and let the position of a particle moving in this plane be described with the remaining Schwarzschild coordinates (r, φ). Imagine now that there is an additional Euclidean dimension w, which has no physical reality (it is not part of spacetime). Then replace the (r, φ) plane with a surface dimpled in the w direction according to the equation (Flamm's paraboloid)
can be visualized as the graphic shows. Consider a constant time equatorial slice through the Schwarzschild solution (θ = π/2, t = constant) and let the position of a particle moving in this plane be described with the remaining Schwarzschild coordinates (r, φ). Imagine now that there is an additional Euclidean dimension w, which has no physical reality (it is not part of spacetime). Then replace the (r, φ) plane with a surface dimpled in the w direction according to the equation (Flamm's paraboloid)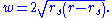
This surface has the property that distances measured within it match distances in the Schwarzschild metric, because with the definition of w above,

Thus, Flamm's paraboloid is useful for visualizing the spatial curvature of the Schwarzschild metric. It should not, however, be confused with a gravity well
Gravity well
A gravity well or gravitational well is a conceptual model of the gravitational field surrounding a body in space. The more massive the body the deeper and more extensive the gravity well associated with it. The Sun has a far-reaching and deep gravity well. Asteroids and small moons have much...
. No ordinary (massive or massless) particle can have a worldline lying on the paraboloid, since all distances on it are spacelike (this is a cross-section at one moment of time, so all particles moving across it must have infinite velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
). Even a tachyon
Tachyon
A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
would not move along the path that one might naively expect from a "rubber sheet" analogy: in particular, if the dimple is drawn pointing upward rather than downward, the tachyon's path still curves toward the central mass, not away. See the gravity well
Gravity well
A gravity well or gravitational well is a conceptual model of the gravitational field surrounding a body in space. The more massive the body the deeper and more extensive the gravity well associated with it. The Sun has a far-reaching and deep gravity well. Asteroids and small moons have much...
article for more information.
Flamm's paraboloid may be derived as follows. The Euclidean metric in the cylindrical coordinates (r, φ, w) is written
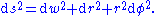
Letting the surface be described by the function
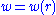 , the Euclidean metric can be written as
, the Euclidean metric can be written as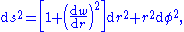
Comparing this with the Schwarzschild metric in the equatorial plane (θ = π/2) at a fixed time (t = constant, dt = 0)
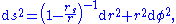
yields an integral expression for w(r):
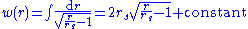
whose solution is Flamm's paraboloid.
Orbital motion
A particle orbiting in the Schwarzschild metric can have a stable circular orbit with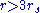 . Circular orbits with
. Circular orbits with  between
between 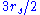 and
and 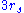 are unstable, and no circular orbits exist for
are unstable, and no circular orbits exist for  . The circular orbit of minimum radius
. The circular orbit of minimum radius  corresponds to an orbital velocity approaching the speed of light. It is possible for a particle to have a constant value of
corresponds to an orbital velocity approaching the speed of light. It is possible for a particle to have a constant value of  between
between 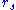 and
and 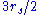 , but only if some force acts to keep it there.
, but only if some force acts to keep it there.Noncircular orbits, such as Mercury's, dwell longer at small radii than would be expected classically. This can be seen as a less extreme version of the more dramatic case in which a particle passes through the event horizon and dwells inside it forever. Intermediate between the case of Mercury and the case of an object falling past the event horizon, there are exotic possibilities such as "knife-edge" orbits, in which the satellite can be made to execute an arbitrarily large number of nearly circular orbits, after which it flies back outward.
Symmetries
The group of isometries of the Schwarzschild metric is the subgroup of the ten-dimensional Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
which takes the time axis (trajectory of the star) to itself. It omits the spatial translations (three dimensions) and boosts (three dimensions). It retains the time translations (one dimension) and rotations (three dimensions). Thus it has four dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time reversed and spatially inverted.
Quotes
"" (It is always pleasant to have exact solutions in simple form at your disposal.) – Karl Schwarzschild, 1916.
See also
- Deriving the Schwarzschild solutionDeriving the Schwarzschild solutionThe Schwarzschild solution is one of the simplest and most useful solutions of theEinstein field equations . It describes spacetime in the vicinity of a non-rotating massive spherically-symmetric object...
- Reissner–Nordström metric (charged, non-rotating solution)
- Kerr metricKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
(uncharged, rotating solution) - Kerr–Newman metric (charged, rotating solution)
- BKL singularityBKL singularityA BKL singularity is a model of the dynamic evolution of the Universe near the initial singularity, described by an anisotropic, homogeneous, chaotic solution to Einstein's field equations of gravitation...
(interior solution) - Black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, a general review - Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
- Kruskal–Szekeres coordinates
- Eddington–Finkelstein coordinates
- Gullstrand–Painlevé coordinates
- Lemaitre coordinates (Schwarzschild solution in synchronous coordinates)
- Frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
(Lemaître observers in the Schwarzschild vacuum)

