
Equation solving
Encyclopedia
In mathematics
, to solve an equation is to find what values (number
s, functions
, sets, etc.) fulfill a condition stated in the form of an equation
(two expression
s related by equality). These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled. To be precise, what is sought are often not necessarily actual values, but, more in general, mathematical expressions. A solution of the equation is an assignment of expressions to the unknowns that satisfies the equation; in other words, expressions such that, when they are substituted
for the unknowns, the equation becomes a tautology
(a provably
true statement).
For example, the equation is solved for the unknown x by the solution , since substituting for x in the equation results in , a true statement. It is also possible to take the variable y to be the unknown, and then the equation is solved by . Or x and y can both be treated as unknowns, and then there are many solutions to the equation, some of which are – that is, and – and , and, in general, for all possible values of a.
Depending on the problem, the task may be to find one solution – any solution will do – or all solutions. The set of all solutions is called the solution set. It is also possible that the task is to find a solution, among possibly many, that is best in some respect. Problems of that nature are called optimization problem
s; solving an optimization problem is generally not referred to as "equation solving".
A wording such as "an equation in x and y", or "solve for x and y", implies that the unknowns are as indicated: in these cases x and y.
where c is a constant, whose solutions are the members of the inverse image
where T1×···×Tn is the domain of the function. Note that the set of solutions can be empty (there are no solutions), a singleton (there is exactly one solution), finite, or infinite (there are infinitely many solutions).
For example, an equation such as
with unknowns x, y and z, can be solved by first modifying the equation in some way while keeping it equivalent, such as subtracting 21z from both sides of the equation to obtain
In this particular case there is not just one solution to this equation, but an infinite set of solutions, which can be written
One particular solution is x = 0, y = 0, z = 0. Two other solutions are x = 3, y = 6, z = 1, and x = 8, y = 9, z = 2. In fact, this particular set of solutions describes a plane in three-dimensional space, which passes through the three points with these coordinates.
in which c is a given constant, becomes true.
For example, let us examine a classic one-variable case. Using the squaring function on the integers, that is, the function ƒ whose domain are the integer
s (the whole numbers) defined by:
consider the equation
Its solution set is {}, the empty set, since 2 is not the square of an integer, so no integer solves this equation. However note that in attempting to find solutions for this equation, if we modify the function's definition – more specifically, the function's domain, we can find solutions to this equation. So, if we were instead to define that the domain of ƒ consists of the real number
s, the equation above has two solutions, and its solution set is
We have already seen that certain solutions sets can describe surfaces. For example, in studying elementary mathematics, one knows that the solution set of an equation in the form ax + by = c with a, b, and c real-valued constants, with a and b not both equal to zero, forms a line
in the vector space
R2. However, it may not always be easy to graphically depict solutions sets – for example, the solution set to an equation in the form ax + by + cz + dw = k (with a, b, c, d, and k real-valued constants) is a hyperplane
.
In general, given a class of equations, there may be no systematic method (algorithm
) that is guaranteed to work. This may be due to a lack of mathematical knowledge; some problems were only solved after centuries of effort. But this also reflects that, in general, no such method can exist: some problems are known to be unsolvable by an algorithm, such as Hilbert's tenth problem
, which was proved unsolvable in 1970.
For several classes of equations algorithms have been found for solving them, some of which have been implemented and incorporated in computer algebra system
s, but often require no more sophisticated technology than pencil and paper. In some other cases, heuristic
methods are known that are often successful but that are not guaranteed to lead to success.
, for example), or can be limited to a finite number of possibilities (as is the case with some Diophantine equation
s), the solution set can be found by brute force
, that is, by testing each of the possible values. It may be the case, though, that the number of possibilities to be considered, although finite, is so huge that an exhaustive search is not practically feasible; this is, in fact, a requirement for strong encryption
methods.
As with all kinds of problem solving
, trial and error
may sometimes yield a solution, in particular where the form of the equation, or its similarity to another equation with a known solution, may lead to an "inspired guess" at the solution. If a guess, when tested, fails to be a solution, consideration of the way in which it fails may lead to a modified guess.
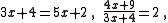
can be solved using the methods of elementary algebra
.
.
equations of degree up to four can be solved exactly using algebraic methods, of which the quadratic formula is the simplest example. Polynomial equations with a degree of five or higher require in general numerical methods (see below) or special functions such as Bring radical
s, although some specific cases may be solvable algebraically, for example
(by using the Rational root theorem), and
(by using the substitution x = z1/3, which simplifies this to a quadratic equation
in z).
s. In some case a brute force approach can be used, as mentioned above. In some other cases, in particular if the equation is in one unknown, it is possible to solve the equation for rational
-valued unknowns (see Rational root theorem), and then find solutions to the Diophantine equation by restricting the solution set to integer-valued solutions. For example, the polynomial equation
has as rational solutions x = −1/2 and x = 3, and so, viewed as a Diophantine equation, it has the unique solution x = 3.
In general, however, Diophantine equations belong to the hardest equations to solve.
by considering what is known as the inverse function
of h.
Given a function h : A → B, the inverse function, denoted h−1, defined as h−1 : B → A is a function such that
Now, if we apply the inverse function to both sides of
we obtain
and we have found the solution to the equation. However, depending on the function, the inverse may be difficult to be defined, or may not be a function on all of the set B (only on some subset), and have many values at some point.
If just one solution will do, instead of the full solution set, it is actually sufficient if only the functional identity
holds. For example, the projection
defined by has no post-inverse, but it has a pre-inverse π1−1 defined by . Indeed, the equation
is solved by = π1−1(c) = (c, 0).
Examples of inverse functions include the nth root
(inverse of xn); the logarithm
(inverse of ax); the inverse trigonometric function
s; and Lambert's W function (inverse of xex).
as P = QR, the solution set of the original solution consists of the union of the solution sets of the two equations Q = 0 and R = 0.
For example, the equation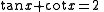
can be rewritten as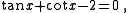
which can be factored, using the identity (provided that the components are defined), as
The two equations and have identical solution sets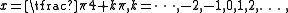
which therefore is the solution set of the original equation.
s, simple methods to solve equations can fail. Often, root-finding algorithm
s like the Newton–Raphson method can be used to find a numerical solution to an equation, which, for some applications, can be entirely sufficient to solve some problem.
.
and vectors
of real number
s can often be solved by using methods from linear algebra
.
s, both numerically and analytically
. A particular class of problem that can be considered to belong here is integration
, and a method for finding analytical solutions for the indefinite case is the Risch algorithm
– unfortunately too complicated for use with pencil and paper.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, to solve an equation is to find what values (number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s, functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, sets, etc.) fulfill a condition stated in the form of an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
(two expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
s related by equality). These expressions contain one or more unknowns, which are free variables for which values are sought that cause the condition to be fulfilled. To be precise, what is sought are often not necessarily actual values, but, more in general, mathematical expressions. A solution of the equation is an assignment of expressions to the unknowns that satisfies the equation; in other words, expressions such that, when they are substituted
Substitution (logic)
Substitution is a fundamental concept in logic. Substitution is a syntactic transformation on strings of symbols of a formal language.In propositional logic, a substitution instance of a propositional formula is a second formula obtained by replacing symbols of the original formula by other formulas...
for the unknowns, the equation becomes a tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
(a provably
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
true statement).
For example, the equation is solved for the unknown x by the solution , since substituting for x in the equation results in , a true statement. It is also possible to take the variable y to be the unknown, and then the equation is solved by . Or x and y can both be treated as unknowns, and then there are many solutions to the equation, some of which are – that is, and – and , and, in general, for all possible values of a.
Depending on the problem, the task may be to find one solution – any solution will do – or all solutions. The set of all solutions is called the solution set. It is also possible that the task is to find a solution, among possibly many, that is best in some respect. Problems of that nature are called optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s; solving an optimization problem is generally not referred to as "equation solving".
A wording such as "an equation in x and y", or "solve for x and y", implies that the unknowns are as indicated: in these cases x and y.
Overview
In one general case, we have a situation such as- ƒ (x1,...,xn) = c,
where c is a constant, whose solutions are the members of the inverse image
- ƒ −1[c] = {(a1,...,an) ∈ T1×···×Tn | ƒ (a1,...,an) = c},
where T1×···×Tn is the domain of the function. Note that the set of solutions can be empty (there are no solutions), a singleton (there is exactly one solution), finite, or infinite (there are infinitely many solutions).
For example, an equation such as
- 3x + 2y = 21z
with unknowns x, y and z, can be solved by first modifying the equation in some way while keeping it equivalent, such as subtracting 21z from both sides of the equation to obtain
- 3x + 2y − 21z = 0
In this particular case there is not just one solution to this equation, but an infinite set of solutions, which can be written
- {(x, y, z) | 3x + 2y − 21z = 0}.
One particular solution is x = 0, y = 0, z = 0. Two other solutions are x = 3, y = 6, z = 1, and x = 8, y = 9, z = 2. In fact, this particular set of solutions describes a plane in three-dimensional space, which passes through the three points with these coordinates.
Solution sets
If the solution set is empty, then there are no xi such that the equation- ƒ (x1,...,xn) = c,
in which c is a given constant, becomes true.
For example, let us examine a classic one-variable case. Using the squaring function on the integers, that is, the function ƒ whose domain are the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s (the whole numbers) defined by:
- ƒ (x) = x2,
consider the equation
- ƒ (x) = 2.
Its solution set is {}, the empty set, since 2 is not the square of an integer, so no integer solves this equation. However note that in attempting to find solutions for this equation, if we modify the function's definition – more specifically, the function's domain, we can find solutions to this equation. So, if we were instead to define that the domain of ƒ consists of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the equation above has two solutions, and its solution set is
- {√2, −√2}.
We have already seen that certain solutions sets can describe surfaces. For example, in studying elementary mathematics, one knows that the solution set of an equation in the form ax + by = c with a, b, and c real-valued constants, with a and b not both equal to zero, forms a line
Line
- Science and technology :* Line , a circuit or loop.** A power line for electric power transmission** line power or lines power, domestic mains electricity.** telephone line** RF transmission line...
in the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
R2. However, it may not always be easy to graphically depict solutions sets – for example, the solution set to an equation in the form ax + by + cz + dw = k (with a, b, c, d, and k real-valued constants) is a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
.
Methods of solution
The methods for solving equations generally depend on the type of equation, both the kind of expressions in the equation and the kind of values that may be assumed by the unknowns. The variety in types of equations is large, and so are the corresponding methods. Only a few specific types are mentioned below; a comprehensive treatment is not possible.In general, given a class of equations, there may be no systematic method (algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
) that is guaranteed to work. This may be due to a lack of mathematical knowledge; some problems were only solved after centuries of effort. But this also reflects that, in general, no such method can exist: some problems are known to be unsolvable by an algorithm, such as Hilbert's tenth problem
Hilbert's tenth problem
Hilbert's tenth problem is the tenth on the list of Hilbert's problems of 1900. Its statement is as follows:Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite...
, which was proved unsolvable in 1970.
For several classes of equations algorithms have been found for solving them, some of which have been implemented and incorporated in computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s, but often require no more sophisticated technology than pencil and paper. In some other cases, heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
methods are known that are often successful but that are not guaranteed to lead to success.
Brute force, trial and error, inspired guess
If the solution set of an equation is restricted to a finite set (as is the case for equations in modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, for example), or can be limited to a finite number of possibilities (as is the case with some Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s), the solution set can be found by brute force
Brute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
, that is, by testing each of the possible values. It may be the case, though, that the number of possibilities to be considered, although finite, is so huge that an exhaustive search is not practically feasible; this is, in fact, a requirement for strong encryption
Encryption
In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
methods.
As with all kinds of problem solving
Problem solving
Problem solving is a mental process and is part of the larger problem process that includes problem finding and problem shaping. Consideredthe most complex of all intellectual functions, problem solving has been defined as higher-order cognitive process that requires the modulation and control of...
, trial and error
Trial and error
Trial and error, or trial by error, is a general method of problem solving, fixing things, or for obtaining knowledge."Learning doesn't happen from failure itself but rather from analyzing the failure, making a change, and then trying again."...
may sometimes yield a solution, in particular where the form of the equation, or its similarity to another equation with a known solution, may lead to an "inspired guess" at the solution. If a guess, when tested, fails to be a solution, consideration of the way in which it fails may lead to a modified guess.
Elementary algebra
Equations involving linear or simple rational functions of a single real-valued unknown, say x, such as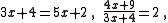
can be solved using the methods of elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
.
Systems of linear equations
Smaller systems of linear equations can be solved likewise by methods of elementary algebra. For solving large systems numerically, algorithms are used that are based on linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Polynomial equations
PolynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equations of degree up to four can be solved exactly using algebraic methods, of which the quadratic formula is the simplest example. Polynomial equations with a degree of five or higher require in general numerical methods (see below) or special functions such as Bring radical
Bring radical
In algebra, a Bring radical or ultraradical of a complex number a is a root of the polynomialx^5+x+a. \,In algebra, a Bring radical or ultraradical of a complex number a is a root of the polynomialx^5+x+a. \,In algebra, a Bring radical or ultraradical of a complex number a is a root...
s, although some specific cases may be solvable algebraically, for example
- 4x5 − x3 − 3 = 0
(by using the Rational root theorem), and
- x6 − 5x3 + 6 = 0,
(by using the substitution x = z1/3, which simplifies this to a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
in z).
Diophantine equations
In Diophantine equations the solutions are required to be integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. In some case a brute force approach can be used, as mentioned above. In some other cases, in particular if the equation is in one unknown, it is possible to solve the equation for rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
-valued unknowns (see Rational root theorem), and then find solutions to the Diophantine equation by restricting the solution set to integer-valued solutions. For example, the polynomial equation

has as rational solutions x = −1/2 and x = 3, and so, viewed as a Diophantine equation, it has the unique solution x = 3.
In general, however, Diophantine equations belong to the hardest equations to solve.
Inverse functions
In the simple case of a function of one variable, say, h(x), we can solve an equation of the form- h(x) = c, c constant
by considering what is known as the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of h.
Given a function h : A → B, the inverse function, denoted h−1, defined as h−1 : B → A is a function such that
- h−1(h(x)) = h(h−1(x)) = x.
Now, if we apply the inverse function to both sides of
- h(x) = c, where c is a constant value in B,
we obtain
- h−1(h(x)) = h−1(c)
- x = h−1(c)
and we have found the solution to the equation. However, depending on the function, the inverse may be difficult to be defined, or may not be a function on all of the set B (only on some subset), and have many values at some point.
If just one solution will do, instead of the full solution set, it is actually sufficient if only the functional identity
- h(h−1(x)) = x
holds. For example, the projection
Projection
Projection, projector, or projective may refer to:* The display of an image by devices such as:** Movie projector** Video projector** Overhead projector** Slide projector** Camera obscura** Projection screen...
defined by has no post-inverse, but it has a pre-inverse π1−1 defined by . Indeed, the equation
- π1(x, y) = c
is solved by = π1−1(c) = (c, 0).
Examples of inverse functions include the nth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
(inverse of xn); the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
(inverse of ax); the inverse trigonometric function
Inverse trigonometric function
In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
s; and Lambert's W function (inverse of xex).
Factorization
If the left-hand side expression P of an equation P = 0 can be factoredFactorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
as P = QR, the solution set of the original solution consists of the union of the solution sets of the two equations Q = 0 and R = 0.
For example, the equation
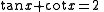
can be rewritten as
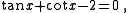
which can be factored, using the identity (provided that the components are defined), as

The two equations and have identical solution sets
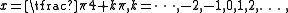
which therefore is the solution set of the original equation.
Numerical methods
With more complicated equations in real or complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, simple methods to solve equations can fail. Often, root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
s like the Newton–Raphson method can be used to find a numerical solution to an equation, which, for some applications, can be entirely sufficient to solve some problem.
Taylor series
One well-studied area of mathematics involves examining whether we can create some simple function to approximate a more complex equation near a given point. In fact, polynomials in one or several variables can be used to approximate functions in this way – these are known as Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
.
Matrix equations
Equations involving matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and vectors
Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can often be solved by using methods from linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Differential equations
There is a vast body of methods for solving various kinds of differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, both numerically and analytically
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. A particular class of problem that can be considered to belong here is integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, and a method for finding analytical solutions for the indefinite case is the Risch algorithm
Risch algorithm
The Risch algorithm, named after Robert Henry Risch, is an algorithm for the calculus operation of indefinite integration . The algorithm transforms the problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational...
– unfortunately too complicated for use with pencil and paper.
See also
- Simultaneous equationsSimultaneous equationsIn mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
- Equating coefficientsEquating coefficientsIn mathematics, the method of equating the coefficients is a way of solving a functional equation of two polynomials for a number of unknown parameters. It relies on the fact that two polynomials are identical precisely when all corresponding coefficients are equal...
- Solving the geodesic equationsSolving the geodesic equationsSolving the geodesic equations is a procedure used in mathematics, particularly Riemannian geometry, and in physics, particularly in general relativity, that results in obtaining geodesics. Physically, these represent the paths of particles with no proper acceleration, their motion satisfying the...

