Electronic band structure
Encyclopedia
In solid-state physics
, the electronic band structure (or simply band structure) of a solid
describes those ranges of energy
an electron
is "forbidden" or "allowed" to have. Band structure derives from the diffraction
of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system
and Bravais lattice. The band structure of a material determines several characteristics, in particular the material's electronic and optical properties.
s, which form a discrete set of energy
levels. If several atoms are brought together into a molecule, their atomic orbitals split, as in a coupled oscillation. This produces a number of molecular orbital
s proportional to the number of atoms. When a large number of atoms (of order or more) are brought together to form a solid, the number of orbitals becomes exceedingly large. Consequently, the difference in energy between them becomes very small. Thus, in solids the levels form continuous bands of energy rather than the discrete energy levels of the atoms in isolation. However, some intervals of energy contain no orbitals, no matter how many atoms are aggregated, forming band gaps.
Within an energy band, energy levels form a near continuum. First, the separation between energy levels in a solid is comparable with the energy that electrons constantly exchange with phonon
s (atom
ic vibrations
). Second, it is comparable with the energy uncertainty due to the Heisenberg uncertainty principle, for reasonably long intervals of time. As a result, the separation between energy levels is of no consequence.
Several approaches to finding band structure are discussed below.
 Any solid has a large number of bands. In theory, a solid can have infinitely many bands (just as an atom has infinitely many energy levels). However, all but a few of these bands lie at energies so high that any electron that attains those energies will escape from the solid. These bands are usually disregarded.
Any solid has a large number of bands. In theory, a solid can have infinitely many bands (just as an atom has infinitely many energy levels). However, all but a few of these bands lie at energies so high that any electron that attains those energies will escape from the solid. These bands are usually disregarded.
Bands have different widths, based upon the properties of the atomic orbitals from which they arise. Also, allowed bands may overlap, producing (for practical purposes) a single large band.
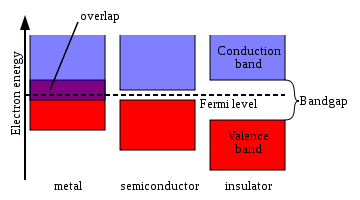
Figure 1 shows a simplified picture of the bands in a solid that allows the three major types of materials to be identified: metals, semiconductors and insulators.
Metal
s contain a band that is partly empty and partly filled regardless of temperature. Therefore they have very high conductivity.
The lowermost, almost fully occupied band in an insulator
or semiconductor
, is called the valence band
by analogy with the valence electron
s of individual atoms. The uppermost, almost unoccupied band is called the conduction band
because only when electrons are excited to the conduction band can current flow in these materials. The difference between insulators and semiconductors is only that the forbidden band gap
between the valence band and conduction band is larger in an insulator, so that fewer electrons are found there and the electrical conductivity is lower. Because one of the main mechanisms for electrons to be excited to the conduction band is due to thermal energy, the conductivity of semiconductors is strongly dependent on the temperature of the material.
This band gap is one of the most useful aspects of the band structure, as it strongly influences the electrical and optical properties of the material. Electrons can transfer from one band to the other by means of carrier generation and recombination
processes. The band gap and defect states created in the band gap by doping can be used to create semiconductor device
s such as solar cell
s, diode
s, transistor
s, laser diode
s, and others.
. The Schrödinger equation
is solved for the crystal, which has Bloch wave
s as solutions:
 ,
,
where k is called the wavevector, and is related to the direction of motion of the electron in the crystal, and n is the band index, which simply numbers the energy bands. The wavevector k takes on values within the Brillouin zone
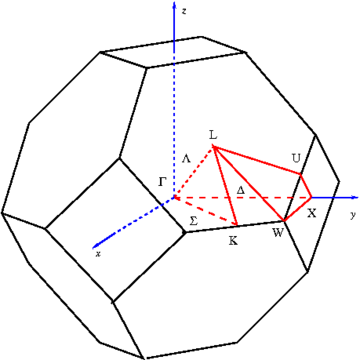
(BZ) corresponding to the crystal lattice, and particular directions/points in the BZ are assigned conventional names like Γ, Δ, Λ, Σ, etc. These directions are shown for the face-centered cubic lattice geometry in Figure 2.
The available energies for the electron also depend upon k, as shown in Figure 3 for silicon in the more complex energy band diagram at the right. In this diagram the topmost energy of the valence band is labeled Ev and the bottom energy in the conduction band is labeled Ec. Note that for silicon, the top of the valence band is not directly below the bottom of the conduction band (Ev is for an electron traveling in direction Γ, Ec in direction X), so silicon is called an indirect gap material. For an electron to be excited from the valence band to the conduction band within an indirect gap material, it needs something to give it both energy Ec – Ev and a change in direction/momentum. In other semiconductors (for example III-V materials, such as GaAs) both Ec and Ev are at Γ, and therefore these materials are direct gap materials (no momentum change required). Direct gap materials benefit the operation of semiconductor laser diodes.
Anderson's rule
is used to align band diagrams between two different semiconductors in contact.
line materials, quasi-crystalline and amorphous solid
s may also exhibit band structures. However, the periodic nature and symmetrical properties of crystalline materials makes it much easier to examine the band structures of these materials theoretically. In addition, the well-defined symmetry axes of crystalline materials makes it possible to determine the dispersion relation
ship between the momentum (a 3-dimension vector quantity) and energy of a material. As a result, virtually all of the existing theoretical work on the electronic band structure of solids has focused on crystalline materials.
in a band could be very large for some materials, it may not be uniform. It approaches zero at the band boundaries, and is generally highest near the middle of a band.
The density of states for the free electron model
in three dimensions is given by,
. The probability is given by the following expression:

where:
The Fermi level naturally is the level at which the electrons and protons are balanced.
At T=0, the distribution is a simple step function
:

At nonzero temperatures, the step "smooths out", so that an appreciable number of states below the Fermi level are empty, and some states above the Fermi level are filled.
is the special case of electron waves in a periodic crystal lattice using Bloch waves as treated generally in the dynamical theory of diffraction
. Every crystal is a periodic structure which can be characterized by a Bravais lattice, and for each Bravais lattice we can determine the reciprocal lattice
, which encapsulates the periodicity in a set of three reciprocal lattice vectors (b1,b2,b3). Now, any periodic potential V(r) which shares the same periodicity as the direct lattice can be expanded out as a Fourier series
whose only non-vanishing components are those associated with the reciprocal lattice vectors. So the expansion can be written as:

where K = m1b1 + m2b2 + m3b3 for any set of integers (m1,m2,m3).
From this theory, an attempt can be made to predict the band structure of a particular material, however most ab initio methods for electronic structure calculations fail to predict the observed band gap.
which states that electrons in a periodic potential have wavefunction
s and energies which are periodic in wavevector up to a constant phase shift between neighboring reciprocal lattice
vectors. The consequences of periodicity are described mathematically by the Bloch wavefunction:

where the function is periodic over the crystal lattice, that is,
is periodic over the crystal lattice, that is,
 .
.
Here index n refers to the n-th energy band, wavevector k is related to the direction of motion of the electron, r is position in the crystal, and R is location of an atomic site.
The NFE model works particularly well in materials like metal
s where distances between neighbouring atoms are small. In such materials
the overlap of atomic orbital
s and potentials on neighbouring atom
s is relatively large. In that case the wave function of the electron can be approximated by a (modified) plane wave. The band structure of a metal like Aluminum even gets close to the Empty Lattice Approximation
.
 is well approximated by a linear combination
is well approximated by a linear combination
of atomic orbitals .
.
 ,
,
where the coefficients are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by:
are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by:
 ;
;
in which is the periodic part of the Bloch wave and the integral is over the Brillouin zone
is the periodic part of the Bloch wave and the integral is over the Brillouin zone
. Here index n refers to the n-th energy band in the crystal. The Wannier functions are localized near atomic sites, like atomic orbitals, but being defined in terms of Bloch functions they are accurately related to solutions based upon the crystal potential. Wannier functions on different atomic sites R are orthogonal. The Wannier functions can be used to form the Schrödinger solution for the n-th energy band as:
 .
.
The TB model works well in materials with limited overlap between atomic orbital
s and potentials on neighbouring atoms. Band structures of materials like Si
, GaAs
, SiO2 and diamond
for instance are well described by TB-Hamiltonians on the basis of atomic sp3 orbitals. In transition metals a mixed TB-NFE model is used to describe the broad NFE conduction band
and the narrow embedded TB d-bands. The radial functions of
the atomic orbital part
of the Wannier functions are most easily calculated by the use of pseudopotential
methods. NFE, TB or combined NFE-TB band structure
calculations,
sometimes extended with wave function approximations based on pseudopotential methods, are often used as an economic starting point for further calculations.
is approximated as a constant. Continuity of the potential between the atom-centered spheres and interstitial region is enforced.
A variational implementation was suggested by Korringa and by Kohn
and Rostocker, and is often referred to as the KKR model
.
that tries to cope with the electron-electron many-body problem via the introduction of an exchange-correlation term in the functional of the electronic density
. DFT-calculated bands are in many cases found to be in agreement with experimentally measured bands, for example by angle-resolved photoemission spectroscopy
(ARPES). In particular, the band shape is typically well reproduced by DFT. But there are also systematic errors in DFT bands when compared to experiment results. In particular, DFT seems to systematically underestimate by about 30-40% the band gap in insulators and semiconductors.
It must be said that DFT is, in principle an exact theory to reproduce and predict ground state
properties (e.g., the total energy, the atomic structure, etc.). However, DFT is not a theory to address excited state
properties, such as the band plot of a solid that represents the excitation energies of electrons injected or removed from the system. What in literature is quoted as a DFT band plot is a representation of the DFT Kohn-Sham energies, i.e., the energies of a fictive non-interacting system, the Kohn-Sham system, which has no physical interpretation at all. The Kohn-Sham electronic structure must not be confused with the real, quasiparticle
electronic structure of a system, and there is no Koopman's theorem holding for Kohn-Sham energies, as there is for Hartree-Fock energies, which can be truly considered as an approximation for quasiparticle energies. Hence, in principle, Kohn-Sham based DFT is not a band theory, i.e., not a theory suitable for calculating bands and band-plots. In principle time-dependent DFT
can be used to calculate the true band structure although in practise this is often difficult.
, one can resort to so-called Green's function
methods. Indeed, knowledge of the Green's function of a system provides both ground (the total energy) and also excited state observables of the system. The poles
of the Green's function are the quasiparticle energies, the bands of a solid. The Green's function can be calculated by solving the Dyson equation once the self-energy
of the system is known. For real systems like solids, the self-energy is a very complex quantity and usually approximations are needed to solve the problem. One such approximation is the GW approximation
, so called from the mathematical form the self-energy takes as the product Σ = GW of the Green's function G and the dynamically screened interaction W. This approach is more pertinent when addressing the calculation of band plots (and also quantities beyond, such as the spectral function) and can also be formulated in a completely ab initio way. The GW approximation seems to provide band gaps of insulators and semiconductors in agreement with experiment, and hence to correct the systematic DFT underestimation.
that have an odd number of electrons per unit cell are insulators, in direct conflict with this result. This kind of material is known as a Mott insulator
, and requires inclusion of detailed electron-electron interactions (treated only as an averaged effect on the crystal potential in band theory) to explain the discrepancy. The Hubbard model
is an approximate theory that can include these interactions. It can be treated non-perturbatively within the so-called Dynamical Mean Field Theory
, which bridges the gap between the nearly-free electron approximation and the atomic limit.
The band structure has been generalised to wavevectors that are complex number
s, resulting in what is called a complex band structure, which is of interest at surfaces and interfaces.
Each model describes some types of solids very well, and others poorly. The nearly-free electron model works well for metals, but poorly for non-metals. The tight binding model is extremely accurate for ionic insulators, such as metal halide salts (e.g. NaCl
).
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, the electronic band structure (or simply band structure) of a solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
describes those ranges of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
is "forbidden" or "allowed" to have. Band structure derives from the diffraction
Dynamical theory of diffraction
The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system
Crystal system
In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...
and Bravais lattice. The band structure of a material determines several characteristics, in particular the material's electronic and optical properties.
Why bands occur in materials
The electrons of a single isolated atom occupy atomic orbitalAtomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s, which form a discrete set of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
levels. If several atoms are brought together into a molecule, their atomic orbitals split, as in a coupled oscillation. This produces a number of molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
s proportional to the number of atoms. When a large number of atoms (of order or more) are brought together to form a solid, the number of orbitals becomes exceedingly large. Consequently, the difference in energy between them becomes very small. Thus, in solids the levels form continuous bands of energy rather than the discrete energy levels of the atoms in isolation. However, some intervals of energy contain no orbitals, no matter how many atoms are aggregated, forming band gaps.
Within an energy band, energy levels form a near continuum. First, the separation between energy levels in a solid is comparable with the energy that electrons constantly exchange with phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s (atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
ic vibrations
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
). Second, it is comparable with the energy uncertainty due to the Heisenberg uncertainty principle, for reasonably long intervals of time. As a result, the separation between energy levels is of no consequence.
Several approaches to finding band structure are discussed below.
Basic concepts


Bands have different widths, based upon the properties of the atomic orbitals from which they arise. Also, allowed bands may overlap, producing (for practical purposes) a single large band.
Figure 1 shows a simplified picture of the bands in a solid that allows the three major types of materials to be identified: metals, semiconductors and insulators.
Metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s contain a band that is partly empty and partly filled regardless of temperature. Therefore they have very high conductivity.
The lowermost, almost fully occupied band in an insulator
Electrical insulation
thumb|250px|[[Coaxial Cable]] with dielectric insulator supporting a central coreThis article refers to electrical insulation. For insulation of heat, see Thermal insulation...
or semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
, is called the valence band
Valence band
In solids, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature....
by analogy with the valence electron
Valence electron
In chemistry, valence electrons are the electrons of an atom that can participate in the formation of chemical bonds with other atoms. Valence electrons are the "own" electrons, present in the free neutral atom, that combine with valence electrons of other atoms to form chemical bonds. In a single...
s of individual atoms. The uppermost, almost unoccupied band is called the conduction band
Conduction band
In the solid-state physics field of semiconductors and insulators, the conduction band is the range of electron energies, higher than that of the valence band, sufficient to free an electron from binding with its individual atom and allow it to move freely within the atomic lattice of the material...
because only when electrons are excited to the conduction band can current flow in these materials. The difference between insulators and semiconductors is only that the forbidden band gap
Band gap
In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
between the valence band and conduction band is larger in an insulator, so that fewer electrons are found there and the electrical conductivity is lower. Because one of the main mechanisms for electrons to be excited to the conduction band is due to thermal energy, the conductivity of semiconductors is strongly dependent on the temperature of the material.
This band gap is one of the most useful aspects of the band structure, as it strongly influences the electrical and optical properties of the material. Electrons can transfer from one band to the other by means of carrier generation and recombination
Carrier generation and recombination
In the solid state physics of semiconductors, carrier generation and recombination are processes by which mobile charge carriers are created and eliminated. Carrier generation and recombination processes are fundamental to the operation of many optoelectronic semiconductor devices, such as...
processes. The band gap and defect states created in the band gap by doping can be used to create semiconductor device
Semiconductor device
Semiconductor devices are electronic components that exploit the electronic properties of semiconductor materials, principally silicon, germanium, and gallium arsenide, as well as organic semiconductors. Semiconductor devices have replaced thermionic devices in most applications...
s such as solar cell
Solar cell
A solar cell is a solid state electrical device that converts the energy of light directly into electricity by the photovoltaic effect....
s, diode
Diode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
s, transistor
Transistor
A transistor is a semiconductor device used to amplify and switch electronic signals and power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current...
s, laser diode
Laser diode
The laser diode is a laser where the active medium is a semiconductor similar to that found in a light-emitting diode. The most common type of laser diode is formed from a p-n junction and powered by injected electric current...
s, and others.
Symmetry
A more complete view of the band structure takes into account the periodic nature of a crystal lattice using the symmetry operations that form a space groupSpace group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
. The Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is solved for the crystal, which has Bloch wave
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
s as solutions:
 ,
,where k is called the wavevector, and is related to the direction of motion of the electron in the crystal, and n is the band index, which simply numbers the energy bands. The wavevector k takes on values within the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
(BZ) corresponding to the crystal lattice, and particular directions/points in the BZ are assigned conventional names like Γ, Δ, Λ, Σ, etc. These directions are shown for the face-centered cubic lattice geometry in Figure 2.
The available energies for the electron also depend upon k, as shown in Figure 3 for silicon in the more complex energy band diagram at the right. In this diagram the topmost energy of the valence band is labeled Ev and the bottom energy in the conduction band is labeled Ec. Note that for silicon, the top of the valence band is not directly below the bottom of the conduction band (Ev is for an electron traveling in direction Γ, Ec in direction X), so silicon is called an indirect gap material. For an electron to be excited from the valence band to the conduction band within an indirect gap material, it needs something to give it both energy Ec – Ev and a change in direction/momentum. In other semiconductors (for example III-V materials, such as GaAs) both Ec and Ev are at Γ, and therefore these materials are direct gap materials (no momentum change required). Direct gap materials benefit the operation of semiconductor laser diodes.
Anderson's rule
Anderson's rule
Anderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. It is also referred to as the electron affinity rule. Anderson's rule was first described by R. L...
is used to align band diagrams between two different semiconductors in contact.
Band structures in different types of solids
Although electronic band structures are usually associated with crystalCrystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
line materials, quasi-crystalline and amorphous solid
Amorphous solid
In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal....
s may also exhibit band structures. However, the periodic nature and symmetrical properties of crystalline materials makes it much easier to examine the band structures of these materials theoretically. In addition, the well-defined symmetry axes of crystalline materials makes it possible to determine the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
ship between the momentum (a 3-dimension vector quantity) and energy of a material. As a result, virtually all of the existing theoretical work on the electronic band structure of solids has focused on crystalline materials.
Density of states
While the density of energy statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
in a band could be very large for some materials, it may not be uniform. It approaches zero at the band boundaries, and is generally highest near the middle of a band.
The density of states for the free electron model
Free electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
in three dimensions is given by,

Filling of bands
Although the number of states in all of the bands is effectively infinite, in an uncharged material the number of electrons is equal only to the number of protons in the atoms of the material. Therefore not all of the states are occupied by electrons ("filled") at any time. The likelihood of any particular state being filled at any temperature is given by Fermi-Dirac statisticsFermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
. The probability is given by the following expression:

where:
- kB is Boltzmann's constant,
- T is the temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, - µ is the chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
(in semiconductor physics, this quantity is more often called the "Fermi levelFermi levelThe Fermi level is a hypothetical level of potential energy for an electron inside a crystalline solid. Occupying such a level would give an electron a potential energy \epsilon equal to its chemical potential \mu as they both appear in the Fermi-Dirac distribution function,which...
" and denoted EF).
The Fermi level naturally is the level at which the electrons and protons are balanced.
At T=0, the distribution is a simple step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
:

At nonzero temperatures, the step "smooths out", so that an appreciable number of states below the Fermi level are empty, and some states above the Fermi level are filled.
Theory of band structures in crystals
The ansatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
is the special case of electron waves in a periodic crystal lattice using Bloch waves as treated generally in the dynamical theory of diffraction
Dynamical theory of diffraction
The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
. Every crystal is a periodic structure which can be characterized by a Bravais lattice, and for each Bravais lattice we can determine the reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
, which encapsulates the periodicity in a set of three reciprocal lattice vectors (b1,b2,b3). Now, any periodic potential V(r) which shares the same periodicity as the direct lattice can be expanded out as a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
whose only non-vanishing components are those associated with the reciprocal lattice vectors. So the expansion can be written as:

where K = m1b1 + m2b2 + m3b3 for any set of integers (m1,m2,m3).
From this theory, an attempt can be made to predict the band structure of a particular material, however most ab initio methods for electronic structure calculations fail to predict the observed band gap.
Nearly free electron approximation
In the nearly free electron approximation, interactions between electrons are completely ignored. This approximation allows use of Bloch's TheoremBloch's theorem
* For the theorem named after Felix Bloch on wave functions of a particle in a periodic potential, see Bloch wave.* For the theorem in complex variables named after André Bloch, see Bloch's theorem ....
which states that electrons in a periodic potential have wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s and energies which are periodic in wavevector up to a constant phase shift between neighboring reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vectors. The consequences of periodicity are described mathematically by the Bloch wavefunction:

where the function
 is periodic over the crystal lattice, that is,
is periodic over the crystal lattice, that is, .
.Here index n refers to the n-th energy band, wavevector k is related to the direction of motion of the electron, r is position in the crystal, and R is location of an atomic site.
The NFE model works particularly well in materials like metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s where distances between neighbouring atoms are small. In such materials
the overlap of atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s and potentials on neighbouring atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s is relatively large. In that case the wave function of the electron can be approximated by a (modified) plane wave. The band structure of a metal like Aluminum even gets close to the Empty Lattice Approximation
Empty Lattice Approximation
The Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
.
Tight-binding model
The opposite extreme to the nearly-free electron approximation assumes the electrons in the crystal behave much like an assembly of constituent atoms. This tight-binding model assumes the solution to the time-independent single electron Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
 is well approximated by a linear combination
is well approximated by a linear combinationLinear combination of atomic orbitals molecular orbital method
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions...
of atomic orbitals
 .
. ,
,where the coefficients
 are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by:
are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by: ;
;in which
 is the periodic part of the Bloch wave and the integral is over the Brillouin zone
is the periodic part of the Bloch wave and the integral is over the Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. Here index n refers to the n-th energy band in the crystal. The Wannier functions are localized near atomic sites, like atomic orbitals, but being defined in terms of Bloch functions they are accurately related to solutions based upon the crystal potential. Wannier functions on different atomic sites R are orthogonal. The Wannier functions can be used to form the Schrödinger solution for the n-th energy band as:
 .
.The TB model works well in materials with limited overlap between atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s and potentials on neighbouring atoms. Band structures of materials like Si
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
, GaAs
Gaas
Gaas is a commune in the Landes department in Aquitaine in south-western France....
, SiO2 and diamond
Diamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
for instance are well described by TB-Hamiltonians on the basis of atomic sp3 orbitals. In transition metals a mixed TB-NFE model is used to describe the broad NFE conduction band
Conduction band
In the solid-state physics field of semiconductors and insulators, the conduction band is the range of electron energies, higher than that of the valence band, sufficient to free an electron from binding with its individual atom and allow it to move freely within the atomic lattice of the material...
and the narrow embedded TB d-bands. The radial functions of
the atomic orbital part
of the Wannier functions are most easily calculated by the use of pseudopotential
Pseudopotential
In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering.- Atomic physics :...
methods. NFE, TB or combined NFE-TB band structure
calculations,
sometimes extended with wave function approximations based on pseudopotential methods, are often used as an economic starting point for further calculations.
KKR model
The simplest form of this approximation centers non-overlapping spheres (referred to as muffin tins) on the atomic positions. Within these regions, the potential experienced by an electron is approximated to be spherically symmetric about the given nucleus. In the remaining interstitial region, the screened potentialScreening effect
In solids, especially in metals and semiconductors, the electrostatic screening or screening effect reduces the electrostatic field and Coulomb potential of an ion inside the solid...
is approximated as a constant. Continuity of the potential between the atom-centered spheres and interstitial region is enforced.
A variational implementation was suggested by Korringa and by Kohn
Walter Kohn
Walter Kohn is an Austrian-born American theoretical physicist.He was awarded, with John Pople, the Nobel Prize in chemistry in 1998. The award recognized their contributions to the understandings of the electronic properties of materials...
and Rostocker, and is often referred to as the KKR model
Coherent Potential Approximation
The coherent potential approximation is a method, in physics, of finding the Green's function of an effective medium. It is a useful concept in understanding how waves scatter in a material which displays spatial inhomogeneity....
.
Order-N spectral methods
To quote RP Martin: "The concept of localization can be imbedded directly into the methods of electronic structure to create algorithms that take advantage of locality … For large systems, this fact can be used to make "order-N" or O(N) methods where the computational time scales linearly in the size of the system".Density-functional theory
In recent physics literature, a large majority of the electronic structures and band plots are calculated using density-functional theory (DFT), which is not a model but rather a theory, i.e., a microscopic first-principles theory of condensed matter physicsCondensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
that tries to cope with the electron-electron many-body problem via the introduction of an exchange-correlation term in the functional of the electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
. DFT-calculated bands are in many cases found to be in agreement with experimentally measured bands, for example by angle-resolved photoemission spectroscopy
Photoemission spectroscopy
Photoemission spectroscopy , also known as photoelectron spectroscopy, refers to energy measurement of electrons emitted from solids, gases or liquids by the photoelectric effect, in order to determine the binding energies of electrons in a substance...
(ARPES). In particular, the band shape is typically well reproduced by DFT. But there are also systematic errors in DFT bands when compared to experiment results. In particular, DFT seems to systematically underestimate by about 30-40% the band gap in insulators and semiconductors.
It must be said that DFT is, in principle an exact theory to reproduce and predict ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
properties (e.g., the total energy, the atomic structure, etc.). However, DFT is not a theory to address excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
properties, such as the band plot of a solid that represents the excitation energies of electrons injected or removed from the system. What in literature is quoted as a DFT band plot is a representation of the DFT Kohn-Sham energies, i.e., the energies of a fictive non-interacting system, the Kohn-Sham system, which has no physical interpretation at all. The Kohn-Sham electronic structure must not be confused with the real, quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
electronic structure of a system, and there is no Koopman's theorem holding for Kohn-Sham energies, as there is for Hartree-Fock energies, which can be truly considered as an approximation for quasiparticle energies. Hence, in principle, Kohn-Sham based DFT is not a band theory, i.e., not a theory suitable for calculating bands and band-plots. In principle time-dependent DFT
Time-dependent density functional theory
Time-dependent density functional theory is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields...
can be used to calculate the true band structure although in practise this is often difficult.
Green's function methods and the ab initio GW approximation
To calculate the bands including electron-electron interaction many-body effectsMany-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
, one can resort to so-called Green's function
Green's function (many-body theory)
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
methods. Indeed, knowledge of the Green's function of a system provides both ground (the total energy) and also excited state observables of the system. The poles
Poles
thumb|right|180px|The state flag of [[Poland]] as used by Polish government and diplomatic authoritiesThe Polish people, or Poles , are a nation indigenous to Poland. They are united by the Polish language, which belongs to the historical Lechitic subgroup of West Slavic languages of Central Europe...
of the Green's function are the quasiparticle energies, the bands of a solid. The Green's function can be calculated by solving the Dyson equation once the self-energy
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
of the system is known. For real systems like solids, the self-energy is a very complex quantity and usually approximations are needed to solve the problem. One such approximation is the GW approximation
GW approximation
The GW approximation is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green function G and the screened Coulomb interaction W can be truncated after the...
, so called from the mathematical form the self-energy takes as the product Σ = GW of the Green's function G and the dynamically screened interaction W. This approach is more pertinent when addressing the calculation of band plots (and also quantities beyond, such as the spectral function) and can also be formulated in a completely ab initio way. The GW approximation seems to provide band gaps of insulators and semiconductors in agreement with experiment, and hence to correct the systematic DFT underestimation.
Mott insulators
Although the nearly-free electron approximation is able to describe many properties of electron band structures, one consequence of this theory is that it predicts the same number of electrons in each unit cell. If the number of electrons is odd, we would then expect that there is an unpaired electron in each unit cell, and thus that the valence band is not fully occupied, making the material a conductor. However, materials such as CoOCobalt(II) oxide
Cobalt oxide or cobalt monoxide is an inorganic compound that appears as olive-green to red crystals, or as a greyish or black powder...
that have an odd number of electrons per unit cell are insulators, in direct conflict with this result. This kind of material is known as a Mott insulator
Mott insulator
Mott insulators are a class of materials that should conduct electricity under conventional band theories, but are insulators when measured...
, and requires inclusion of detailed electron-electron interactions (treated only as an averaged effect on the crystal potential in band theory) to explain the discrepancy. The Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
is an approximate theory that can include these interactions. It can be treated non-perturbatively within the so-called Dynamical Mean Field Theory
Dynamical mean field theory
Dynamical Mean Field Theory is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in Density Functional Theory and usual band structure calculations, breaks down...
, which bridges the gap between the nearly-free electron approximation and the atomic limit.
Augmented plane waves
John Clarke Slater and members of his Solid State and Molecular Theory Group in the Physics Department at MIT, comprised one of the main research centers for the calculation of band structures. John Wood played a very strong role in large scale computations using the augmented plane wave (APW) method.Others
Calculating band structures is an important topic in theoretical solid state physics. In addition to the models mentioned above, other models include the following:- k·p perturbation theoryK·p perturbation theoryIn solid-state physics, k·p perturbation theory is an approximation scheme for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method"...
is a technique that allows a band structure to be approximately described in terms of just a few parameters. The technique is commonly used for semiconductors, and the parameters in the model are often determined by experiment. - The Kronig-Penney Model, a one-dimensional rectangular well model useful for illustration of band formation. While simple, it predicts many important phenomena, but is not quantitative.
- Bands may also be viewed as the large-scale limit of molecular orbital theoryMolecular orbital theoryIn chemistry, molecular orbital theory is a method for determining molecular structure in which electrons are not assigned to individual bonds between atoms, but are treated as moving under the influence of the nuclei in the whole molecule...
. A solid creates a large number of closely spaced molecular orbitals, which appear as a band. - Hubbard modelHubbard modelThe Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
The band structure has been generalised to wavevectors that are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, resulting in what is called a complex band structure, which is of interest at surfaces and interfaces.
Each model describes some types of solids very well, and others poorly. The nearly-free electron model works well for metals, but poorly for non-metals. The tight binding model is extremely accurate for ionic insulators, such as metal halide salts (e.g. NaCl
Sodium chloride
Sodium chloride, also known as salt, common salt, table salt or halite, is an inorganic compound with the formula NaCl. Sodium chloride is the salt most responsible for the salinity of the ocean and of the extracellular fluid of many multicellular organisms...
).
Further reading
- Microelectronics, by Jacob Millman and Arvin Gabriel, ISBN 0-07-463736-3, Tata McGraw-Hill Edition.
- Solid State Physics, by Neil Ashcroft and N. David Mermin, ISBN 0-03-083993-9
- Elementary Solid State Physics: Principles and Applications, by M. Ali Omar, ISBN 0-201-60733-6
- Electronic and Optoelectronic Properties of Semiconductor Structures - Chapter 2 and 3 by Jasprit Singh, ISBN 0-521-82379-X
- Electronic Structure: Basic Theory and Practical Methods by Richard Martin, ISBN 978-052178285
- Condensed Matter Physics by Michael P. Marder, ISBN 0-471-17779-2
- Computational Methods in Solid State Physics by V V Nemoshkalenko and N.V. Antonov, ISBN 90-5699-094-2
- Elementary Electronic Structure by Walter A. Harrison, ISBN 981-238-708-0
- Pseudopotentials in the theory of metals by Walter A. Harrison, W.A. Benjamin (New York) 1966
- Tutorial on Bandstructure Methods by Dr. Vasileska(2008)
See also
- Bloch waves
- Nearly-free electron modelNearly-free electron modelIn solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
- Free electron modelFree electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
- Empty Lattice ApproximationEmpty Lattice ApproximationThe Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
- Fermi gasFermi gasA Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
- Fermi surfaceFermi surfaceIn condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
- Band GapBand gapIn solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
- Effective mass
- k·p methodK·p perturbation theoryIn solid-state physics, k·p perturbation theory is an approximation scheme for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method"...
- Local-density approximationLocal-density approximationLocal-density approximations are a class of approximations to the exchange-correlation energy functional in density functional theory that depend solely upon the value of the electronic density at each point in space . Many approaches can yield local approximations to the XC energy...
- Dynamical theory of diffractionDynamical theory of diffractionThe dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
- Solid state physics
- Kronig-Penney model
- Anderson's ruleAnderson's ruleAnderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. It is also referred to as the electron affinity rule. Anderson's rule was first described by R. L...
- Dynamical Mean Field TheoryDynamical mean field theoryDynamical Mean Field Theory is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in Density Functional Theory and usual band structure calculations, breaks down...

