Empty Lattice Approximation
Encyclopedia
The Empty Lattice Approximation is a theoretical electronic band structure
model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons
that move through a crystal lattice
. The energy of the electrons in the "empty lattice" is the same as the energy of free electrons. The model is useful because it clearly illustrates a number of, the sometimes very complex, features of energy dispersion relations in solids which are fundamental to all electronic band structures.
of the system. Topologically defined parameters, like scattering
cross sections
, depend on the magnitude of the potential and the size of the potential well
. For 1, 2 and 3-dimensional spaces potential wells do always scatter waves, no matter how small their potentials are, what their signs are or how limited their sizes are. For a particle in a one-dimensional lattice, like the Kronig-Penney model, it is possible to calculate the band structure analytically by substituting the values for the potential, the lattice spacing and the size of potential well. For two and three-dimensional problems it is more difficult to calculate a band structure based on a similar model with a few parameters accurately. Nevertheless the properties of the band structure can easily be approximated in most regions by perturbation methods
.
In theory the lattice is infinitely large, so a weak periodic scattering potential will eventually be strong enough to reflect the wave. The scattering process results in the well known Bragg reflections
of electrons by the periodic potential of the crystal structure
. This is the origin of the periodicity of the dispersion relation and the division of k-space
in Brillouin zones. The periodic energy dispersion relation is expressed
as: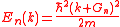
The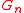
are the reciprocal lattice
vectors to which the bands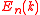
belong. Electrons with wave vectors outside the first Brillouin zone
are scattered by the lattice and mapped back into the first Brillouin zone by a so called Umklapp process
.
The figure on the right shows the dispersion relation for three periods in reciprocal space of a one-dimensional lattice with lattice cells of length a.
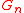that determine the bands in an energy interval is limited to two when the energy rises. In two and three dimensional lattices the number of reciprocal lattice vectors that determine the free electron bands 
increases more rapidly when the length of the wave vector increases and the energy rises. This is because the number of reciprocal lattice vectors 
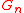that lie in an interval 
increases. The density of states
in an energy interval
depends on the number of states in an interval 
in reciprocal space and the slope of the dispersion relation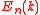 
.
Though the lattice cells are not spherically symmetric, the dispersion relation still has spherical symmetry from the point of view of a fixed central point in a reciprocal lattice cell if the dispersion relation is extended outside the central Brillouin zone. The density of states in a three-dimensional lattice will be the same as in the case of the absence of a lattice. For the three-dimensional case the density of state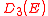s
is;
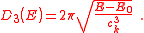
In three-dimensional space the Brillouin zone boundaries are planes. The dispersion relations show conics of the free-electron energy dispersion parabolas for all possible reciprocal lattice vectors. This results in a very complicated set intersecting of curves when the dispersion relations are calculated because there is a large number of possible angles between evaluation trajectories, first and higher order Brillouin zone boundaries and dispersion parabola intersection cones.
.svg.png)
"Free electrons" that move through the lattice of a solid with wave vectors 
far outside the first Brillouin zone are still reflected back into the first Brillouin zone. See the external links section for sites with examples and figures.
, like aluminium
, the screening effect
strongly reduces the electric field of the ions in the solid. The electrostatic potential is expressed as
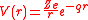
where Z is the atomic number
, e is the elementary unit charge, r is the distance to the nucleus of the embedded ion and q is a screening parameter that determines the range of the potential. The Fourier transform
,
, of the lattice potential, 
, is expressed as
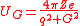
When the values of the off-diagonal elements
between the reciprocal lattice vectors in the Hamiltonian almost go to zero. As a result the magnitude of the band gap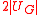 
collapses and the Empty Lattice Approximation is obtained.
s crystallize in three kinds of crystal structures: the BCC and FCC cubic crystal structures
and the hexagonal
close-packed HCP crystal structure.
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons
Free electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
that move through a crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. The energy of the electrons in the "empty lattice" is the same as the energy of free electrons. The model is useful because it clearly illustrates a number of, the sometimes very complex, features of energy dispersion relations in solids which are fundamental to all electronic band structures.
Scattering and periodicity
The periodic potential of the lattice in this free electron model must be weak because otherwise the electrons wouldn't be free. The strength of the scattering mainly depends on the geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
of the system. Topologically defined parameters, like scattering
Scattering cross-section
The scattering cross-section, σscat, is a hypothetical area which describes the likelihood of light being scattered by a particle. In general, the scattering cross-section is different from the geometrical cross-section of a particle, and it depends upon the wavelength of light and the...
cross sections
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
, depend on the magnitude of the potential and the size of the potential well
Potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
. For 1, 2 and 3-dimensional spaces potential wells do always scatter waves, no matter how small their potentials are, what their signs are or how limited their sizes are. For a particle in a one-dimensional lattice, like the Kronig-Penney model, it is possible to calculate the band structure analytically by substituting the values for the potential, the lattice spacing and the size of potential well. For two and three-dimensional problems it is more difficult to calculate a band structure based on a similar model with a few parameters accurately. Nevertheless the properties of the band structure can easily be approximated in most regions by perturbation methods
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
.
In theory the lattice is infinitely large, so a weak periodic scattering potential will eventually be strong enough to reflect the wave. The scattering process results in the well known Bragg reflections
Bragg's law
In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave...
of electrons by the periodic potential of the crystal structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. This is the origin of the periodicity of the dispersion relation and the division of k-space
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
in Brillouin zones. The periodic energy dispersion relation is expressed
as:
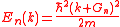
The
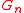are the reciprocal latticeReciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
vectors to which the bands
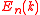belong. Electrons with wave vectors outside the first Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
are scattered by the lattice and mapped back into the first Brillouin zone by a so called Umklapp process
Umklapp scattering
Umklapp scattering is the transformation, like a reflection or a translation, of a wave vector to another Brillouin zone as a result of a scattering process, for example an electron-lattice potential scattering or an anharmonic phonon-phonon scattering process, reflecting an electronic state or...
.
The figure on the right shows the dispersion relation for three periods in reciprocal space of a one-dimensional lattice with lattice cells of length a.
The energy bands and the density of states
In a one-dimensional lattice the number of reciprocal lattice vectors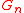 that determine the bands in an energy interval is limited to two when the energy rises. In two and three dimensional lattices the number of reciprocal lattice vectors that determine the free electron bands increases more rapidly when the length of the wave vector increases and the energy rises. 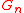This is because the number of reciprocal lattice vectors that lie in an interval increases. The density of statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
in an energy interval
depends on the number of states in an interval in reciprocal space and the slope of the dispersion relation 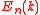.Though the lattice cells are not spherically symmetric, the dispersion relation still has spherical symmetry from the point of view of a fixed central point in a reciprocal lattice cell if the dispersion relation is extended outside the central Brillouin zone. The density of states in a three-dimensional lattice will be the same as in the case of the absence of a lattice. For the three-dimensional case the density of states
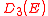is;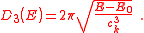In three-dimensional space the Brillouin zone boundaries are planes. The dispersion relations show conics of the free-electron energy dispersion parabolas for all possible reciprocal lattice vectors. This results in a very complicated set intersecting of curves when the dispersion relations are calculated because there is a large number of possible angles between evaluation trajectories, first and higher order Brillouin zone boundaries and dispersion parabola intersection cones.
Second, third and higher Brillouin zones
far outside the first Brillouin zone are still reflected back into the first Brillouin zone. See the external links section for sites with examples and figures.The nearly free electron model
In most simple metalsMetal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
, like aluminium
Aluminium
Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances....
, the screening effect
Screening effect
In solids, especially in metals and semiconductors, the electrostatic screening or screening effect reduces the electrostatic field and Coulomb potential of an ion inside the solid...
strongly reduces the electric field of the ions in the solid. The electrostatic potential is expressed as
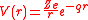
where Z is the atomic number
Atomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
, e is the elementary unit charge, r is the distance to the nucleus of the embedded ion and q is a screening parameter that determines the range of the potential. The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
,
, of the lattice potential, , is expressed as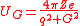When the values of the off-diagonal elements
between the reciprocal lattice vectors in the Hamiltonian almost go to zero. As a result the magnitude of the band gap 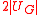collapses and the Empty Lattice Approximation is obtained.The crystal structures of metals
Apart from a few exotic exceptions, metalMetal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s crystallize in three kinds of crystal structures: the BCC and FCC cubic crystal structures
Cubic crystal system
In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals....
and the hexagonal
Hexagonal crystal system
In crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families...
close-packed HCP crystal structure.