Local-density approximation
Encyclopedia
Local-density approximations (LDA) are a class of approximations to the exchange
-correlation (XC) energy functional
in density functional theory
(DFT) that depend solely upon the value of the electronic density
at each point in space (and not, for example, derivatives of the density or the Kohn-Sham orbitals
). Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems (molecules and solids).
In general, for a spin-unpolarized system, a local-density approximation for the exchange-correlation energy is written as
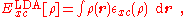
where ρ is the electronic density
and εxc, the exchange-correlation energy density, is a function of the density alone. The exchange-correlation energy is decomposed into exchange and correlation terms linearly,
so that separate expressions for Ex and Ec are sought. The exchange term takes on a simple analytic form for the HEG. Only limiting expressions for the correlation density are known exactly, leading to numerous different approximations for εc.
Local-density approximations are important in the construction of more sophisticated approximations to the exchange-correlation energy, such as generalized gradient approximations or hybrid functional
s, as a desirable property of any approximate exchange-correlation functional is that it reproduce the exact results of the HEG for non-varying densities. As such, LDA's are often an explicit component of such functionals.
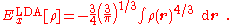
and the low limit
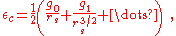
where the Wigner-Seitz radius is related to the density as
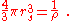
Accurate quantum Monte Carlo
simulations for the energy of the HEG have been performed for several intermediate values of the density, in turn providing accurate values of the correlation energy density. The most popular LDA's to the correlation energy density interpolate these accurate values obtained from simulation while reproducing the exactly known limiting behavior. Various approaches, using different analytic forms for εc, have generated several LDA's for the correlation functional, including
Predating these, and even the formal foundations of DFT itself, is the Wigner correlation functional obtained perturbatively from the HEG model.
systems is straightforward for exchange, where the exact spin-scaling is known, but for correlation further approximations must be employed. A spin polarized system in DFT employs two spin-densities, ρα and ρβ with ρ = ρα + ρβ, and the form of the local-spin-density approximation (LSDA) is
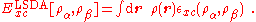
For the exchange energy, the exact result (not just for local density approximations) is known in terms of the spin-unpolarized functional:
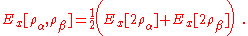
The spin-dependence of the correlation energy density is approached by introducing the relative spin-polarization:
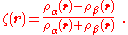
corresponds to the paramagnetic spin-unpolarized situation with equal
and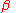 
spin densities whereas 
corresponds to the ferromagnetic situation where one spin density vanishes. The spin correlation energy density for a given values of the total density and relative polarization, εc(ρ,ς), is constructed so to interpolate the extreme values. Several forms have been developed in conjunction with LDA correlation functionals.
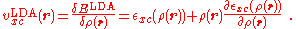
In finite systems, the LDA potential decays asymptotically with an exponential form. This is in error; the true exchange-correlation potential decays much slower in a Coulombic manner. The artificially rapid decay manifests itself in the number of Kohn-Sham orbitals the potential can bind (that is, how many orbitals have energy less than zero). The LDA potential can not support a Rydberg series and those states it does bind are too high in energy. This results in the HOMO
energy being too high in energy, so that any predictions for the ionization potential
based on Koopman's theorem are poor. Further, the LDA provides a poor description of electron-rich species such as anions where it is often unable to bind an additional electron, erroneously predicating species to be unstable.
Exchange interaction
In physics, the exchange interaction is a quantum mechanical effect without classical analog which increases or decreases the expectation value of the energy or distance between two or more identical particles when their wave functions overlap...
-correlation (XC) energy functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
in density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
(DFT) that depend solely upon the value of the electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
at each point in space (and not, for example, derivatives of the density or the Kohn-Sham orbitals
Kohn-Sham equations
In quantum chemistry, specifically density functional theory, the Kohn–Sham equation is the Schrödinger equation of a fictitious system of non-interacting particles that generate the same density as any given system of interacting particles...
). Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems (molecules and solids).
In general, for a spin-unpolarized system, a local-density approximation for the exchange-correlation energy is written as
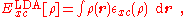
where ρ is the electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
and εxc, the exchange-correlation energy density, is a function of the density alone. The exchange-correlation energy is decomposed into exchange and correlation terms linearly,
so that separate expressions for Ex and Ec are sought. The exchange term takes on a simple analytic form for the HEG. Only limiting expressions for the correlation density are known exactly, leading to numerous different approximations for εc.
Local-density approximations are important in the construction of more sophisticated approximations to the exchange-correlation energy, such as generalized gradient approximations or hybrid functional
Hybrid functional
Hybrid functionals are a class of approximations to the exchange-correlation energy functional in density functional theory that incorporate a portion of exact exchange from Hartree-Fock theory with exchange and correlation from other sources...
s, as a desirable property of any approximate exchange-correlation functional is that it reproduce the exact results of the HEG for non-varying densities. As such, LDA's are often an explicit component of such functionals.
Homogeneous electron gas
Approximation for εxc depending only upon the density can be developed in numerous ways. The most successful approach is based on the homogeneous electron gas. This is constructed by placing N interacting electrons in to a volume, V, with a positive background charge keeping the system neutral. N and V are then taken to infinity in the manner that keeps the density (ρ = N / V) finite. This is a useful approximation as the total energy consists of contributions only from the kinetic energy and exchange-correlation energy, and that the wavefunction is expressible in terms of planewaves. In particular, for a constant density ρ, the exchange energy density is proportional to ρ⅓.Exchange functional
The exchange-energy density of a HEG is known analytically. The LDA for exchange employs this expression under the approximation that the exchange-energy in a system where the density in not homogeneous, is obtained by applying the HEG results pointwise, yielding the expression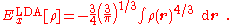Correlation functional
Analytic expressions for the correlation energy of the HEG are not known except in the high- and low-density limits corresponding to infinitely-weak and infinitely-strong correlation. For a HEG with density ρ, the high-density limit of the correlation energy density isand the low limit
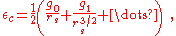
where the Wigner-Seitz radius is related to the density as
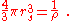
Accurate quantum Monte Carlo
Quantum Monte Carlo
Quantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
simulations for the energy of the HEG have been performed for several intermediate values of the density, in turn providing accurate values of the correlation energy density. The most popular LDA's to the correlation energy density interpolate these accurate values obtained from simulation while reproducing the exactly known limiting behavior. Various approaches, using different analytic forms for εc, have generated several LDA's for the correlation functional, including
- Vosko-Wilk-Nusair (VWN)
- Perdew-Zunger (PZ81)
- Cole-Perdew (CP)
- Perdew-Wang (PW92)
Predating these, and even the formal foundations of DFT itself, is the Wigner correlation functional obtained perturbatively from the HEG model.
Spin polarization
The extension of density functionals to spin-polarizedSpin polarization
Spin polarization is the degree to which the spin, i.e., the intrinsic angular momentum of elementary particles, is aligned with a given direction. This property may pertain to the spin, hence to the magnetic moment, of conduction electrons in ferromagnetic metals, such as iron, giving rise to...
systems is straightforward for exchange, where the exact spin-scaling is known, but for correlation further approximations must be employed. A spin polarized system in DFT employs two spin-densities, ρα and ρβ with ρ = ρα + ρβ, and the form of the local-spin-density approximation (LSDA) is
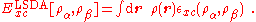
For the exchange energy, the exact result (not just for local density approximations) is known in terms of the spin-unpolarized functional:
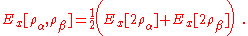
The spin-dependence of the correlation energy density is approached by introducing the relative spin-polarization:
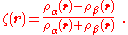
corresponds to the paramagnetic spin-unpolarized situation with equal and 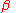spin densities whereas corresponds to the ferromagnetic situation where one spin density vanishes. The spin correlation energy density for a given values of the total density and relative polarization, εc(ρ,ς), is constructed so to interpolate the extreme values. Several forms have been developed in conjunction with LDA correlation functionals.Exchange-correlation potential
The exchange-correlation potential corresponding to the exchange-correlation energy for a local density approximation is given by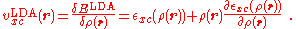In finite systems, the LDA potential decays asymptotically with an exponential form. This is in error; the true exchange-correlation potential decays much slower in a Coulombic manner. The artificially rapid decay manifests itself in the number of Kohn-Sham orbitals the potential can bind (that is, how many orbitals have energy less than zero). The LDA potential can not support a Rydberg series and those states it does bind are too high in energy. This results in the HOMO
Homo
Homo may refer to:*the Greek prefix ὅμο-, meaning "the same"*the Latin for man, human being*Homo, the taxonomical genus including modern humans...
energy being too high in energy, so that any predictions for the ionization potential
Ionization potential
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
based on Koopman's theorem are poor. Further, the LDA provides a poor description of electron-rich species such as anions where it is often unable to bind an additional electron, erroneously predicating species to be unstable.