Electronic density
Encyclopedia
In quantum mechanics
, and in particular quantum chemistry
, the electronic density is a measure of the probability of an electron
occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either ρ(r) or n(r). The density is determined, through definition, by the normalized N-electron wavefunction
which itself depends upon 4N variables (3N spatial and N spin
coordinates). Conversely, the density determines the wave function modulo a phase factor, providing the formal foundation of density functional theory
.
(with r and s denoting spatial and spin variables respectively) is defined as
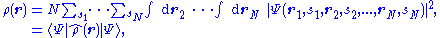
where the operator corresponding to the density observable is
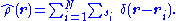
In Hartree-Fock
and density functional
theories the wave function is typically represented as a single Slater determinant
constructed from N orbitals, φk, with corresponding occupations nk. In these situations the density simplifies to
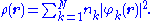
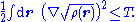
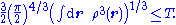
For finite kinetic energies, the first (stronger) inequality places the square root of the density in the Sobolev space
H1(R3). Together with the normalization and non-negativity this defines a space containing physically acceptable densities as
The second inequality places the density in the L3 space
. Together with the normalization property places acceptable densities within the intersection of L1 and L3 – a superset of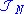
.
electronic density of an atom
is conjectured to be a monotonically
decaying function of the distance from the nucleus
.
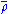, about any given nucleus as
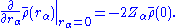
That is, the radial derivative of the spherically averaged density, evaluated at any nucleus, is equal to twice the density at that nucleus multiplied by the negative of the atomic number
(Z).
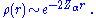
The long-range (large r) behavior of the density is also known, taking the form
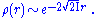
where I is the ionization energy
of the system.
with any spin-free, one-electron operator yields the associated property defined as the derivative of the energy.
For example, a dipole moment is the derivative of the energy with respect to an external magnetic field and
is not the expectation value of the operator over the wavefunction. For some theories they are the same when
the wavefunction is converged. The occupation numbers are not limited to the range of zero to two, and therefore
sometimes even the response density can be negative in certain regions of space.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, and in particular quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, the electronic density is a measure of the probability of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either ρ(r) or n(r). The density is determined, through definition, by the normalized N-electron wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
which itself depends upon 4N variables (3N spatial and N spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
coordinates). Conversely, the density determines the wave function modulo a phase factor, providing the formal foundation of density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
.
Definition
The electronic density corresponding to a normalized N-electron wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
(with r and s denoting spatial and spin variables respectively) is defined as
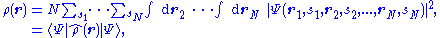
where the operator corresponding to the density observable is
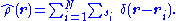
In Hartree-Fock
Hartree-Fock
In computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
and density functional
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
theories the wave function is typically represented as a single Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
constructed from N orbitals, φk, with corresponding occupations nk. In these situations the density simplifies to
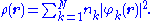
General Properties
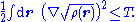
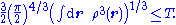
From its definition, the electron density is a non-negative function integrating to the total number of electrons. Further, for a system with kinetic energy T, the density satisfies the inequalitiesFor finite kinetic energies, the first (stronger) inequality places the square root of the density in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
H1(R3). Together with the normalization and non-negativity this defines a space containing physically acceptable densities as
The second inequality places the density in the L3 space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Together with the normalization property places acceptable densities within the intersection of L1 and L3 – a superset of
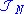.Topology
The ground stateGround state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
electronic density of an atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
is conjectured to be a monotonically
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
decaying function of the distance from the nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
.
Nuclear cusp condition
The electronic density displays cusps at each nucleus in a molecule as a result of the unbounded electron-nucleus Coulomb potential. This behavior is quantified by the Kato cusp condition formulated in terms of the spherically averaged density,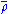, about any given nucleus as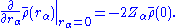That is, the radial derivative of the spherically averaged density, evaluated at any nucleus, is equal to twice the density at that nucleus multiplied by the negative of the atomic number
Atomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
(Z).
Asymptotic behavior
The nuclear cusp condition provides the near-nuclear (small r) density behavior as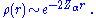The long-range (large r) behavior of the density is also known, taking the form
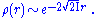
where I is the ionization energy
Ionization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
of the system.
Response Density
Another more-general definition of a density is the "linear-response density". This is the density that when contractedwith any spin-free, one-electron operator yields the associated property defined as the derivative of the energy.
For example, a dipole moment is the derivative of the energy with respect to an external magnetic field and
is not the expectation value of the operator over the wavefunction. For some theories they are the same when
the wavefunction is converged. The occupation numbers are not limited to the range of zero to two, and therefore
sometimes even the response density can be negative in certain regions of space.