Convergence problem
Encyclopedia
In the analytic theory
of continued fractions
, the convergence problem is the determination of conditions on the partial numerators ai and partial denominators bi that are sufficient to guarantee the convergence of the continued fraction
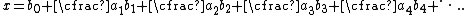
This convergence problem for continued fractions is inherently more difficult (and also more interesting) than the corresponding convergence problem for infinite series.
s, the determinant formula
can easily be applied to demonstrate when the continued fraction converges. Since the denominators Bn cannot be zero in this simple case, the problem boils down to showing that the product of successive denominators BnBn+1 grows more quickly than the product of the partial numerators a1a2a3...an+1. The convergence problem is much more difficult when the elements of the continued fraction are complex number
s.
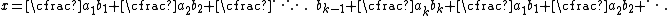
where k ≥ 1, the sequence of partial numerators {a1, a2, a3, ..., ak} contains no values equal to zero, and the partial numerators {a1, a2, a3, ..., ak} and partial denominators {b1, b2, b3, ..., bk} repeat over and over again, ad infinitum.
By applying the theory of linear fractional transformations to
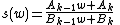
where Ak-1, Bk-1, Ak, and Bk are the numerators and denominators of the k-1st and kth convergents of the infinite periodic continued fraction x, it can be shown that x converges to one of the fixed points of s(w) if it converges at all. Specifically, let r1 and r2 be the roots of the quadratic equation
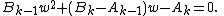
These roots are the fixed points
of s(w). If r1 and r2 are finite then the infinite periodic continued fraction x converges if and only if
If the denominator Bk-1 is equal to zero then an infinite number of the denominators Bnk-1 also vanish, and the continued fraction does not converge to a finite value. And when the two roots r1 and r2 are equidistant from the k-1st convergent – or when r1 is closer to the k-1st convergent than r2 is, but one of the first k convergents equals r2 – the continued fraction x diverges by oscillation.
where b ≠ 0, we can obtain a very strong result. First, by applying an equivalence transformation we see that x converges if and only if
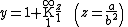
converges. Then, by applying the more general result obtained above it can be shown that
converges for every complex number z except when z is a negative real number and z < −¼. Moreover, this continued fraction y converges to the particular value of
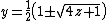
that has the larger absolute value (except when z is real and z < −¼, in which case the two fixed points of the LFT generating y have equal moduli and y diverges by oscillation).
By applying another equivalence transformation the condition that guarantees convergence of
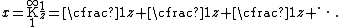
can also be determined. Since a simple equivalence transformation shows that
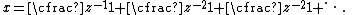
whenever z ≠ 0, the preceding result for the continued fraction y can be restated for x. The infinite periodic continued fraction
converges if and only if z2 is not a real number lying in the interval −4 < z2 ≤ 0 – or, equivalently, x converges if and only if z ≠ 0 and z is not a pure imaginary number lying in the interval −2i < z < 2i.
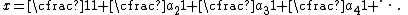
it can be shown that the following statements hold if |ai| ≤ ¼ for the partial numerators ai, i = 2, 3, 4, ...
The proof of the first statement, by Julius Worpitzky in 1865, is apparently the oldest published proof that a continued fraction with complex elements actually converges.
Because the proof of Worpitzky's theorem employs Euler's continued fraction formula to construct an infinite series that is equivalent to the continued fraction x, and the series so constructed is absolutely convergent, the Weierstrass M-test can be applied to a modified version of x. If
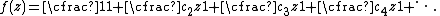
and a positive real number M exists such that |ci| ≤ M (i = 2, 3, 4, ...), then the sequence of convergents {fi(z)} converges uniformly when
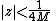
and f(z) is analytic on that open disk.
and later Pringsheim
showed that a continued fraction, in which the as and bs may be complex numbers, will converge to a finite value if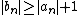
for 
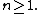
. Suppose that all the ai are equal to 1, and all the bi have arguments
with:
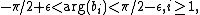
with epsilon being any positive number less than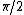
. In other words, all the bi are inside a wedge which has its vertex at the origin, has an opening angle of 
, and is symmetric around the positive real axis. Then fi, the ith convergent to the continued fraction, is finite and has an argument:
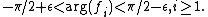
Also, the sequence of even convergents will converge, as will the sequence of odd convergents. The continued fraction itself will converge if and only if the sum of all the |bi| diverges.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
of continued fractions
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
, the convergence problem is the determination of conditions on the partial numerators ai and partial denominators bi that are sufficient to guarantee the convergence of the continued fraction
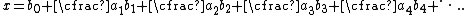
This convergence problem for continued fractions is inherently more difficult (and also more interesting) than the corresponding convergence problem for infinite series.
Elementary results
When the elements of an infinite continued fraction consist entirely of positive real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the determinant formula
Fundamental recurrence formulas
In the theory of continued fractions, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents...
can easily be applied to demonstrate when the continued fraction converges. Since the denominators Bn cannot be zero in this simple case, the problem boils down to showing that the product of successive denominators BnBn+1 grows more quickly than the product of the partial numerators a1a2a3...an+1. The convergence problem is much more difficult when the elements of the continued fraction are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Periodic continued fractions
An infinite periodic continued fraction is a continued fraction of the form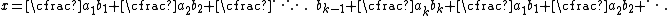where k ≥ 1, the sequence of partial numerators {a1, a2, a3, ..., ak} contains no values equal to zero, and the partial numerators {a1, a2, a3, ..., ak} and partial denominators {b1, b2, b3, ..., bk} repeat over and over again, ad infinitum.
By applying the theory of linear fractional transformations to
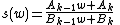
where Ak-1, Bk-1, Ak, and Bk are the numerators and denominators of the k-1st and kth convergents of the infinite periodic continued fraction x, it can be shown that x converges to one of the fixed points of s(w) if it converges at all. Specifically, let r1 and r2 be the roots of the quadratic equation
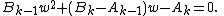
These roots are the fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of s(w). If r1 and r2 are finite then the infinite periodic continued fraction x converges if and only if
- the two roots are equal; or
- the k-1st convergent is closer to r1 than it is to r2, and none of the first k convergents equal r2.
If the denominator Bk-1 is equal to zero then an infinite number of the denominators Bnk-1 also vanish, and the continued fraction does not converge to a finite value. And when the two roots r1 and r2 are equidistant from the k-1st convergent – or when r1 is closer to the k-1st convergent than r2 is, but one of the first k convergents equals r2 – the continued fraction x diverges by oscillation.
The special case when period k = 1
If the period of a continued fraction is 1; that is, ifwhere b ≠ 0, we can obtain a very strong result. First, by applying an equivalence transformation we see that x converges if and only if
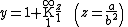
converges. Then, by applying the more general result obtained above it can be shown that
converges for every complex number z except when z is a negative real number and z < −¼. Moreover, this continued fraction y converges to the particular value of
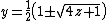
that has the larger absolute value (except when z is real and z < −¼, in which case the two fixed points of the LFT generating y have equal moduli and y diverges by oscillation).
By applying another equivalence transformation the condition that guarantees convergence of
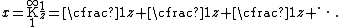
can also be determined. Since a simple equivalence transformation shows that
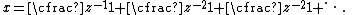
whenever z ≠ 0, the preceding result for the continued fraction y can be restated for x. The infinite periodic continued fraction
converges if and only if z2 is not a real number lying in the interval −4 < z2 ≤ 0 – or, equivalently, x converges if and only if z ≠ 0 and z is not a pure imaginary number lying in the interval −2i < z < 2i.
Worpitzky's theorem
By applying the fundamental inequalities to the continued fraction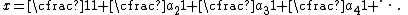it can be shown that the following statements hold if |ai| ≤ ¼ for the partial numerators ai, i = 2, 3, 4, ...
- The continued fraction x converges to a finite value, and converges uniformly if the partial numerators ai are complex variables.
- The value of x and of each of its convergents xi lies in the circular domain of radius 2/3 centered on the point z = 4/3; that is, in the region defined by
-
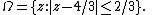
- The radius ¼ is the largest radius over which x can be shown to converge without exception, and the region Ω is the smallest image space that contains all possible values of the continued fraction x.
The proof of the first statement, by Julius Worpitzky in 1865, is apparently the oldest published proof that a continued fraction with complex elements actually converges.
Because the proof of Worpitzky's theorem employs Euler's continued fraction formula to construct an infinite series that is equivalent to the continued fraction x, and the series so constructed is absolutely convergent, the Weierstrass M-test can be applied to a modified version of x. If
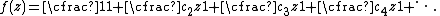
and a positive real number M exists such that |ci| ≤ M (i = 2, 3, 4, ...), then the sequence of convergents {fi(z)} converges uniformly when
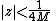
and f(z) is analytic on that open disk.
Śleszyński–Pringsheim criterion
In the late 19-th century, ŚleszyńskiIvan Sleszynski
Ivan Śleszyński was a Ukrainian-born Polish mathematician. Śleszyński's main work was on continued fractions, least squares and axiomatic proof theory based on mathematical logic. He and Alfred Pringsheim, working separately, proved what is now called the Śleszyński–Pringsheim theorem.-External...
and later Pringsheim
Alfred Pringsheim
Alfred Israel Pringsheim was a German mathematician and patron of the arts. He was born in Ohlau, Prussian Silesia and died in Zürich, Switzerland.- Family and academic career :...
showed that a continued fraction, in which the as and bs may be complex numbers, will converge to a finite value if
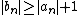for 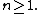Van Vleck's theorem
Jones and Thron attribute the following result to Van VleckEdward Burr Van Vleck
Edward Burr Van Vleck was an American mathematician.The son of astronomer John Monroe Van Vleck, he graduated from Wesleyan University in 1884, attended Johns Hopkins in 1885-87, and studied at Göttingen...
. Suppose that all the ai are equal to 1, and all the bi have arguments
Arg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
with:
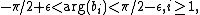
with epsilon being any positive number less than
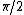. In other words, all the bi are inside a wedge which has its vertex at the origin, has an opening angle of , and is symmetric around the positive real axis. Then fi, the ith convergent to the continued fraction, is finite and has an argument: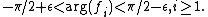Also, the sequence of even convergents will converge, as will the sequence of odd convergents. The continued fraction itself will converge if and only if the sum of all the |bi| diverges.