
Tower of fields
Encyclopedia
In mathematics
, a tower of fields is a sequence of field extension
s
The name refers to the fact that such sequences are often written as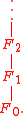
A tower of fields is called infinite if it is an infinite sequence, otherwise it is called finite.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a tower of fields is a sequence of field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s
The name refers to the fact that such sequences are often written as
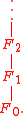
A tower of fields is called infinite if it is an infinite sequence, otherwise it is called finite.
Examples
is a finite tower with rational, real and complex numbers.- The sequence obtained by letting F0 be the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q, and letting
-
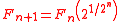 |adjoining]] a 2nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
|adjoining]] a 2nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
of 2) is an infinite tower.- If p is a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
the pth cyclotomic tower of Q is obtained by letting F0 = Q and Fn be the field obtained by adjoining to Q the pnth roots of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. This tower is of fundamental importance in Iwasawa theoryIwasawa theoryIn number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
. - The Golod–Shafarevich theoremGolod–Shafarevich theoremIn mathematics, the Golod–Shafarevich theorem was proved in 1964 by two Russian mathematicians, Evgeny Golod and Igor Shafarevich. It is a result in non-commutative homological algebra which has consequences in various branches of algebra.-The inequality:...
shows that there are infinite towers obtained by iterating the Hilbert class fieldHilbert class fieldIn algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
construction to a number field.
- If p is a prime number

