Algebraic geometry of projective spaces
Encyclopedia
Projective space
s play a central role in algebraic geometry
. The aim of this article is to define the notion in terms of abstract algebraic geometry
and to describe some basic uses of those spaces.
, and V be a finite dimensional vector space
over k. The symmetric algebra
of the dual vector space V* is called the polynomial ring
on V and denoted by k[V]. It is a naturally graded algebra
by the degree of polynomials.
The projective Nullstellensatz states that, for any homogeneous ideal I that does not contain all polynomials over a certain degree, the common zero locus of all polynomials in I (or Nullstelle) is not reduced to {0}, and, more precisely, the ideal of polynomials that vanish on that locus coincide with the radical
of the ideal I.
This last assertion is best summarized by the formula : for any relevant ideal I,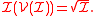
In particular, maximal homogeneous relevant ideals of k[V] correspond biunivocally to lines through the origin of V.
over a field
k. The scheme
over k defined by Proj(k[V]) is called projectivization of V. The projective n-space on k is the projectivization of the vector space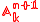
.
The definition of the sheaf is done on the base of open sets
of principal open sets D(P), where P runs along the set of homogeneous polynomials, by setting the sections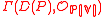
to be the ring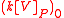
, the zero degree component of the ring obtained by localization
at P. Its elements are therefore the rational fractions with homogeneous numerator and some power of P as the denominator, with same degree as the numerator.
The situation is most clear at a non-vanishing linear form φ. The restriction of the structure sheaf to the open set D(φ) is then canonically identified with the affine scheme spec(k[ker φ]). Since the D(φ) form an open cover of X the projective schemes can be thought of as being obtained by the gluing via projectivization of isomorphic affine schemes.
It can be noted that the ring of global sections of this scheme is a field, which implies that the scheme is not affine. Any two open sets intersect non-trivially: ie the scheme is irreducible
. When the field k is algebraically closed,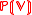
is in fact an abstract variety
, that furthermore is complete. cf. Glossary of scheme theory
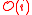, the Serre twisting sheaves. All of these sheaves are in fact line bundle
s. By the correspondence between Cartier divisors and line bundles, the first twisting sheaf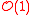
is equivalent to hyperplane divisors.
Since the ring of polynomials is a unique factorization domain
, any prime ideal
of height 1 is principal
, which shows that any Weil divisor is linearly equivalent to some power of a hyperplane divisor. This consideration proves that the Picard group of a projective space is free of rank 1. That is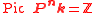
, and the isomorphism is given by the degree of divisors.
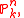for k a field
, are exactly the twisting sheaves
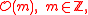so the Picard group of 
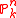is isomorphic to 
. The isomorphism is given by the first Chern class.
The space of local sections on an open set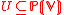
of the line bundle 
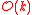is the space of homogeneous degree k regular functions on the cone in V associated to U. In particular, the space of global sections
vanishes if m < 0, and consists of constants in k for m=0 and of homogeneous polynomials of degree m for m > 0.
The Birkhoff-Grothendieck theorem states that on the projective line, any vector bundle splits in a unique way as a direct sum of the line bundles.
, which appears for instance as the exceptional divisor
of the blowing up
of a smooth point
is the sheaf
. The canonical bundle
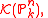is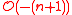 
.
This fact derives from a fundamental geometric statement on projective spaces: the Euler exact sequence.
The negativity of the canonical line bundle makes projective spaces prime examples of Fano varieties
, equivalently, their anticanonical line bundle is ample (in fact very ample). Their index (cf. Fano varieties
) is given by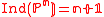
, and, by a theorem of Kobayashi-Ochiai, projective spaces are characterized amongst Fano varieties by the property
.
Any choice of a finite system of non simultaneously vanishing global sections of a globally generated line bundle
defines a morphism (algebraic geometry) to a projective space. A line bundle whose base can be embedded in a projective space by such a morphism is called very ample.
The group of symmetries of the projective space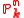
is the group of projectivized linear automorphisms 
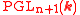. The choice of a morphism to a projective space 
modulo the action of this group is in fact equivalent to the choice of a globally generating n-dimensional linear system
on a line bundle
on X. The choice of a projective embedding of X, modulo projective transformations is likewise equivalent to the choice of a very ample line bundle on X.
A morphism to a projective space
defines a globally generated line bundle by 
and a linear system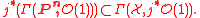
If the range of the morphism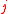
is not contained in a hyperplane divisor, then the pull-back is an injection and the linear system of divisors
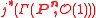is a linear system of dimension n.
for 
See the answer on MathOverflow for an application of the Veronese embedding to the calculation of cohomology groups of smooth projective hypersurface
s (smooth divisors).
. The intersection theory of curves in the projective plane yields the Bezout theorem.
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s play a central role in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The aim of this article is to define the notion in terms of abstract algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and to describe some basic uses of those spaces.
Homogeneous polynomial ideals
Let k be an algebraically closed fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, and V be a finite dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over k. The symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
of the dual vector space V* is called the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
on V and denoted by k[V]. It is a naturally graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
by the degree of polynomials.
The projective Nullstellensatz states that, for any homogeneous ideal I that does not contain all polynomials over a certain degree, the common zero locus of all polynomials in I (or Nullstelle) is not reduced to {0}, and, more precisely, the ideal of polynomials that vanish on that locus coincide with the radical
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of the ideal I.
This last assertion is best summarized by the formula : for any relevant ideal I,
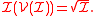
In particular, maximal homogeneous relevant ideals of k[V] correspond biunivocally to lines through the origin of V.
Construction of projectivized schemes
Let V be a finite dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k. The scheme
Scheme
Scheme may refer to:* Scheme , a minimalist, multi-paradigm dialect of Lisp* Scheme , a concept in algebraic geometry* Scheme , a figure of speech that changes a sentence's structure-See also:...
over k defined by Proj(k[V]) is called projectivization of V. The projective n-space on k is the projectivization of the vector space
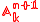.The definition of the sheaf is done on the base of open sets
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
of principal open sets D(P), where P runs along the set of homogeneous polynomials, by setting the sections
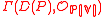
to be the ring
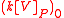, the zero degree component of the ring obtained by localizationLocalization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
at P. Its elements are therefore the rational fractions with homogeneous numerator and some power of P as the denominator, with same degree as the numerator.
The situation is most clear at a non-vanishing linear form φ. The restriction of the structure sheaf to the open set D(φ) is then canonically identified with the affine scheme spec(k[ker φ]). Since the D(φ) form an open cover of X the projective schemes can be thought of as being obtained by the gluing via projectivization of isomorphic affine schemes.
It can be noted that the ring of global sections of this scheme is a field, which implies that the scheme is not affine. Any two open sets intersect non-trivially: ie the scheme is irreducible
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
. When the field k is algebraically closed,
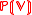is in fact an abstract varietyAbstract variety
In mathematics, in the field of algebraic geometry, the idea of abstract variety is to define a concept of algebraic variety in an intrinsic way. This followed the trend in the definition of manifold independent of any ambient space by some years, the first notions being those of Oscar Zariski and...
, that furthermore is complete. cf. Glossary of scheme theory
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
Divisors and twisting sheaves
The Proj functor in fact gives more than a mere scheme: a sheaf in graded modules over the structure sheaf is defined in the process. The homogeneous components of this graded sheaf are denoted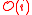, the Serre twisting sheaves. All of these sheaves are in fact line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s. By the correspondence between Cartier divisors and line bundles, the first twisting sheaf
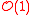is equivalent to hyperplane divisors.Since the ring of polynomials is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, any prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of height 1 is principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, which shows that any Weil divisor is linearly equivalent to some power of a hyperplane divisor. This consideration proves that the Picard group of a projective space is free of rank 1. That is
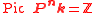, and the isomorphism is given by the degree of divisors.Classification of vector bundles
The invertible sheaves, or line bundles, on the projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
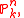for k a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, are exactly the twisting sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
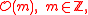so the Picard group of 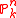is isomorphic to . The isomorphism is given by the first Chern class.The space of local sections on an open set
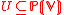of the line bundle 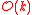is the space of homogeneous degree k regular functions on the cone in V associated to U. In particular, the space of global sectionsvanishes if m < 0, and consists of constants in k for m=0 and of homogeneous polynomials of degree m for m > 0.
The Birkhoff-Grothendieck theorem states that on the projective line, any vector bundle splits in a unique way as a direct sum of the line bundles.
Important line bundles
The tautological bundleTautological bundle
In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
, which appears for instance as the exceptional divisor
Exceptional divisor
In mathematics, specifically algebraic geometry, an exceptional divisor for a regular mapf: X \rightarrow Yof varieties is a kind of 'large' subvariety of X which is 'crushed' by f, in a certain definite sense...
of the blowing up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
of a smooth point
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
is the sheaf
. The canonical bundleCanonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
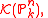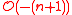is .This fact derives from a fundamental geometric statement on projective spaces: the Euler exact sequence.
The negativity of the canonical line bundle makes projective spaces prime examples of Fano varieties
Fano variety
In algebraic geometry, a Fano variety, introduced by , is a non-singular complete variety whose anticanonical bundle is ample.Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces....
, equivalently, their anticanonical line bundle is ample (in fact very ample). Their index (cf. Fano varieties
Fano variety
In algebraic geometry, a Fano variety, introduced by , is a non-singular complete variety whose anticanonical bundle is ample.Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces....
) is given by
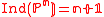, and, by a theorem of Kobayashi-Ochiai, projective spaces are characterized amongst Fano varieties by the property.Morphisms to projective schemes
As affine spaces can be embedded in projective spaces, all affine varieties can be embedded in projective spaces too.Any choice of a finite system of non simultaneously vanishing global sections of a globally generated line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
defines a morphism (algebraic geometry) to a projective space. A line bundle whose base can be embedded in a projective space by such a morphism is called very ample.
The group of symmetries of the projective space
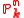is the group of projectivized linear automorphisms 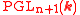. The choice of a morphism to a projective space modulo the action of this group is in fact equivalent to the choice of a globally generating n-dimensional linear systemLinear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
on a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
on X. The choice of a projective embedding of X, modulo projective transformations is likewise equivalent to the choice of a very ample line bundle on X.
A morphism to a projective space
defines a globally generated line bundle by and a linear system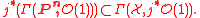If the range of the morphism
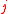is not contained in a hyperplane divisor, then the pull-back is an injection and the linear system of divisorsLinear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
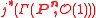is a linear system of dimension n.An example: the Veronese embeddings
The Veronese embeddings are embeddings for See the answer on MathOverflow for an application of the Veronese embedding to the calculation of cohomology groups of smooth projective hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s (smooth divisors).
Curves in projective spaces
As Fano varieties, the projective spaces are ruled varietiesRuled variety
In mathematics, a ruled variety is a variety birational to a product of the projective line and another variety, and a uniruled variety is a variety that is dominated by a ruled variety...
. The intersection theory of curves in the projective plane yields the Bezout theorem.
General algebraic geometry
- Scheme (mathematics)Scheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
- Projective variety
- Proj constructionProj constructionIn algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...
General projective geometry
- Projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
- Projective geometryProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
- Homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...