Stokes drift - AbsoluteAstronomy.com

For a pure wave

Wave

In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...

motion

Motion (physics)

In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...

in fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

, the Stokes drift velocity is the average

Average

In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....

velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

when following a specific fluid

Fluid

In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....

parcel as it travels with the fluid flow. For instance, a particle floating at the free surface

Free surface

In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...

of water waves, experiences a net Stokes drift velocity in the direction of wave propagation

Wave propagation

Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....

.

More generally, the Stokes drift velocity is the difference between the average

Average

Lagrangian

Lagrangian and Eulerian coordinates

In fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...

flow velocity

Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...

of a fluid parcel, and the average Eulerian

Lagrangian and Eulerian coordinates

flow velocity

Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...

of the fluid

Fluid

at a fixed position. This nonlinear phenomenon is named after George Gabriel Stokes

George Gabriel Stokes

Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...

, who derived expressions for this drift in his 1847 study of water waves.

The Stokes drift is the difference in end positions, after a predefined amount of time (usually one wave period), as derived from a description in the Lagrangian and Eulerian coordinates

Lagrangian and Eulerian coordinates

. The end position in the Lagrangian description

Lagrangian and Eulerian coordinates

is obtained by following a specific fluid parcel during the time interval. The corresponding end position in the Eulerian description

Lagrangian and Eulerian coordinates

is obtained by integrating the flow velocity

Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...

at a fixed position—equal to the initial position in the Lagrangian description—during the same time interval.

The Stokes drift velocity equals the Stokes drift divided by the considered time interval.
Often, the Stokes drift velocity is loosely referred to as Stokes drift.
Stokes drift may occur in all instances of oscillatory flow which are inhomogeneous in space. For instance in water waves, tide

Tide

Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....

s and atmospheric waves.

In the Lagrangian description

Lagrangian and Eulerian coordinates

, fluid parcels may drift far from their initial positions. As a result, the unambiguous definition of an average

Average

Lagrangian velocity and Stokes drift velocity, which can be attributed to a certain fixed position, is by no means a trivial task. However, such an unambiguous description is provided by the Generalized Lagrangian Mean (GLM) theory of Andrews and McIntyre in 1978.

The Stokes drift is important for the mass transfer

Mass transfer

Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...

of all kind of materials and organisms by oscillatory flows. Further the Stokes drift is important for the generation of Langmuir circulation

Langmuir circulation

Langmuir circulation is a wind driven helix circulation in the ocean with the axis almost parallel to the wind. Irving Langmuir discovered this phenomenon after noticing windrows of seaweed in the Sargasso Sea in 1938....

s.
For nonlinear and periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

water waves, accurate results on the Stokes drift have been computed and tabulated.

Mathematical description

The Lagrangian motion

Lagrangian and Eulerian coordinates

of a fluid parcel with position vector x = ξ(α,t) in the Eulerian coordinates is given by:

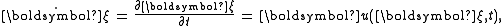
where ∂ξ / ∂t is the partial derivative

Partial derivative

In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...

of ξ(α,t) with respect to t, and

ξ(α,t) is the Lagrangian position vector of a fluid parcel, in meters,

u(x,t) is the Eulerian velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

, in meters per second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

,

x is the position vector in the Eulerian coordinate system
Lagrangian and Eulerian coordinates
In fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...

, in meters,

α is the position vector in the Lagrangian coordinate system
Lagrangian and Eulerian coordinates
In fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...

, in meters,

t is the time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

, in seconds
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

.

Often, the Lagrangian coordinates α are chosen to coincide with the Eulerian coordinates x at the initial time t = t₀ :
But also other ways of label
Label
A label is a piece of paper, polymer, cloth, metal, or other material affixed to a container or article, on which is printed a legend, information concerning the product, addresses, etc. A label may also be printed directly on the container or article....

ing the fluid parcels are possible.

If the average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....

value of a quantity is denoted by an overbar, then the average Eulerian velocity vector ū_E and average Lagrangian velocity vector ū_L are:

Different definitions of the average

Average

may be used, depending on the subject of study, see ergodic theory:

time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

average,
space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...

average,
ensemble average
Ensemble average
In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....

and
phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

average.

Now, the Stokes drift velocity ū_S equals

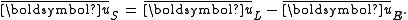
In many situations, the mapping

Map (mathematics)

In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...

of average quantities from some Eulerian position x to a corresponding Lagrangian position α forms a problem. Since a fluid parcel with label α traverses along a path

Path (topology)

In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...

of many different Eulerian positions x, it is not possible to assign α to a unique x.
A mathematical sound basis for an unambiguous mapping between average Lagrangian and Eulerian quantities is provided by the theory of the Generalized Lagrangian Mean (GLM) by Andrews and McIntyre (1978).

Example: Deep water waves

The Stokes drift was formulated for water waves by George Gabriel Stokes

George Gabriel Stokes

Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...

in 1847. For simplicity, the case of infinite-deep water is considered, with linear

Linear

In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...

wave propagation

Wave propagation

of a sinusoidal wave on the free surface

Free surface

of a fluid layer:

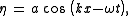
where

η is the elevation

Elevation

The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....

of the free surface

Free surface

in the z-direction (meters),

a is the wave amplitude

Amplitude

Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...

(meters),

k is the wave number: k = 2π / λ (radians

Radian

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...

per meter),

ω is the angular frequency

Angular frequency

In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...

: ω = 2π / T (radians

Radian

per second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

x is the horizontal coordinate and the wave propagation direction (meters),

z is the vertical coordinate, with the positive z direction pointing out of the fluid layer (meters),

λ is the wave length (meters), and

T is the wave period (seconds

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

It is assumed that the waves are of infinitesimal

Infinitesimal

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

amplitude

Amplitude

and the free surface

Free surface

oscillates around the mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

level z = 0. The waves propagate under the action of gravity, with a constant acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

vector by gravity (pointing downward in the negative z-direction). Further the fluid is assumed to be inviscid and incompressible, with a constant mass density. The fluid flow

Flow (mathematics)

In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...

is irrotational. At infinite depth, the fluid is taken to be at rest

Rest (physics)

Rest in physics refers to an object being stationary relative to a particular frame of reference or another object. According to the theory of relativity it is said that an object is: at rest relative to another. For example, a train decelerates on approach to a station and eventually stops...

.

Now the flow

Flow (mathematics)

may be represented by a velocity potential φ, satisfying the Laplace equation and

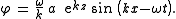
In order to have non-trivial solutions for this eigenvalue problem, the wave length and wave period may not be chosen arbitrarily, but must satisfy the deep-water dispersion

Dispersion (water waves)

In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...

relation:

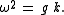
with g the acceleration

Acceleration

by gravity in (m / s²). Within the framework of linear

Linear

In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...

theory, the horizontal and vertical components, ξ_x and ξ_z respectively, of the Lagrangian position ξ are:

The horizontal component ū_S of the Stokes drift velocity is estimated by using a Taylor expansion around x of the Eulerian horizontal-velocity component u_x = ∂ξ_x / ∂t at the position ξ :

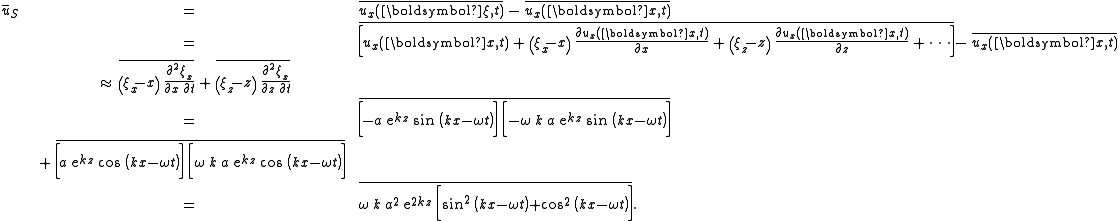
Performing the averaging, the horizontal component of the Stokes drift velocity for deep-water waves is approximately:

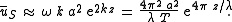
As can be seen, the Stokes drift velocity ū_S is a nonlinear quantity in terms of the wave amplitude

Amplitude

a. Further, the Stokes drift velocity decays exponentially with depth: at a depth of a quart wavelength, z = -¼ λ, it is about 4% of its value at the mean free surface

Free surface

, z = 0.

Mathematical description

Example: Deep water waves

See also

Historical

Other