
Square number
Encyclopedia
In mathematics
, a square number, sometimes also called a perfect square, is an integer
that is the square of an integer; in other words, it is the product of some integer with itself. So, for example, 9 is a square number, since it can be written as 3 × 3.
The usual notation for the formula for the square of a number n is not the product n × n, but the equivalent exponentiation
n2, usually pronounced as "n squared". The name square number comes from the name of the shape. This is because a square with side length n has area
n2.
Square numbers are non-negative. Another way of saying that a (non-negative) number is a square number, is that its square root
is again an integer. For example, √9 = 3, so 9 is a square number.
A positive integer that has no perfect square divisor
s except 1 is called square-free
.
For a non-negative integer n, the nth square number is n2, with 02 = 0 being the zeroth
square. The concept of square can be extended to some other number systems. If rational numbers are included, then a square is the ratio of two square integers, and, conversely, the ratio of two square integers is a square (e.g., 4/9 = (2/3)2).
Starting with 1, there are square numbers up to and including m, where the expression
square numbers up to and including m, where the expression  represents the floor
represents the floor
of the number x.
The difference between any perfect square and its predecessor is given by the identity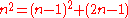 . Equivalently, it is possible to count up square numbers by adding together the last square, the last square's root, and the current root, that is,
. Equivalently, it is possible to count up square numbers by adding together the last square, the last square's root, and the current root, that is, 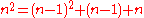 .
.
The expression for the nth square number is n2. This is also equal to the sum of the first n odd numbers as can be seen in the above pictures, where a square results from the previous one by adding an odd number of points (shown in magenta). The formula follows: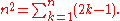
So for example, 52 = 25 = 1 + 3 + 5 + 7 + 9.
There are several recursive
methods for computing square numbers. For example, the nth square number can be computed from the previous square by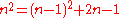 . Alternatively, the nth square number can be calculated from the previous two by doubling the (n − 1)-th square, subtracting the (n − 2)-th square number, and adding 2, because n2 = 2(n − 1)2 − (n − 2)2 + 2. For example, 2 × 52 − 42 + 2 = 2 × 25 − 16 + 2 = 50 − 16 + 2 = 36 = 62.
. Alternatively, the nth square number can be calculated from the previous two by doubling the (n − 1)-th square, subtracting the (n − 2)-th square number, and adding 2, because n2 = 2(n − 1)2 − (n − 2)2 + 2. For example, 2 × 52 − 42 + 2 = 2 × 25 − 16 + 2 = 50 − 16 + 2 = 36 = 62.
A square number is also the sum of two consecutive triangular number
s. The sum of two consecutive square numbers is a centered square number
. Every odd square is also a centered octagonal number
.
Another property of a square number is that it has an odd number of divisors, while other numbers have an even number of divisors. An integer root is the only divisor that pairs up with itself to yield the square number, while other divisors come in pairs.
Lagrange's four-square theorem
states that any positive integer can be written as the sum of four or fewer perfect squares. Three squares are not sufficient for numbers of the form 4k(8m + 7). A positive integer can be represented as a sum of two squares precisely if its prime factorization contains no odd powers of primes of the form 4k + 3. This is generalized by Waring's problem
.
A square number can end only with digits 0,1,4,6,9, or 25 in base 10, as follows:
In base 16, a square number can end only with 0,1,4 or 9 and
- in case 0, only 0,1,4,9 can precede it,
- in case 4, only even numbers can precede it.
In general, if a prime
p divides a square number m then the square of p must also divide m; if p fails to divide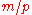 , then m is definitely not square. Repeating the divisions of the previous sentence, one concludes that every prime must divide a given perfect square an even number of times (including possibly 0 times). Thus, the number m is a square number if and only if, in its canonical representation, all exponents are even.
, then m is definitely not square. Repeating the divisions of the previous sentence, one concludes that every prime must divide a given perfect square an even number of times (including possibly 0 times). Thus, the number m is a square number if and only if, in its canonical representation, all exponents are even.
Squarity testing can be used as alternative way in factorization
of large numbers. Instead of testing for divisibility, test for squarity: for given m and some number k, if k² − m is the square of an integer n then k − n divides m. (This is an application of the factorization of a difference of two squares
.) For example, 100² − 9991 is the square of 3, so consequently 100 − 3 divides 9991. This test is deterministic for odd divisors in the range from k − n to k + n where k covers some range of natural numbers k ≥ √m.
A square number cannot be a perfect number
.
The sum of the series of power numbers
can also be represented by the formula
The first terms of this series (the square pyramidal number
s) are:
All fourth powers, sixth powers, eighth powers and so on are perfect squares.
Squares of odd numbers are odd, since (2n + 1)2 = 4(n2 + n) + 1.
It follows that square roots of even square numbers are even, and square roots of odd square numbers are odd.
negative numbers is positive, and the product of two real positive numbers is also positive, it follows that no square number is negative. It follows that no square root
can be taken of a negative number within the system of real number
s. This leaves a gap in the real number system that mathematicians fill by postulating complex number
s, beginning with the imaginary unit
i, which by convention is one of the square roots of −1.
Squaring is used in statistics
in determining the standard deviation
of a set of values. The deviation of each value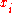 from the mean
from the mean
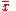 of the set is defined as the difference
of the set is defined as the difference 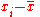 . These deviations are squared, then a mean is taken of the new set of numbers (each of which is positive). This mean is the variance
. These deviations are squared, then a mean is taken of the new set of numbers (each of which is positive). This mean is the variance
, and its square root is the standard deviation. In finance
, the volatility
of a financial instrument is the standard deviation of its values.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a square number, sometimes also called a perfect square, is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
that is the square of an integer; in other words, it is the product of some integer with itself. So, for example, 9 is a square number, since it can be written as 3 × 3.
The usual notation for the formula for the square of a number n is not the product n × n, but the equivalent exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
n2, usually pronounced as "n squared". The name square number comes from the name of the shape. This is because a square with side length n has area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
n2.
Square numbers are non-negative. Another way of saying that a (non-negative) number is a square number, is that its square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
is again an integer. For example, √9 = 3, so 9 is a square number.
A positive integer that has no perfect square divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s except 1 is called square-free
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
.
For a non-negative integer n, the nth square number is n2, with 02 = 0 being the zeroth
Zeroth
Zero-based numbering is numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday circumstances. Under zero-based numbering, the initial element is sometimes termed the zeroth element, rather than the first element; zeroth is a...
square. The concept of square can be extended to some other number systems. If rational numbers are included, then a square is the ratio of two square integers, and, conversely, the ratio of two square integers is a square (e.g., 4/9 = (2/3)2).
Starting with 1, there are
 square numbers up to and including m, where the expression
square numbers up to and including m, where the expression  represents the floor
represents the floorFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
of the number x.
Examples
The squares below 602 are:The difference between any perfect square and its predecessor is given by the identity
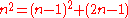 . Equivalently, it is possible to count up square numbers by adding together the last square, the last square's root, and the current root, that is,
. Equivalently, it is possible to count up square numbers by adding together the last square, the last square's root, and the current root, that is, 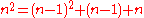 .
.Properties
The number m is a square number if and only if one can arrange m points in a square:| m = 12 = 1 |  |
| m = 22 = 4 |  |
| m = 32 = 9 |  |
| m = 42 = 16 |  |
| m = 52 = 25 |  |
The expression for the nth square number is n2. This is also equal to the sum of the first n odd numbers as can be seen in the above pictures, where a square results from the previous one by adding an odd number of points (shown in magenta). The formula follows:
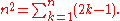
So for example, 52 = 25 = 1 + 3 + 5 + 7 + 9.
There are several recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
methods for computing square numbers. For example, the nth square number can be computed from the previous square by
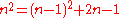 . Alternatively, the nth square number can be calculated from the previous two by doubling the (n − 1)-th square, subtracting the (n − 2)-th square number, and adding 2, because n2 = 2(n − 1)2 − (n − 2)2 + 2. For example, 2 × 52 − 42 + 2 = 2 × 25 − 16 + 2 = 50 − 16 + 2 = 36 = 62.
. Alternatively, the nth square number can be calculated from the previous two by doubling the (n − 1)-th square, subtracting the (n − 2)-th square number, and adding 2, because n2 = 2(n − 1)2 − (n − 2)2 + 2. For example, 2 × 52 − 42 + 2 = 2 × 25 − 16 + 2 = 50 − 16 + 2 = 36 = 62.A square number is also the sum of two consecutive triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s. The sum of two consecutive square numbers is a centered square number
Centered square number
In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each centered square number equals the number of dots within a...
. Every odd square is also a centered octagonal number
Centered octagonal number
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers...
.
Another property of a square number is that it has an odd number of divisors, while other numbers have an even number of divisors. An integer root is the only divisor that pairs up with itself to yield the square number, while other divisors come in pairs.
Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
states that any positive integer can be written as the sum of four or fewer perfect squares. Three squares are not sufficient for numbers of the form 4k(8m + 7). A positive integer can be represented as a sum of two squares precisely if its prime factorization contains no odd powers of primes of the form 4k + 3. This is generalized by Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
.
A square number can end only with digits 0,1,4,6,9, or 25 in base 10, as follows:
- If the last digit of a number is 0, its square ends in an even number of 0s (so at least 00) and the digitsNumerical digitA digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
digits preceding the ending 0s must also form a square. - If the last digit of a number is 1 or 9, its square ends in 1 and the number formed by its preceding digits must be divisible by four.
- If the last digit of a number is 2 or 8, its square ends in 4 and the preceding digit must be even.
- If the last digit of a number is 3 or 7, its square ends in 9 and the number formed by its preceding digits must be divisible by four.
- If the last digit of a number is 4 or 6, its square ends in 6 and the preceding digit must be odd.
- If the last digit of a number is 5, its square ends in 25 and the preceding digits must be 0, 2, 06, or 56.
In base 16, a square number can end only with 0,1,4 or 9 and
- in case 0, only 0,1,4,9 can precede it,
- in case 4, only even numbers can precede it.
In general, if a prime
Prime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
p divides a square number m then the square of p must also divide m; if p fails to divide
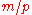 , then m is definitely not square. Repeating the divisions of the previous sentence, one concludes that every prime must divide a given perfect square an even number of times (including possibly 0 times). Thus, the number m is a square number if and only if, in its canonical representation, all exponents are even.
, then m is definitely not square. Repeating the divisions of the previous sentence, one concludes that every prime must divide a given perfect square an even number of times (including possibly 0 times). Thus, the number m is a square number if and only if, in its canonical representation, all exponents are even.Squarity testing can be used as alternative way in factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
of large numbers. Instead of testing for divisibility, test for squarity: for given m and some number k, if k² − m is the square of an integer n then k − n divides m. (This is an application of the factorization of a difference of two squares
Difference of two squares
In mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number...
.) For example, 100² − 9991 is the square of 3, so consequently 100 − 3 divides 9991. This test is deterministic for odd divisors in the range from k − n to k + n where k covers some range of natural numbers k ≥ √m.
A square number cannot be a perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
.
The sum of the series of power numbers
can also be represented by the formula
The first terms of this series (the square pyramidal number
Square pyramidal number
In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square base...
s) are:
0, 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201... .
All fourth powers, sixth powers, eighth powers and so on are perfect squares.
Special cases
- If the number is of the form m5 where m represents the preceding digits, its square is n25 where n = m × (m + 1) and represents digits before 25. For example the square of 65 can be calculated by n = 6 × (6 + 1) = 42 which makes the square equal to 4225.
- If the number is of the form m0 where m represents the preceding digits, its square is n00 where n = m2. For example the square of 70 is 4900.
- If the number has two digits and is of the form 5m where m represents the units digit, its square is AABB where AA = 25 + m and BB = m2. Example: To calculate the square of 57, 25 + 7 = 32 and 72 = 49, which means 572 = 3249.
Odd and even square numbers
Squares of even numbers are even (and in fact divisible by 4), since (2n)2 = 4n2.Squares of odd numbers are odd, since (2n + 1)2 = 4(n2 + n) + 1.
It follows that square roots of even square numbers are even, and square roots of odd square numbers are odd.
Uses
Since the product of realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
negative numbers is positive, and the product of two real positive numbers is also positive, it follows that no square number is negative. It follows that no square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
can be taken of a negative number within the system of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. This leaves a gap in the real number system that mathematicians fill by postulating complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, beginning with the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i, which by convention is one of the square roots of −1.
Squaring is used in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
in determining the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a set of values. The deviation of each value
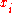 from the mean
from the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
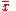 of the set is defined as the difference
of the set is defined as the difference 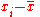 . These deviations are squared, then a mean is taken of the new set of numbers (each of which is positive). This mean is the variance
. These deviations are squared, then a mean is taken of the new set of numbers (each of which is positive). This mean is the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, and its square root is the standard deviation. In finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, the volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of a financial instrument is the standard deviation of its values.
See also
- Square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
- Methods of computing square rootsMethods of computing square rootsThere are several methods for calculating the principal square root of a nonnegative real number. For the square roots of a negative or complex number, see below.- Rough estimation :...
- Quadratic residue
- Polygonal numberPolygonal numberIn mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
- Euler's four-square identityEuler's four-square identityIn mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:=\,...
- Cube (algebra)
- Fermat's theorem on sums of two squares
- Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
- Parallelogram lawParallelogram lawIn mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...
- Brahmagupta–Fibonacci identity
- The Book of SquaresThe Book of SquaresThe Book of Squares, in the original Latin is a book on algebra by Leonardo Fibonacci, published in 1225. Fibonacci's identity, establishing that the set of all sums of two squares is closed under multiplication, appears in it. The book anticipated the works of later mathematicians like Fermat and...
- Integer square rootInteger square rootIn number theory, the integer square root of a positive integer n is the positive integer m which is the greatest integer less than or equal to the square root of n,...
- Square triangular numberSquare triangular numberIn mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
- Automorphic numberAutomorphic numberIn mathematics an automorphic number is a number whose square "ends" in the same digits as number itself. For example, 52 = 25, 762 = 5776, and 8906252 = 793212890625, so 5, 76 and 890625 are all automorphic numbers.The sequence of automorphic numbers begins 1, 5, 6, 25, 76, 376, 625, 9376, .....
- ExponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
- Power of twoPower of twoIn mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
Further reading
- Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-32, 1996. ISBN 0-387-97993-X
External links
- Learn Square Numbers. Practice square numbers up to 144 with this children's multiplication game
- Dario Alpern, Sum of squares. A Java applet to decompose a natural number into a sum of up to four squares.
- Fibonacci and Square Numbers at Convergence
- The first 1,000,000 perfect squares Includes a program for generating perfect squares up to 10^15.



