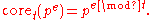Square-free integer
Encyclopedia
In mathematics
, a square-free, or quadratfrei, integer
is one divisible
by no perfect square
, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32. The smallest positive square-free numbers are
Ring theory
generalizes the concept of being square-free
.
occurs more than once. Another way of stating the same is that for every prime factor
p of n, the prime p does not divide n / p. Yet another formulation: n is square-free if and only if in every factorization n = ab, the factors a and b are coprime
. An immediate result of this definition is that all prime numbers are square-free.
The positive integer n is square-free if and only if
μ(n) ≠ 0, where μ denotes the Möbius function
.
The Dirichlet series that generates the square-free numbers is
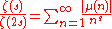where ζ(s) is the Riemann zeta function.
This is easily seen from the Euler product
The positive integer n is square-free if and only if all abelian group
s of order
n are isomorphic
, which is the case if and only if all of them are cyclic
. This follows from the classification of finitely generated abelian group
s.
The integer n is square-free if and only if the factor ring Z / nZ (see modular arithmetic
) is a product
of field
s. This follows from the Chinese remainder theorem
and the fact that a ring of the form Z / kZ is a field if and only if k is a prime.
For every positive integer n, the set of all positive divisors of n becomes a partially ordered set
if we use divisibility
as the order relation. This partially ordered set is always a distributive lattice
. It is a Boolean algebra if and only if n is square-free.
The radical of an integer is always square-free.
This argument can be made rigorous to yield:
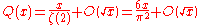
(see pi
and big O notation
). Under the Riemann hypothesis
, the error term can be reduced:
See the race between the number of square-free numbers up to n and round(n/ζ(2)) on the OEIS:
A158819 – (Number of square-free numbers ≤ n) minus round(n/ζ(2)).
The asymptotic/natural density
of square-free numbers is therefore
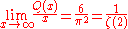
where ζ is the Riemann zeta function and 1/ζ(2) is approximately 0.6079 (nearly 3/5 of the integers are squarefree).
Likewise, if Q(x,n) denotes the number of n-free integers (e.g. 3-free integers being cube-free integers) between 1 and x, one can show
then we may take those
and use them as bits in a binary number, i.e. with the encoding:
e.g. The square-free number 42 has factorisation 2 × 3 × 7, or as an infinite product: 21 · 31 · 50 · 71 · 110 · 130 · ...; Thus the number 42 may be encoded as the binary sequence ...001011 or 11 decimal. (Note that the binary digits are reversed from the ordering in the infinite product.)
Since the prime factorisation of every number is unique, so then is every binary encoding of the square-free integers.
The converse is also true. Since every positive integer has a unique binary representation it is possible to reverse this encoding so that they may be 'decoded' into a unique square-free integer.
Again, for example if we begin with the number 42, this time as simply a positive integer, we have its binary representation 101010. This 'decodes' to become 20 · 31 · 50 · 71 · 110 · 131 = 3 × 7 × 13 = 273.
Among other things, this implies that the set of all square-free integers has the same cardinality as the set of all integers. In turn that leads to the fact that the in-order encodings of the square-free integers are a permutation of the set of all integers.
See sequences A048672 and A064273 in the OEIS
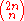
is never squarefree for n > 4. This was proved in 1996 by Olivier Ramaré
and Andrew Granville
.
is defined
to map positive integers n to t-free numbers by reducing the
exponents in the prime power representation modulo t:
The value set of
, in particular, are the
square-free integers. Their Dirichlet generating functions are
OEIS representatives are (t=2), (t=3) and (t=4).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a square-free, or quadratfrei, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is one divisible
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
by no perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32. The smallest positive square-free numbers are
- 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 33, 34, 35, 37, 38, 39, ...
Ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
generalizes the concept of being square-free
Square-free
In mathematics, an element r of a unique factorization domain R is called square-free if it is not divisible by a non-trivial square. That is, every s such that s^2\mid r is a unit of R....
.
Equivalent characterizations
The positive integer n is square-free if and only if in the prime factorization of n, no prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
occurs more than once. Another way of stating the same is that for every prime factor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
p of n, the prime p does not divide n / p. Yet another formulation: n is square-free if and only if in every factorization n = ab, the factors a and b are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. An immediate result of this definition is that all prime numbers are square-free.
The positive integer n is square-free if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
μ(n) ≠ 0, where μ denotes the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
The Dirichlet series that generates the square-free numbers is
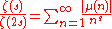where ζ(s) is the Riemann zeta function.This is easily seen from the Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
The positive integer n is square-free if and only if all abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
n are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
, which is the case if and only if all of them are cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. This follows from the classification of finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s.
The integer n is square-free if and only if the factor ring Z / nZ (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
) is a product
Product of rings
In mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
of field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s. This follows from the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
and the fact that a ring of the form Z / kZ is a field if and only if k is a prime.
For every positive integer n, the set of all positive divisors of n becomes a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
if we use divisibility
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
as the order relation. This partially ordered set is always a distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
. It is a Boolean algebra if and only if n is square-free.
The radical of an integer is always square-free.
Distribution
Let Q(x) denote the number of square-free (quadratfrei) integers between 1 and x. For large n, 3/4 of the positive integers less than n are not divisible by 4, 8/9 of these numbers are not divisible by 9, and so on. Because these events are independent, we obtain the approximation:This argument can be made rigorous to yield:
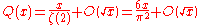
(see pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
and big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). Under the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, the error term can be reduced:
See the race between the number of square-free numbers up to n and round(n/ζ(2)) on the OEIS:
A158819 – (Number of square-free numbers ≤ n) minus round(n/ζ(2)).
The asymptotic/natural density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
of square-free numbers is therefore
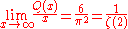
where ζ is the Riemann zeta function and 1/ζ(2) is approximately 0.6079 (nearly 3/5 of the integers are squarefree).
Likewise, if Q(x,n) denotes the number of n-free integers (e.g. 3-free integers being cube-free integers) between 1 and x, one can show
Encoding as binary numbers
If we represent a square-free number as the infinite product:then we may take those
and use them as bits in a binary number, i.e. with the encoding:e.g. The square-free number 42 has factorisation 2 × 3 × 7, or as an infinite product: 21 · 31 · 50 · 71 · 110 · 130 · ...; Thus the number 42 may be encoded as the binary sequence ...001011 or 11 decimal. (Note that the binary digits are reversed from the ordering in the infinite product.)
Since the prime factorisation of every number is unique, so then is every binary encoding of the square-free integers.
The converse is also true. Since every positive integer has a unique binary representation it is possible to reverse this encoding so that they may be 'decoded' into a unique square-free integer.
Again, for example if we begin with the number 42, this time as simply a positive integer, we have its binary representation 101010. This 'decodes' to become 20 · 31 · 50 · 71 · 110 · 131 = 3 × 7 × 13 = 273.
Among other things, this implies that the set of all square-free integers has the same cardinality as the set of all integers. In turn that leads to the fact that the in-order encodings of the square-free integers are a permutation of the set of all integers.
See sequences A048672 and A064273 in the OEIS
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
Erdős squarefree conjecture
The central binomial coefficientCentral binomial coefficient
In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient byThey are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle...
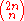
is never squarefree for n > 4. This was proved in 1996 by Olivier Ramaré
Olivier Ramaré
Olivier Ramaré is a French mathematician who teaches at the Université des Sciences et Technologies de Lille.In 1995, he sharpened earlier work on Schnirelmann's theorem by proving that every even number is a sum of at most six primes. This result may be compared with Goldbach's conjecture, which...
and Andrew Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
.
Squarefree core
The multiplicative functionMultiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
is definedto map positive integers n to t-free numbers by reducing the
exponents in the prime power representation modulo t:
The value set of
, in particular, are thesquare-free integers. Their Dirichlet generating functions are
-
.
OEIS representatives are (t=2), (t=3) and (t=4).