
The Book of Squares
Encyclopedia
The Book of Squares, in the original Latin
is a book on algebra
by Leonardo Fibonacci, published in 1225. Fibonacci's identity
, establishing that the set of all sums of two squares is closed under multiplication, appears in it. The book anticipated the works of later mathematicians like Fermat
and Euler
. The book examines several topics in number theory, among them an inductive method for finding Pythagorean triples based on the sequence of odd integers, and on the fact that the sum of the first members of this sequence is
members of this sequence is 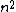 .
.
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
is a book on algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
by Leonardo Fibonacci, published in 1225. Fibonacci's identity
Brahmagupta-Fibonacci identity
In algebra, Brahmagupta's identity, also called Fibonacci's identity, implies that the product of two sums each of two squares is itself a sum of two squares. In other words, the set of all sums of two squares is closed under multiplication...
, establishing that the set of all sums of two squares is closed under multiplication, appears in it. The book anticipated the works of later mathematicians like Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
and Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. The book examines several topics in number theory, among them an inductive method for finding Pythagorean triples based on the sequence of odd integers, and on the fact that the sum of the first
 members of this sequence is
members of this sequence is 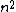 .
.
