Difference of two squares
Encyclopedia
In mathematics
, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number. It refers to the identity
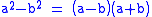
from elementary algebra
.
is straightforward, starting from the RHS
: apply the distributive law to get a sum of four terms, and set as an application of the commutative law. The resulting identity is one of the most commonly used in all of mathematics.
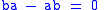
The proof just given indicates the scope of the identity in abstract algebra
: it will hold in any commutative ring
R.
Also, conversely, if this identity holds in a ring
R for all pairs of elements a and b of the ring, then R is commutative. To see this, we apply the distributive law to the right-hand side of the original equation and get
and if this is equal to
, then we have
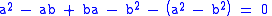
and by associativity
and the rule that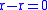
, we can rewrite this as
If the original identity holds, then, we have
for all pairs a, b of elements of R, so the ring R is commutative.
. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e.
. The area of the shaded part can be found by adding the areas of the two rectangles; 
, which can be factorized to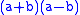 
. Therefore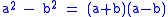 
Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is
. A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is 
and whose height is 
. This rectangle's area is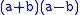 
. Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, 
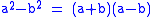.Any odd number can be expressed as difference of two squares.
coefficients.
For example, the root of
can be found using difference of two squares:
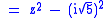
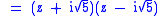
Therefore the linear factors are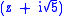
and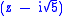 
.
of irrational
denominators. This is a method for removing surds
from expressions (or at least moving them), applying to division by some combinations involving square root
s.
For example:
The denominator of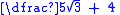
can be rationalised as follows:
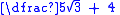
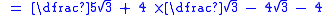
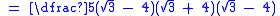
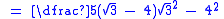
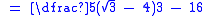
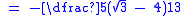
Here, the irrational denominator
has been rationalised to 
.
Any odd number can be expressed as difference of two squares.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number. It refers to the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
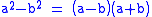
from elementary algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Proof
The proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
is straightforward, starting from the RHS
Sides of an equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...
: apply the distributive law to get a sum of four terms, and set as an application of the commutative law. The resulting identity is one of the most commonly used in all of mathematics.
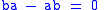
The proof just given indicates the scope of the identity in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
: it will hold in any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R.
Also, conversely, if this identity holds in a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R for all pairs of elements a and b of the ring, then R is commutative. To see this, we apply the distributive law to the right-hand side of the original equation and get
and if this is equal to
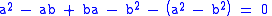
, then we haveand by associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and the rule that
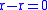, we can rewrite this asIf the original identity holds, then, we have
for all pairs a, b of elements of R, so the ring R is commutative.In geometry
The difference of two squares can also be illustrated geometrically as the difference of two square areas in a planePlane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e.
. The area of the shaded part can be found by adding the areas of the two rectangles; , which can be factorized to 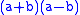. Therefore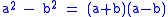 Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is
. A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is and whose height is . This rectangle's area is 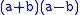. Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, 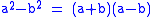.Any odd number can be expressed as difference of two squares.Complex number case: sum of two squares
The difference of two squares is used to find the linear factors of the sum of two squares, using complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients.
For example, the root of
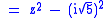
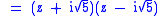
can be found using difference of two squares:Therefore the linear factors are
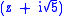and 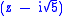.Rationalising denominators
The difference of two squares can also be used in the rationalisingRationalisation (mathematics)
In elementary algebra, root rationalisation is a process by which surds in the denominator of an irrational fraction are eliminated.These surds may be monomials or binomials involving square roots, in simple examples...
of irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
denominators. This is a method for removing surds
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
from expressions (or at least moving them), applying to division by some combinations involving square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s.
For example:
The denominator of
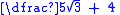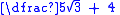
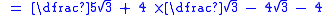
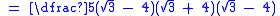
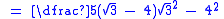
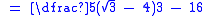
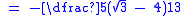
can be rationalised as follows:Here, the irrational denominator
has been rationalised to .Any odd number can be expressed as difference of two squares.