
Automorphic number
Encyclopedia
In mathematics
an automorphic number (sometimes referred to as a circular number) is a number
whose square
"ends" in the same digits as number itself. For example, 52 = 25, 762 = 5776, and 8906252 = 793212890625, so 5, 76 and 890625 are all automorphic numbers.
The sequence of automorphic numbers begins 1, 5, 6, 25
, 76
, 376, 625, 9376, ... .
Given a k-digit automorphic number , an automorphic number
, an automorphic number  with at most 2k-digits can be found by from the formula:
with at most 2k-digits can be found by from the formula:
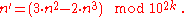
For k greater than 1, there are at most two automorphic numbers with k digit
s, one ending in 5 and one ending in 6. One of them has the form:
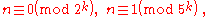
and the other has the form:
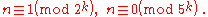
The sum of the two numbers is 10k + 1. The smaller of these two numbers may be less than 10k-1; for example with k = 4 the two numbers are 9376 and 625. In this case there is only one k digit automorphic number; the smaller number could only form a k digit automorphic number if a leading 0 were added to its digits.
The following digit sequence can be used to find the two k-digit automorphic numbers, where .
.
12781 25400 13369 00860 34889 08436 40238 75765 93682 19796
26181 91783 35204 92704 19932 48752 37825 86714 82789 05344
89744 01426 12317 03569 95484 19499 44461 06081 46207 25403
65599 98271 58835 60350 49327 79554 07419 61849 28095 20937
53026 85239 09375 62839 14857 16123 67351 97060 92242 42398
77700 75749 55787 27155 97674 13458 99753 76955 15862 71888
79415 16307 56966 88163 52155 04889 82717 04378 50802 84340
84412 64412 68218 48514 15772 99160 34497 01789 23357 96684
99144 73895 66001 93254 58276 78000 61832 98544 26232 82725
75561 10733 16069 70158 64984 22229 12554 85729 87933 71478
66323 17240 55157 56102 35254 39949 99345 60808 38011 90741
53006 00560 55744 81870 96927 85099 77591 80500 75416 42852
77081 62011 35024 68060 58163 27617 16767 65260 93752 80568
44214 48619 39604 99834 47280 67219 06670 41724 00942 34466
19781 24266 90787 53594 46166 98508 06463 61371 66384 04902
92193 41881 90958 16595 24477 86184 61409 12878 29843 84317
03248 17342 88865 72737 66314 65191 04988 02944 79608 14673
76050 39571 96893 71467 18013 75619 05546 29968 14764 26390
39530 07319 10816 98029 38509 89006 21665 09580 86381 10005
57423 42323 08961 09004 10661 99773 92256 25991 82128 90625
One automorphic number is found by taking the last k digits of this sequence; the second is found by subtracting the first number from .
.
A single digit number x is automorphic in radix b > x when b divides x2 − x. So 6 is automorphic in a radix which is a divisor of 62 − 6 = 30 that is greater than 6; these divisors are 10, 15 and 30.
In any given radix there are 2p sequences of automorphic numbers where p is the number of distinct prime factors in the radix. For base 10 this gives 22 = 4 sequences, which are 0,1,5 and 6 for 1 digit or 00, 01, 25, 76 for two digits and so on. A prime radix (such as 2,3,4,5,7,8,9,11,13,16,17,...) can only have 0 and 1 (prepended by one or more zeroes) as automorphic numbers. Base 6 is the first radix with non-trivial automorphic numbers and base 15 the first such odd radix. Base 30 is the first radix with three distinct prime factors and has 8 sequences of automorphic numbers. Here some examples of non-trivial 1,2 and 4 digit automorphic numbers in other radixes (using A-Z except I and O to represent digits 10 to 34):
Note that the base 30 numbers expressed in decimal are also automorphic in the last 4 digits.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
an automorphic number (sometimes referred to as a circular number) is a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
whose square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
"ends" in the same digits as number itself. For example, 52 = 25, 762 = 5776, and 8906252 = 793212890625, so 5, 76 and 890625 are all automorphic numbers.
The sequence of automorphic numbers begins 1, 5, 6, 25
25 (number)
25 is the natural number following 24 and preceding 26.-In mathematics:It is a square number, being 5² = 5 × 5. It is the smallest square that is also a sum of two squares: 25 = 3² + 4²...
, 76
76 (number)
76 is the natural number following 75 and preceding 77.-In mathematics:Seventy-six is a Lucas number, an automorphic number, a nontotient, a 14-gonal number, and a centered pentagonal number....
, 376, 625, 9376, ... .
Given a k-digit automorphic number
 , an automorphic number
, an automorphic number  with at most 2k-digits can be found by from the formula:
with at most 2k-digits can be found by from the formula: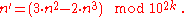
For k greater than 1, there are at most two automorphic numbers with k digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s, one ending in 5 and one ending in 6. One of them has the form:
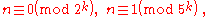
and the other has the form:
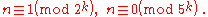
The sum of the two numbers is 10k + 1. The smaller of these two numbers may be less than 10k-1; for example with k = 4 the two numbers are 9376 and 625. In this case there is only one k digit automorphic number; the smaller number could only form a k digit automorphic number if a leading 0 were added to its digits.
The following digit sequence can be used to find the two k-digit automorphic numbers, where
 .
.12781 25400 13369 00860 34889 08436 40238 75765 93682 19796
26181 91783 35204 92704 19932 48752 37825 86714 82789 05344
89744 01426 12317 03569 95484 19499 44461 06081 46207 25403
65599 98271 58835 60350 49327 79554 07419 61849 28095 20937
53026 85239 09375 62839 14857 16123 67351 97060 92242 42398
77700 75749 55787 27155 97674 13458 99753 76955 15862 71888
79415 16307 56966 88163 52155 04889 82717 04378 50802 84340
84412 64412 68218 48514 15772 99160 34497 01789 23357 96684
99144 73895 66001 93254 58276 78000 61832 98544 26232 82725
75561 10733 16069 70158 64984 22229 12554 85729 87933 71478
66323 17240 55157 56102 35254 39949 99345 60808 38011 90741
53006 00560 55744 81870 96927 85099 77591 80500 75416 42852
77081 62011 35024 68060 58163 27617 16767 65260 93752 80568
44214 48619 39604 99834 47280 67219 06670 41724 00942 34466
19781 24266 90787 53594 46166 98508 06463 61371 66384 04902
92193 41881 90958 16595 24477 86184 61409 12878 29843 84317
03248 17342 88865 72737 66314 65191 04988 02944 79608 14673
76050 39571 96893 71467 18013 75619 05546 29968 14764 26390
39530 07319 10816 98029 38509 89006 21665 09580 86381 10005
57423 42323 08961 09004 10661 99773 92256 25991 82128 90625
One automorphic number is found by taking the last k digits of this sequence; the second is found by subtracting the first number from
 .
.Other radixes
Automorphic numbers are radix dependent, and the description above applies to automorphic numbers in base 10. Using other radixes there are different automorphic numbers. 0 and 1 are automorphic numbers in any radix; automorphic numbers other than 0 and 1 only exist when the radix has at least two distinct prime factors.A single digit number x is automorphic in radix b > x when b divides x2 − x. So 6 is automorphic in a radix which is a divisor of 62 − 6 = 30 that is greater than 6; these divisors are 10, 15 and 30.
In any given radix there are 2p sequences of automorphic numbers where p is the number of distinct prime factors in the radix. For base 10 this gives 22 = 4 sequences, which are 0,1,5 and 6 for 1 digit or 00, 01, 25, 76 for two digits and so on. A prime radix (such as 2,3,4,5,7,8,9,11,13,16,17,...) can only have 0 and 1 (prepended by one or more zeroes) as automorphic numbers. Base 6 is the first radix with non-trivial automorphic numbers and base 15 the first such odd radix. Base 30 is the first radix with three distinct prime factors and has 8 sequences of automorphic numbers. Here some examples of non-trivial 1,2 and 4 digit automorphic numbers in other radixes (using A-Z except I and O to represent digits 10 to 34):
| number of digits (n) | radix | numbers formed by last n digits | expressed in decimal |
|---|---|---|---|
| 1 | 6 | 3,4 | |
| 2 | 6 | 13,44 | 9, 28 |
| 4 | 6 | 0213,5344 | 81, 1216 |
| 1 | 10 | 5,6 | |
| 2 | 10 | 25,76 | |
| 4 | 10 | 0625,9376 | |
| 1 | 12 | 4,9 | |
| 2 | 12 | 54,69 | 64, 81 |
| 3 | 12 | 854,369 | 1216, 513 |
| 4 | 12 | 3854,8369 | 6400, 14337 |
| 1 | 14 | 7,8 | |
| 2 | 14 | 37,A8 | 49, 148 |
| 4 | 14 | 0C37,D1A8 | 2401, 344 |
| 1 | 15 | 6,A | 6,10 |
| 2 | 15 | 86,6A | 126, 100 |
| 1 | 18 | 9,A | 9, 10 |
| 2 | 18 | 49,DA | 81, 244 |
| 4 | 18 | 1249,GFDA | 6561, 98416 |
| 1 | 24 Base 24 The base- system is a numeral system with 24 as its base.There are 24 hours in a nychthemeron , so solar time includes a base-24 component.See also base 12. Decimal Equivalent... |
9,G | 9, 16 |
| 2 | 24 | M9,2G | 513, 64 |
| 4 | 24 | D0M9,AP2G | 180225, 151552 |
| 1 | 30 Base 30 Base 30 or trigesimal is a positional numeral system using 30 as the radix. Digits in this base can be represented using the Arabic numerals 0-9 and the Latin letters A-T.... |
6,A,F,G,M,R | 6, 10, 15, 16, 21, 25 |
| 2 | 30 | K6,3A,7F,NG,SM,AR | 576, 100, 225, 676, 801, 325 |
| 4 | 30 | B2K6,H13A,1S7F,U3NG,CUSM,JTAR | 299376, 460000, 50625, 759376, 350001, 510625 |
Note that the base 30 numbers expressed in decimal are also automorphic in the last 4 digits.

