In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the simplest form of the parallelogram law (also called the parallelogram identity) belongs to elementary geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

. It states that the sum of the squares of the lengths of the four sides of a parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

 equals the sum of the squares of the lengths of the two diagonals. Using the notation in the diagram on the right, the sides are (AB), (BC), (CD), (DA). But since in Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

 a parallelogram necessarily has opposite sides equal, or (AB) = (CD) and (BC) = (DA), the law can be stated as,

In case the parallelogram is a rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

, the two diagonals are of equal lengths (AC) = (BD) so,

and the statement reduces to the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

. For the general quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

 with four sides not necessarily equal,

where x is the length of the line joining the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

s of the diagonals. It can be seen from the diagram that, for a parallelogram, then x = 0 and the general formula reduces to the parallelogram law.

The parallelogram law in inner product spaces

In a normed space, the statement of the parallelogram law is an equation relating norms

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

:


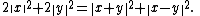
In an inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

, the norm is determined using the inner product:


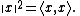
As a consequence of this definition, in an inner product space the parallelogram law is an algebraic identity, readily established using the properties of the inner product:


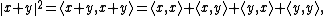
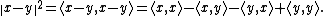
Adding these two expressions:


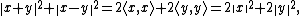
as required.

If x is orthogonal to y, then and the above equation for the norm of a sum becomes: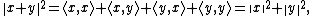


which is Pythagoras' theorem.

Normed vector spaces satisfying the parallelogram law

Most real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 and complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 normed vector space

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

s do not have inner products, but all normed vector spaces have norms (by definition). For example, a commonly used norm is the p-norm:


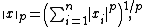
where the 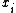are the components of vector .

Given a norm, one can evaluate both sides of the parallelogram law above. A remarkable fact is that if the parallelogram law holds, then the norm must arise in the usual way from some inner product. In particular, it holds for the p-norm if and only if p = 2, the so-called Euclidean norm or standard norm.

For any norm satisfying the parallelogram law (which necessarily is an inner product norm), the inner product generating the norm is unique as a consequence of the polarization identity

Polarization identity

In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...

. In the real case, the polarization identity is given by:


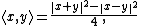
or, equivalently, by:


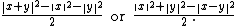
In the complex case it is given by:


For example, using the p-norm with p = 2 and real vectors 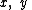, the evaluation of the inner product proceeds as follows: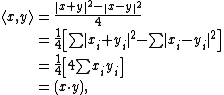


which is the standard dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

 of two vectors.

External links

• The Parallelogram Law Proven Simply at UNLV Kappa Sigma
• The Parallelogram Law: A Proof Without Words at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Proof of Parallelogram Law at Planet Math