
Polygonal number
Encyclopedia
In mathematics
, a polygonal number is a number
represented as dots or pebbles arranged in the shape of a regular polygon
. The dots were thought of as alphas (units). These are one type of 2-dimensional figurate number
s.
(see triangular number
):
But 10 cannot be arranged as a square
. The number 9, on the other hand, can be (see square number
):
Some numbers, like 36, can be arranged both as a square and as a triangle (see square triangular number
):
By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.
Triangular numbers
Square numbers
Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.
Pentagonal numbers
Hexagonal numbers
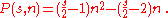
The nth s-gonal number is also related to the triangular numbers Tn as follows:

Thus:
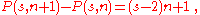
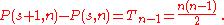
For a given s-gonal number P(s,n) = x, one can find n by
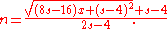
The On-Line Encyclopedia of Integer Sequences
eschews terms using Greek prefixes (e.g., "octagonal") in favor of terms using numerals (i.e., "8-gonal").
. The simplest example of this is the sequence of square triangular number
s.
The following table summarizes the set of s-gonal t-gonal numbers for small values of s and t.
In some cases, such as s=10 and t=4, there are no numbers in both sets other than 1.
The problem of finding numbers that belong to three polygonal sets is more difficult. A computer search for pentagonal square triangular numbers has yielded only the trivial value of 1, though a proof that there are no such number has yet to appear in print. All hexagonal square numbers are also hexagonal square triangular numbers, and 1225 is actually a hecticositetragonal, hexacontagonal, icosinonagonal, hexagonal, square, triangular number.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a polygonal number is a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
represented as dots or pebbles arranged in the shape of a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
. The dots were thought of as alphas (units). These are one type of 2-dimensional figurate number
Figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...
s.
Definition and examples
The number 10, for example, can be arranged as a triangleTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
(see triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
):
          |
But 10 cannot be arranged as a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. The number 9, on the other hand, can be (see square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
):
         |
Some numbers, like 36, can be arranged both as a square and as a triangle (see square triangular number
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
):
                                    |
                                    |
By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.
Triangular numbers
Square numbers
Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.
Pentagonal numbers
Hexagonal numbers
Formulae
If s is the number of sides in a polygon, the formula for the nth s-gonal number P(s,n) is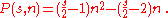
The nth s-gonal number is also related to the triangular numbers Tn as follows:

Thus:
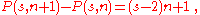
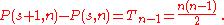
For a given s-gonal number P(s,n) = x, one can find n by
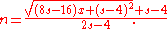
Table of values
| s | Name | Formula | n=1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Sum of Reciprocals | OEIS On-Line Encyclopedia of Integer Sequences The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs... number |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | Triangular Triangular number A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n... |
½(1n² + 1n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 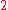 |
|
| 4 | Square Square number In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself... |
½(2n² - 0n) | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 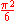 |
|
| 5 | Pentagonal Pentagonal number A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical... |
½(3n² - 1n) | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | 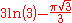 |
|
| 6 | Hexagonal Hexagonal number A hexagonal number is a figurate number. The nth hexagonal number will be the number of points in a hexagon with n regularly spaced points on a side.The formula for the nth hexagonal number... |
½(4n² - 2n) | 1 | 6 | 15 | 28 | 45 | 66 | 91 | 120 | 153 | 190 | 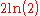 |
|
| 7 | Heptagonal | ½(5n² - 3n) | 1 | 7 | 18 | 34 | 55 | 81 | 112 | 148 | 189 | 235 | 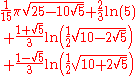 |
|
| 8 | Octagonal | ½(6n² - 4n) | 1 | 8 | 21 | 40 | 65 | 96 | 133 | 176 | 225 | 280 | 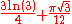 |
|
| 9 | Nonagonal | ½(7n² - 5n) | 1 | 9 | 24 | 46 | 75 | 111 | 154 | 204 | 261 | 325 | ||
| 10 | Decagonal Decagonal number A decagonal number is a figurate number that represents a decagon. The n-th decagonal number is given by the formulaThe first few decagonal numbers are:... |
½(8n² - 6n) | 1 | 10 | 27 | 52 | 85 | 126 | 175 | 232 | 297 | 370 | 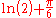 |
|
| 11 | Hendecagonal | ½(9n² - 7n) | 1 | 11 | 30 | 58 | 95 | 141 | 196 | 260 | 333 | 415 | ||
| 12 | Dodecagonal | ½(10n² - 8n) | 1 | 12 | 33 | 64 | 105 | 156 | 217 | 288 | 369 | 460 | ||
| 13 | Tridecagonal | ½(11n² - 9n) | 1 | 13 | 36 | 70 | 115 | 171 | 238 | 316 | 405 | 505 | ||
| 14 | Tetradecagonal | ½(12n² - 10n) | 1 | 14 | 39 | 76 | 125 | 186 | 259 | 344 | 441 | 550 | 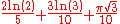 |
|
| 15 | Pentadecagonal | ½(13n² - 11n) | 1 | 15 | 42 | 82 | 135 | 201 | 280 | 372 | 477 | 595 | ||
| 16 | Hexadecagonal | ½(14n² - 12n) | 1 | 16 | 45 | 88 | 145 | 216 | 301 | 400 | 513 | 640 | ||
| 17 | Heptadecagonal | ½(15n² - 13n) | 1 | 17 | 48 | 94 | 155 | 231 | 322 | 428 | 549 | 685 | ||
| 18 | Octadecagonal | ½(16n² - 14n) | 1 | 18 | 51 | 100 | 165 | 246 | 343 | 456 | 585 | 730 | ||
| 19 | Nonadecagonal | ½(17n² - 15n) | 1 | 19 | 54 | 106 | 175 | 261 | 364 | 484 | 621 | 775 | ||
| 20 | Icosagonal | ½(18n² - 16n) | 1 | 20 | 57 | 112 | 185 | 276 | 385 | 512 | 657 | 820 | ||
| 21 | Icosihenagonal | ½(19n² - 17n) | 1 | 21 | 60 | 118 | 195 | 291 | 406 | 540 | 693 | 865 | ||
| 22 | Icosidigonal | ½(20n² - 18n) | 1 | 22 | 63 | 124 | 205 | 306 | 427 | 568 | 729 | 910 | ||
| 23 | Icositrigonal | ½(21n² - 19n) | 1 | 23 | 66 | 130 | 215 | 321 | 448 | 596 | 765 | 955 | ||
| 24 | Icositetragonal | ½(22n² - 20n) | 1 | 24 | 69 | 136 | 225 | 336 | 469 | 624 | 801 | 1000 |
The On-Line Encyclopedia of Integer Sequences
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
eschews terms using Greek prefixes (e.g., "octagonal") in favor of terms using numerals (i.e., "8-gonal").
Combinations
Some numbers, such as 36 which is both square and triangular, fall into two polygonal sets. The problem of determining, given two such sets, all numbers that belong to both can be solved by reducing the problem to Pell's equationPell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
. The simplest example of this is the sequence of square triangular number
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
s.
The following table summarizes the set of s-gonal t-gonal numbers for small values of s and t.
| s | t | Sequence | OEIS On-Line Encyclopedia of Integer Sequences The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs... number |
|---|---|---|---|
| 4 | 3 | 1, 36, 1225, 41616, … | |
| 5 | 3 | 1, 210, 40755, 7906276, … | |
| 5 | 4 | 1, 9801, 94109401, … | |
| 6 | 3 | All hexagonal numbers are also triangular. | |
| 6 | 4 | 1, 1225, 1413721, 1631432881, … | |
| 6 | 5 | 1, 40755, 1533776805, … | |
| 7 | 3 | 1, 55, 121771, 5720653, … | |
| 7 | 4 | 1, 81, 5929, 2307361, … | |
| 7 | 5 | 1, 4347, 16701685, 64167869935, … | |
| 7 | 6 | 1, 121771, 12625478965, … | |
| 8 | 3 | 1, 21, 11781, 203841, … | |
| 8 | 4 | 1, 225, 43681, 8473921, … | |
| 8 | 5 | 1, 176, 1575425, 234631320, … | |
| 8 | 6 | 1, 11781, 113123361, … | |
| 8 | 7 | 1, 297045, 69010153345, … | |
| 9 | 3 | 1, 325, 82621, 20985481, … | |
| 9 | 4 | 1, 9, 1089, 8281, 978121, … | |
| 9 | 5 | 1, 651, 180868051, … | |
| 9 | 6 | 1, 325, 5330229625, … | |
| 9 | 7 | 1, 26884, 542041975, … | |
| 9 | 8 | 1, 631125, 286703855361, … |
In some cases, such as s=10 and t=4, there are no numbers in both sets other than 1.
The problem of finding numbers that belong to three polygonal sets is more difficult. A computer search for pentagonal square triangular numbers has yielded only the trivial value of 1, though a proof that there are no such number has yet to appear in print. All hexagonal square numbers are also hexagonal square triangular numbers, and 1225 is actually a hecticositetragonal, hexacontagonal, icosinonagonal, hexagonal, square, triangular number.

