Relational quantum mechanics - AbsoluteAstronomy.com

This article is intended for those already familiar with quantum mechanics and its attendant interpretational difficulties. Readers who are new to the subject may first want to read the introduction to quantum mechanics
Introduction to quantum mechanics
Quantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....

.

Relational quantum mechanics (RQM) is an interpretation of quantum mechanics

Interpretation of quantum mechanics

An interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics informs our understanding of nature. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations...

which treats the state of a quantum system as being observer-dependent, that is, the state is the relation between the observer and the system. This interpretation was first delineated by Carlo Rovelli

Carlo Rovelli

Carlo Rovelli is an Italian physicist who has worked in Italy, the USA, and France. His work is mainly in the field of quantum gravity. He is among the founders of the Loop Quantum Gravity theory.-Life and career:...

in a 1994 preprint

Preprint

A preprint is a draft of a scientific paper that has not yet been published in a peer-reviewed scientific journal.-Role:Publication of manuscripts in a peer-reviewed journal often takes weeks, months or even years from the time of initial submission, because manuscripts must undergo extensive...

, and has since been expanded upon by a number of theorists. It is inspired by the key idea behind Special Relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

, that the details of an observation

Observation

Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...

depend on the reference frame

Reference frame

Reference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...

of the observer, and uses some ideas from Wheeler

John Archibald Wheeler

John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...

on quantum information

Quantum information

In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...

.

The physical content of the theory is thus not to do with objects themselves, but the relations between them. As Rovelli puts it: "Quantum mechanics is a theory about the physical description of physical systems relative to other systems, and this is a complete description of the world".

The essential idea behind RQM is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may appear to be in a superposition

Quantum superposition

Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...

of two or more states. Consequently, if quantum mechanics is to be a complete

Completeness

In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...

theory, RQM argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation

Correlation

In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....

, between the system and its observer(s). The state vector

State vector

*A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of freedom for motion *A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of...

of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

in the observer, with respect to the observed system. However, it is held by RQM that this applies to all physical objects, whether or not they are conscious

Consciousness

Consciousness is a term that refers to the relationship between the mind and the world with which it interacts. It has been defined as: subjectivity, awareness, the ability to experience or to feel, wakefulness, having a sense of selfhood, and the executive control system of the mind...

or macroscopic

Macroscopic

The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...

(all systems are quantum systems). Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. The proponents of the relational interpretation argue that the approach clears up a number of traditional interpretational difficulties with quantum mechanics, while being simultaneously conceptually elegant and ontologically parsimonious.

History and development

Relational Quantum Mechanics arose from a historical comparison of the quandaries posed by the interpretation of quantum mechanics

Interpretation of quantum mechanics

with the situation after the Lorentz transformations were formulated but before Special Relativity

Special relativity

. Rovelli felt that just as there was an "incorrect assumption" underlying the pre-relativistic interpretation of Lorentz's equations, which was corrected by Einstein's

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

derivation of them from Lorentz covariance

Lorentz covariance

In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...

and the constancy of the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

in all reference frames, so a similarly incorrect assumption underlies many attempts to make sense of the quantum formalism

Mathematical formulation of quantum mechanics

The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...

, which was responsible for many of the interpretational difficulties posed by the theory. This incorrect assumption, he said, was that of an observer-independent state of a system, and he laid out the foundations of this interpretation to try to overcome the difficulty. Since then, the idea has been expanded upon by Lee Smolin

Lee Smolin

Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...

and Louis Crane, who have both applied the concept to quantum cosmology

Quantum cosmology

In theoretical physics, quantum cosmology is a field attempting to study the effect of quantum mechanics on the formation of the universe, or its early evolution, especially just after the Big Bang...

, and the interpretation has been applied to the EPR paradox

EPR paradox

The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...

, revealing not only a peaceful co-existence between quantum mechanics and Special Relativity, but a formal indication of a completely local

Principle of locality

In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...

character to reality.

The problem of the observer observed

This problem was initially discussed in detail in Everett's

Hugh Everett

Hugh Everett III was an American physicist who first proposed the many-worlds interpretation of quantum physics, which he termed his "relative state" formulation....

thesis, The Theory of the Universal Wavefunction

Many-worlds interpretation

The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...

. Consider observer

, measuring the state of the quantum system

. We assume that

has complete information

Information

Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...

on the system, and that

can write down the wavefunction

Wavefunction

Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...

describing it. At the same time, there is another observer

, who is interested in the state of the entire

system, and

likewise has complete information.

To analyse this system formally, we consider a system

which may take one of two states, which we shall designate

and

, ket vectors

Bra-ket notation

Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...

in the Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

. Now, the observer

wishes to make a measurement on the system. At time

, this observer may characterize the system as follows:

where

and

are probabilities of finding the system in the respective states, and obviously add up to 1. For our purposes here, we can assume that in a single experiment, the outcome is the eigenstate

(but this can be substituted throughout, mutatis mutandis, by

). So, we may represent the sequence of event in this experiment, with observer

doing the observing, as follows:

This is observer

's description of the measurement event. Now, any measurement is also a physical interaction between two or more systems. Accordingly, we can consider the tensor product

Tensor product

In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...

Hilbert space

, where

is the Hilbert space inhabited by state vector

State vector

s describing

. If the initial state of

, some degrees of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

become correlated with the state of

after the measurement, and this correlation can take one of two values:

where the direction of the arrows in the subscripts corresponds to the outcome of the measurement that

has made on

. If we now consider the description of the measurement event by the other observer,

, who describes the combined

system, but does not interact with it, the following gives the description of the measurement event according to

, from the linearity inherent in the quantum formalism:

Thus, on the assumption (see hypothesis 2 below) that quantum mechanics is complete, the two observers

and

give different but equally correct accounts of the events

Observer-dependence of state

According to

, at

, the system

is in a determinate state, namely spin up. And, if quantum mechanics is complete, then so is his description. But, for

is not uniquely determinate, but is rather entangled

Entanglement

Entanglement may refer to:* Quantum entanglement* Orientation entanglement* Entanglement * Entanglement of polymer chains, see Reptation* Wire entanglement...

with the state of

— note that his description of the situation at

is not factorisable no matter what basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

chosen. But, if quantum mechanics is complete, then the description that

gives is also complete.

Thus the standard mathematical formulation of quantum mechanics

Mathematical formulation of quantum mechanics

allows different observers to give different accounts of the same sequence of events. There are many ways to overcome this perceived difficulty. It could be described as an epistemic limitation — observers with a full knowledge of the system, we might say, could give a complete and equivalent description of the state of affairs, but that obtaining this knowledge is impossible in practice. But whom? What makes

's description better than that of

, or vice versa? Alternatively, we could claim that quantum mechanics is not a complete theory

Completeness

, and that by adding more structure we could arrive at a universal description — the much vilified, and some would even say discredited, hidden variables

Hidden variables

Hidden variables may refer to:* Hidden variable theories, in physics a class of theories trying to explain away the statistical nature of quantum mechanics* Latent variables, in statistics, variables that are inferred from other observed variables...

approach. Yet another option is to give a preferred status to a particular observer or type of observer, and assign the epithet of correctness to their description alone. This has the disadvantage of being ad hoc

Ad hoc

Ad hoc is a Latin phrase meaning "for this". It generally signifies a solution designed for a specific problem or task, non-generalizable, and not intended to be able to be adapted to other purposes. Compare A priori....

, since there are no clearly defined or physically intuitive criteria by which this super-observer ("who can observe all possible sets of observations by all observers over the entire universe") ought to be chosen.

RQM, however, takes the point illustrated by this problem at face value. Instead of trying to modify quantum mechanics to make it fit with prior assumptions that we might have about the world, Rovelli says that we should modify our view of the world to conform to what amounts to our best physical theory of motion. Just as forsaking the notion of absolute simultaneity helped clear up the problems associated with the interpretation of the Lorentz transformations, so many of the conundra associated with quantum mechanics dissolve, provided that the state of a system is assumed to be observer-dependent — like simultaneity

Relativity of simultaneity

In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...

in Special Relativity

Special relativity

. This insight follows logically from the two main hypotheses

Hypothesis

A hypothesis is a proposed explanation for a phenomenon. The term derives from the Greek, ὑποτιθέναι – hypotithenai meaning "to put under" or "to suppose". For a hypothesis to be put forward as a scientific hypothesis, the scientific method requires that one can test it...

which inform this interpretation:

Hypothesis 1: the equivalence of systems. There is no a priori
A priori and a posteriori (philosophy)
The terms a priori and a posteriori are used in philosophy to distinguish two types of knowledge, justifications or arguments...

distinction that should be drawn between quantum and macroscopic systems. All systems are, fundamentally, quantum systems.
Hypothesis 2: the completeness of quantum mechanics. There are no hidden variables
Hidden variables
Hidden variables may refer to:* Hidden variable theories, in physics a class of theories trying to explain away the statistical nature of quantum mechanics* Latent variables, in statistics, variables that are inferred from other observed variables...

or other factors which may be appropriately added to quantum mechanics, in light of current experimental evidence.

Thus, if a state is to be observer-dependent, then a description of a system would follow the form "system S is in state x with reference to observer O" or similar constructions, much like in relativity theory. In RQM it is meaningless to refer to the absolute, observer-independent state of any system.

Information and correlation

It is generally well established that any quantum mechanical measurement

Measurement in quantum mechanics

The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....

can be reduced to a set of yes/no question

Yes-no question

In linguistics, a yes–no question, formally known as a polar question, is a question whose expected answer is either "yes" or "no". Formally, they present an exclusive disjunction, a pair of alternatives of which only one is acceptable. In English, such questions can be formed in both positive...

s or bit

Bit

A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...

s that are either 1 or 0. RQM makes use of this fact to formulate the state of a quantum system (relative to a given observer!) in terms of the physical notion of information

Information theory

Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...

developed by Claude Shannon. Any yes/no question can be described as a single bit

Bit

of information. This should not be confused with the idea of a qubit

Qubit

In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....

from quantum information theory, because a qubit can be in a superposition

Quantum superposition

of values, whilst the "questions" of RQM are ordinary binary variables

Binary numeral system

The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...

.

Any quantum measurement is fundamentally a physical interaction between the system being measured and some form of measuring apparatus. By extension, any physical interaction may be seen to be a form of quantum measurement, as all systems are seen as quantum systems in RQM. A physical interaction is seen as establishing a correlation

Correlation

between the system and the observer, and this correlation is what is described and predicted by the quantum formalism.

But, Rovelli points out, this form of correlation is precisely the same as the definition of information in Shannon's theory. Specifically, an observer O observing a system S will, after measurement, have some degrees of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

correlated with those of S. The amount of this correlation is given by log₂k bits, where k is the number of possible values which this correlation may take — the number of "options" there are.

All systems are quantum systems

All physical interactions are, at bottom, quantum interactions, and must ultimately be governed by the same rules. Thus, an interaction between two particles does not, in RQM, differ fundamentally from an interaction between a particle and some "apparatus". There is no true wave collapse

Wavefunction collapse

In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...

, in the sense in which it occurs in the Copenhagen interpretation

Copenhagen interpretation

The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...

.

Because "state" is expressed in RQM as the correlation between two systems, there can be no meaning to "self-measurement". If observer

measures system

's "state" is represented as a correlation between

and

itself cannot say anything with respect to its own "state", because its own "state" is defined only relative to another observer,

. If the

compound system does not interact with any other systems, then it will possess a clearly defined state relative to

. However, because

's measurement of

breaks its unitary evolution with respect to

will not be able to give a full description of the

system (since it can only speak of the correlation between

and itself, not its own behaviour). A complete description of the

system can only be given by a further, external observer, and so forth.

Taking the model system discussed above, if

has full information on the system, it will know the Hamiltonians

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

of both

and

, including the interaction Hamiltonian

Interaction picture

In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...

. Thus, the system will evolve entirely unitarily (without any form of collapse) relative to

, if

measures

. The only reason that

will perceive a "collapse" is because

has incomplete information on the system (specifically,

does not know its own Hamiltonian, and the interaction Hamiltonian for the measurement).

Coherence

In our system above,

may be interested in ascertaining whether or not the state of

accurately reflects the state of

. We can draw up for

an operator

Operator (physics)

In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....

, which is specified as:

with an eigenvalue of 1 meaning that

indeed accurately reflects the state of

. So there is a 0 probability of

reflecting the state of

as being

if it is in fact

,and so forth. The implication of this is that at time

can predict with certainty that the

system is in some eigenstate of

, but cannot say which eigenstate it is in, unless

itself interacts with the

system.

An apparent paradox arises when one considers the comparison, between two observers, of the specific outcome of a measurement. In the problem of the observer observed section above, let us imagine that the two experiments want to compare results. It is obvious that if the observer

has the full Hamiltonians of both

and

, he will be able to say with certainty that at time

has a determinate result for

's spin, but he will not be able to say what

's result is without interaction, and hence breaking the unitary evolution

Time evolution

Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...

of the compound system (because he doesn't know his own Hamiltonian). The distinction between knowing "that" and knowing "what" is a common one in everyday life: everyone knows that the weather will be like something tomorrow, but no-one knows exactly what the weather will be like.

But, let us imagine that

measures the spin of

, and finds it to have spin down (and note that nothing in the analysis above precludes this from happening). What happens if he talks to

, and they compare the results of their experiments?

, it will be remembered, measured a spin up on the particle. This would appear to be paradoxical: the two observers, surely, will realise that they have disparate results.

However, this apparent paradox only arises as a result of the question being framed incorrectly: as long as we presuppose an "absolute" or "true" state of the world, this would, indeed, present an insurmountable obstacle for the relational interpretation. However, in a fully relational context, there is no way in which the problem can even be coherently expressed. The consistency inherent in the quantum formalism, exemplified by the "M-operator" defined above, guarantees that there will be no contradictions between records. The interaction between

and whatever he chooses to measure, be it the

compound system or

and

individually, will be a physical interaction, a quantum interaction, and so a complete description of it can only be given by a further observer

, who will have a similar "M-operator" guaranteeing coherency, and so on out. In other words, a situation such as that described above cannot violate any physical observation, as long as the physical content of quantum mechanics is taken to refer only to relations.

Relational networks

An interesting implication of RQM arises when we consider that interactions between material systems can only occur within the constraints prescribed by Special Relativity, namely within the intersections of the light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

s of the systems: when they are spatiotemporally contiguous, in other words. Relativity tells us that objects have location only relative to other objects. By extension, a network of relations could be built up based on the properties of a set of systems, which determines which systems have properties relative to which others, and when (since properties are no longer well defined relative to a specific observer after unitary evolution breaks down for that observer). On the assumption that all interactions are local (which is backed up by the analysis of the EPR paradox presented below), one could say that the ideas of "state" and spatiotemporal contiguity are two sides of the same coin: spacetime location determines the possibility of interaction, but interactions determine spatiotemporal structure. The full extent of this relationship, however, has not yet fully been explored.

RQM and quantum cosmology

RQM conceptually forbids the possibility of an external observer. Since the assignment of a quantum state requires at least two "objects" (system and observer), which must both be physical systems, there is no meaning in speaking of the "state" of the entire universe. This is because this state would have to be ascribed to a correlation between the universe and some other physical observer, but this observer in turn would have to form part of the universe, and as was discussed above, it is impossible for an object to give a complete specification of itself. Following the idea of relational networks above, an RQM-oriented cosmology would have to account for the universe as a set of partial systems providing descriptions of one another. The exact nature of such a construction remains an open question.

Relationship with other interpretations

The only group of interpretations of quantum mechanics with which RQM is almost completely incompatible is that of hidden variables theories

Hidden variables

. RQM shares some deep similarities with other views, but differs from them all to the extent to which the other interpretations do not accord with the "relational world" put forward by RQM.

Copenhagen interpretation

RQM is, in essence, quite similar to the Copenhagen interpretation

Copenhagen interpretation

, but with an important difference. In the Copenhagen interpretation, the world is assumed to be intrinsically classical

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

in nature, and wave function collapse occurs when a quantum system interacts with macroscopic apparatus. In RQM, any interaction, be it micro or macroscopic, causes the linear

Linear

In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...

ity of Schrödinger evolution

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

to break down. RQM could recover a Copenhagen-like view of the world by assigning a privileged status (not dissimilar to a preferred frame

Preferred frame

In theoretical physics, a preferred or privileged frame is usually a special hypothetical frame of reference in which the laws of physics might appear to be identifiably different from those in other frames....

in relativity) to the classical world. However, by doing this one would lose sight of the key features that RQM brings to our view of the quantum world.

Hidden variables theories

Bohm's interpretation

Bohm interpretation

The de Broglie–Bohm theory, also called the pilot-wave theory, Bohmian mechanics, and the causal interpretation, is an interpretation of quantum theory. In addition to a wavefunction on the space of all possible configurations, it also includes an actual configuration, even in situations where...

of QM does not sit well with RQM. One of the explicit hypotheses in the construction of RQM is that quantum mechanics is a complete theory, that is it provides a full account of the world. Moreover, the Bohmian view seems to imply an underlying, "absolute" set of states of all systems, which is also ruled out as a consequence of RQM.

We find a similar incompatibility between RQM and suggestions such as that of Penrose

Roger Penrose

Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...

, which postulate that some process (in Penrose's case, gravitational effects) violate the linear evolution of the Schrödinger equation for the system.

Relative-state formulation

The many-worlds

Many-worlds interpretation

family of interpretations (MWI) shares an important feature with RQM, that is, the relational nature of all value assignments (that is, properties). Everett, however, maintains that the universal wavefunction

Universal wavefunction

The Universal Wavefunction or Universal Wave Function is a term introduced by Hugh Everett in his Princeton PhD thesis The Theory of the Universal Wave Function, and forms a core concept in the relative state interpretation or many-worlds interpretation of quantum mechanics...

gives a complete description of the entire universe, while Rovelli argues that this is problematic, both because this description is not tied to a specific observer (and hence is "meaningless" in RQM), and because RQM maintains that there is no single, absolute description of the universe as a whole, but rather a net of inter-related partial descriptions.

Consistent histories approach

In the consistent histories

Consistent histories

In quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology...

approach to QM, instead of assigning probabilities to single values for a given system, the emphasis is given to sequences of values, in such a way as to exclude (as physically impossible) all value assignments which result in inconsistent probabilities being attributed to observed states of the system. This is done by means of ascribing values to "frameworks", and all values are hence framework-dependent.

RQM accords perfectly well with this view. However, where the consistent histories approach does not give a full description of the physical meaning of framework-dependent value (that is it does not account for how there can be "facts" if the value of any property depends on the framework chosen). By incorporating the relational view into this approach, the problem is solved: RQM provides the means by which the observer-independent, framework-dependent probabilities of various histories are reconciled with observer-dependent descriptions of the world.

EPR and quantum non-locality

RQM provides an unusual solution to the EPR paradox

EPR paradox

The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...

. Indeed, it manages to dissolve the problem altogether, inasmuch as there is no superluminal transportation of information involved in a Bell test experiment

Bell test experiments

The Bell test experiments serve to investigate the validity of the entanglement effect in quantum mechanics by using some kind of Bell inequality...

: the principle of locality is preserved inviolate for all observers.

The problem

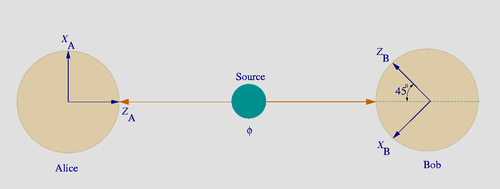
In the EPR thought experiment, a radioactive source produces two electrons in a singlet state, meaning that the sum of the spin on the two electrons is zero. These electrons are fired off at time

towards two spacelike separated observers, Alice and Bob

Alice and Bob

The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...

, who can perform spin measurements, which they do at time

. The fact that the two electrons are a singlet means that if Alice measures z-spin up on her electron, Bob will measure z-spin down on his, and vice versa: the correlation is perfect. If Alice measures z-axis spin, and Bob measures the orthogonal y-axis spin, however, the correlation will be zero. Intermediate angles give intermediate correlations in a way that, on careful analysis, proves inconsistent with the idea that each particle has a definite, independent probability of producing the observed measurements (the correlations violate Bell's inequality).

This subtle dependence of one measurement on the other holds even when measurements are made simultaneously and a great distance apart, which gives the appearance of a superluminal communication taking place between the two electrons. Put simply, how can Bob's electron "know" what Alice measured on hers, so that it can adjust its own behavior accordingly?

Relational solution

In RQM, an interaction between a system and an observer is necessary for the system to have clearly defined properties relative to that observer. Since the two measurement events take place at spacelike separation, they do not lie in the intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

of Alice' and Bob's light cone

Light cone

A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...

s. Indeed, there is no observer who can instantaneously

Relativity of simultaneity

measure both electrons' spin.

The key to the RQM analysis is to remember that the results obtained on each "wing" of the experiment only become determinate for a given observer once that observer has interacted with the other observer involved. As far as Alice is concerned, the specific results obtained on Bob's wing of the experiment are indeterminate for her, although she will know that Bob has a definite result. In order to find out what result Bob has, she has to interact with him at some time

in their future light cones.

The question then becomes one of whether the expected correlations in results will appear: will the two particles behave in accordance with the laws of quantum mechanics? Let us denote by

the idea that the observer

(Alice) measures the state of the system

(Alice's particle).

So, at time

, Alice knows the value of

: the spin of her particle, relative to herself. But, since the particles are in a singlet state, she knows that

and so if she measures her particle's spin to be

, she can predict that Bob's particle (

) will have spin

. All this follows from standard quantum mechanics, and there is no "spooky action at a distance" yet. From the "coherence-operator" discussed above, Alice also knows that if at

she measures Bob's particle and then measures Bob (that is asks him what result he got) — or vice versa — the results will be consistent:

Finally, if a third observer (Charles, say) comes along and measures Alice, Bob, and their respective particles, he will find that everyone still agrees, because his own "coherence-operator" demands that

and

while knowledge that the particles were in a singlet state tells him that

Thus the relational interpretation, by shedding the notion of an "absolute state" of the system, allows for an analysis of the EPR paradox which neither violates traditional locality constraints, nor implies superluminal information transfer, since we can assume that all observers are moving at comfortable sub-light velocities. And, most importantly, the results of every observer are in full accordance with those expected by conventional quantum mechanics.

Derivation

A promising feature of this interpretation is that RQM offers the possibility of being derived from a small number of axioms, or postulates based on experimental

Empiricism

Empiricism is a theory of knowledge that asserts that knowledge comes only or primarily via sensory experience. One of several views of epistemology, the study of human knowledge, along with rationalism, idealism and historicism, empiricism emphasizes the role of experience and evidence,...

observations. Rovelli's derivation of RQM uses three fundamental postulates. However, it has been suggested that it may be possible to reformulate the third postulate into a weaker statement, or possibly even do away with it altogether. The derivation of RQM parallels, to a large extent, quantum logic

Quantum logic

In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...

. The first two postulates are motivated entirely by experimental results

Empiricism

, while the third postulate, although it accords perfectly with what we have discovered experimentally, is introduced as a means of recovering the full Hilbert space formalism of quantum mechanics from the other two postulates. The 2 empirical postulates are:

Postulate 1: there is a maximum amount of relevant information that may be obtained from a quantum system.
Postulate 2: it is always possible to obtain new information from a system.

We let

denote the set of all possible questions that may be "asked" of a quantum system, which we shall denote by

. We may experimentally find certain relations between these questions:

, corresponding to {intersection, orthogonal sum, orthogonal complement, inclusion, and orthogonality} respectively, where

Structure

From the first postulate, it follows that we may choose a subset

mutually independent questions, where

is the number of bits contained in the maximum amount of information. We call such a question

a complete question. The value of

can be expressed as an N-tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

of binary valued numerals, which has

possible permutations of "0" and "1" values. There will also be more than one possible complete question. If we further assume that the relations

are defined for all

, then

is an orthomodular lattice, while all the possible unions of sets of complete questions form a Boolean algebra with the

as atoms.

The second postulate governs the event of further questions being asked by an observer

of a system

, when

already has a full complement of information on the system (an answer to a complete question). We denote by

the probability that a "yes" answer to a question

will follow the complete question

. If

is independent of

, then

, or it might be fully determined by

, in which case

. There is also a range of intermediate possibilities, and this case is examined below.

If the question that

wants to ask the system is another complete question,

, the probability

of a "yes" answer has certain constraints upon it:

The three constraints above are inspired by the most basic of properties of probabilities, and are satisfied if

,

where

is a unitary matrix.

Postulate 3 If and are two complete questions, then the unitary matrix associated with their probability described above satisfies the equality , for all and .

This third postulate implies that if we set a complete question

as a basis vector in a complex Hilbert space, we may then represent any other question

as a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

And the conventional probability rule of quantum mechanics states that if two sets of basis vectors are in the relation above, then the probability

Dynamics

The Heisenberg picture

Heisenberg picture

In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...

of time evolution accords most easily with RQM. Questions may be labelled by a time parameter

, and are regarded as distinct if they are specified by the same operator but are performed at different times. Because time evolution is a symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

in the theory (it forms a necessary part of the full formal derivation of the theory from the postulates), the set of all possible questions at time

is isomorphic

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

to the set of all possible questions at time

. It follows, by standard arguments in quantum logic

Quantum logic

In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...

, from the derivation above that the orthomodular lattice

has the structure of the set of linear subspace

Linear subspace

The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....

s of a Hilbert space, with the relations between the questions corresponding to the relations between linear subspaces.

It follows that there must be a unitary transformation

Unitary transformation

In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....

that satisfies:

and

where

is the Hamiltonian

Hamiltonian (quantum mechanics)

, a self-adjoint operator

Self-adjoint operator

In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...

on the Hilbert space and the unitary matrices are an abelian group

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

External links

Relational Quantum Mechanics, The Stanford Encyclopedia of Philosophy (Spring 2008 Edition)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History and development

The problem of the observer observed

Observer-dependence of state

Information and correlation

All systems are quantum systems

Coherence

Relational networks

RQM and quantum cosmology

Relationship with other interpretations

Copenhagen interpretation

Hidden variables theories

Relative-state formulation

Consistent histories approach

EPR and quantum non-locality

The problem

Relational solution

Derivation

Structure

Dynamics

See also

External links